As Equações da Reta no Espaço R³ – Geometria Analítica

Explore a matemática por trás das equações de retas no espaço tridimensional. Descubra como descrever uma reta a partir de um ponto inicial e um vetor diretor. Este artigo oferece uma visão abrangente das equações vetoriais, paramétricas e simétricas de retas, juntamente com casos especiais e exemplos resolvidos.

As equações de retas no espaço tridimensional podem parecer desafiadoras, mas são fundamentais para a geometria analítica e a física. Neste artigo, vamos desvendar os mistérios por trás das equações vetoriais, paramétricas e simétricas de retas. Vamos começar com a equação vetorial da reta, que descreve como um ponto pertence a uma reta com base em um vetor diretor. Em seguida, exploraremos as equações paramétricas, que expressam a reta em termos de um parâmetro. Além disso, abordaremos as equações simétricas e casos especiais, como retas paralelas aos eixos coordenados. Vamos simplificar essa matemática e fornecer exemplos práticos.

Para facilitar a compreensão das equações de retas no espaço tridimensional, apresentaremos exemplos práticos resolvidos. Esses exemplos abordarão diferentes cenários, como determinar a equação da reta que passa por um ponto e é paralela a um vetor dado, encontrar a interseção de duas retas, ou verificar se três pontos estão alinhados em uma reta. Cada exemplo será acompanhado de explicações passo a passo e soluções detalhadas.

A Equação Vetorial da Reta no Espaço Tridimensional

Seja r uma reta que passa pelo ponto A e tem a direção de um vetor não nulo \vec{v} . Para que um ponto do espaço P pertença à reta r , é necessário e suficiente que os vetores \vec{AP} e \vec{v} sejam colinerares como ilustrado na figura abaixo:

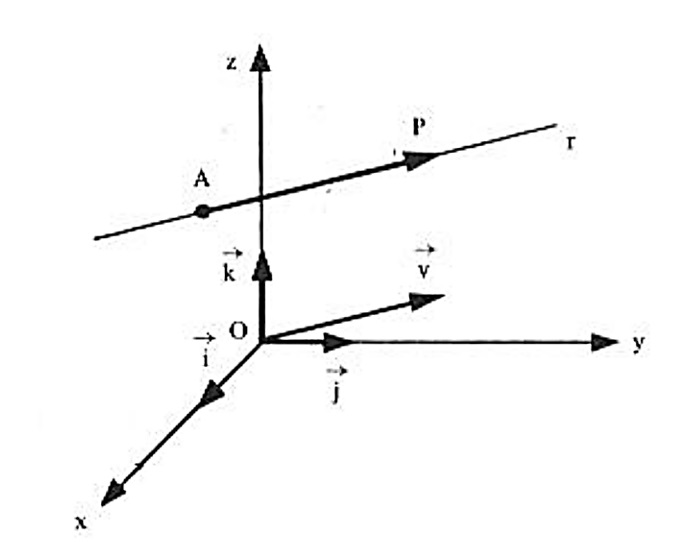
Isto é, existe t \in \mathbb{R} , tal que $$ \vec{AP} = t \vec{V} \Leftrightarrow P- A = t \vec{v} \Leftrightarrow P = A + t \vec{v}.$$ Usando as coordenadas A ( x_1 , y_1 , z_1 ) , P ( x , y , z ) e as componentes \vec{v} = ( a,b,c ) , temos que $$ P = A + t \vec{v} \Leftrightarrow (x,y,x) = ( x_1 , y_1 , z_1 ) + t (a,b,c),  \qquad t \in \mathbb{R} .$$ Qualquer uma das equações acima é denominada equação vetoria da reta r .

O vetor \vec{v} = ( a,b,c ) é chamado de vetor diretor da reta e t é chamado de parâmetro. É fácil verificar que a cada valor de t corresponde a um ponto particular P da reta.

As Equações Paramétricas da Reta no Espaço Tridimensional

Seja r uma reta que passa pelo ponto A(x_1 , y_1 , z_1) e tema direção do vetor não nulo \vec{v} = ( a , b, c ) . Sabemos que a equação vetorial da reta r é dada por $$ (x,y,z) = (x_1 , y_1 , z_1 ) + t ( a , b , c ) , \qquad t \in \mathbb{R} .$$ Daí, temos que $$ (x,y,z) = (x_1 + t 1 , y_1 + t b , z_1 + t c) $$ donde obtemos $$ \left\{ \begin{array}{rrr} x  & = & x_1 + t a \\ & \\ y &= & y_1 + t b \\  & \\ z &= & z_1 + t c \end{array} \right. ; \qquad t \in \mathbb{R} .$$ Estas equações, nas quais a, b, c não são todos nulos, são denominadas Equações Paramétricas da reta r .

A Reta Definida Por Dois Pontos

A reta definida pelos pontos A (x_1 , y_1 , z_1 ) e B (x_2 , y_2 , z_2 ) é a reta que passa pelo ponto A  ou B  e tem a direção do vetor \vec{v} = \vec{AB} = (x_2 - x_1 , y_2 - y_1 , z_2 - z_1 ). Obviamente qualque vetor múltiplo de \vec{AB} será diretor da reta determinanda pelos pontos A  e B 

As Equações Simétricas da Reta

Das equações paramétricas, supondo o produto a \cdot b \cdot c \neq 0 , e isolando o parâmetro em cada uma delas temos $$ \left\{ \begin{array}{rrr} t  & = & \frac{x – x_1}{ a } \\ & \\ t &= & \frac{y – y_1}{ b }\\  & \\ t &= & \frac{z – z_1}{ c } \end{array} \right. ; \qquad t \in \mathbb{R} .$$ Daí, temos que $$ \frac{x – x_1}{ a } = \frac{y – y_1}{b} = \frac{z – z_1}{c}.$$ Estas são denominadas equações simétricas da reta r . Elas também são chamadas de equações normais da reta que passa pelo ponto A(x_1 , y_1 , z_1) e tema direção do vetor não nulo \vec{v} = ( a , b, c ) .

Se a reta r é reta definida pelos pontos A (x_1 , y_1 , z_1 ) e B (x_2 , y_2 , z_2 ) , então suas equações simétricas são dadas por $$ \frac{x – x_1}{ x_2 – x_1 } = \frac{y – y_1}{y_2 – y_1} = \frac{z – z_1}{z_2 – z_1},$$ desde que nenhum dos denominadores seja nulo.

Condição Para o Alinhamento de três pontos:

A condição para que três pontos  A (x_1 , y_1 , z_1 ) , B (x_2 , y_2 , z_2 ) e C (x_3 , y_3 , z_3 ) estejam em linha reta é que os vetores \vec{AB} e \vec{AC} sejam colineares (ou paralelos). Isto é, se \vec{AB} = m\vec{AC} , para algum m \in \mathbb{R} . Portanto, podemos definir a condição de alinhamento entre três pontos da seguinte maneira: $$ \frac{x_3 – x_1}{ x_2 – x_1 } = \frac{y_3 – y_1}{y_2 – y_1} = \frac{z_3 – z_1}{z_2 – z_1}.$$

As Equações Reduzidas da Reta:

Às equações simétricas da reta que passa pelo ponto A(x_1 , y_1 , z_1) e tema direção do vetor não nulo \vec{v} = ( a , b, c ) , $$ \frac{x – x_1}{ a } = \frac{y – y_1}{b} = \frac{z – z_1}{c} , $$ pode-se dar outra forma isolando as variáveis y e z e expressando-as em função de x . Assim:

Desta forma, as equações $$ \left\{ \begin{array}{rrr} y  & = & mx+n \\ & \\ z &= & px + q \end{array} \right. $$ são chamadas de equações reduzidas da reta.

De forma análoga podemos expressar as equações reduzidas da reta em termos das variáveis y e z : $$ \left\{ \begin{array}{rrr} x  & = & my+n \\ & \\ z &= & py + q \end{array} \right. $$ ou $$ \left\{ \begin{array}{rrr} x  & = & mz+n \\ & \\ y &= & pz + q \end{array} \right. .$$

Equações das Retas Paralelas aos Planos e aos Eixos Coordenados

Para este nosso estudo iremos utilizar as equações paramétricas e simétricas da reta que passa pelo ponto A(x_1 , y_1 , z_1) e tema direção do vetor não nulo \vec{v} = ( a , b, c ) . Até agora, supôs-se que as componentes do vetor são diferentes de zero. Entretanto, uma ou duas destas componentes podem ser nulas. Então, temos dois casos?

1 – Uma só das componentes do vetor diretor é nula

Neste caso, o vetor \vec{v}  = (a,b,c) é ortogonal a um dos eixos coordenados e, portanto, a reta r é paralela ao plano dos outros eixos. Assim:

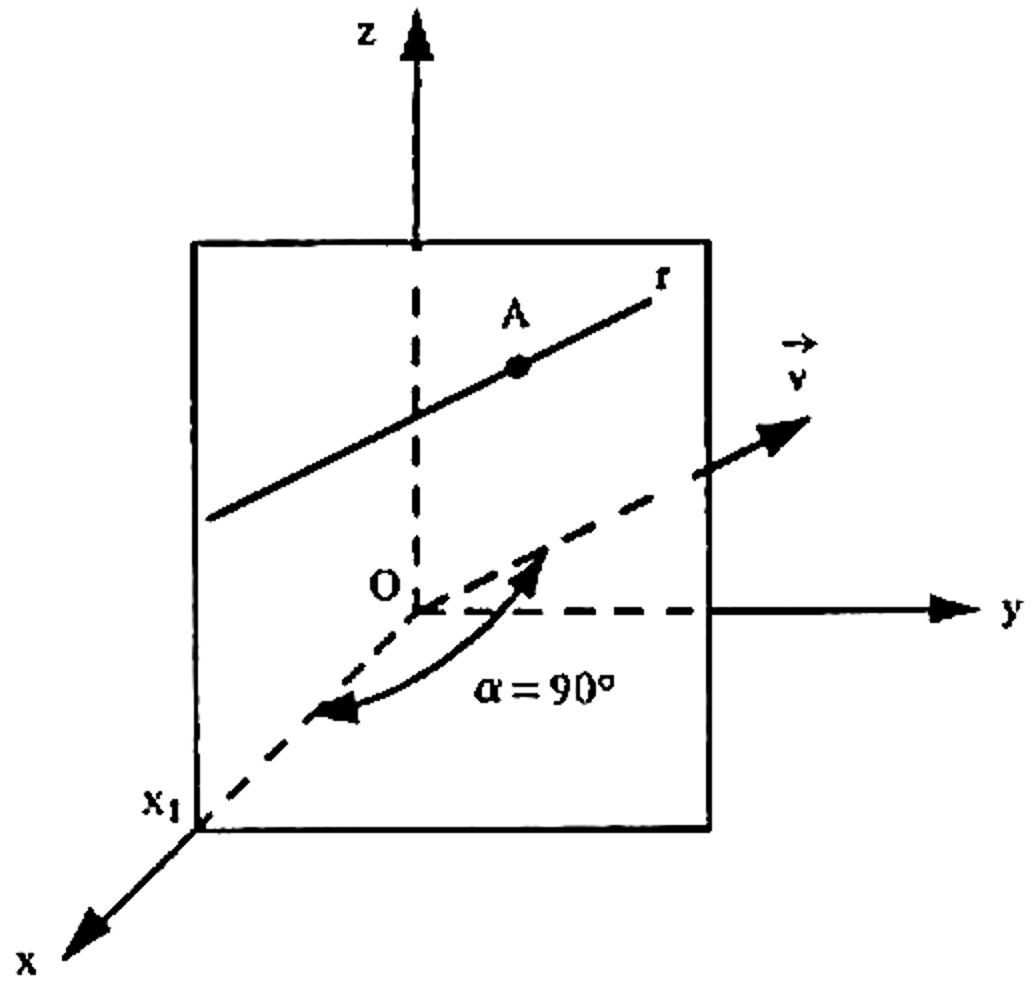
i) Se a = 0 , então \vec{v}  = (0, b, c) e a reta r é paralela ao plano yOz ;

Neste caso, as equações ficam $$ \left\{ \begin{array}{rrr} x & = & x_1 \\ & \\ \frac{y – y_1}{b} & = & \frac{z – z_1}{c} \end{array} \right. .$$ nas quais se verifica que, das coordenadas (x,y,z) de um ponto genérico P da reta r , variam somente em y e z , conservando-se que x = x_1 constante. Isso significa que a reta r se acha num plano paralelo ao plano coordenado yOz , conforme a figura abaixo.

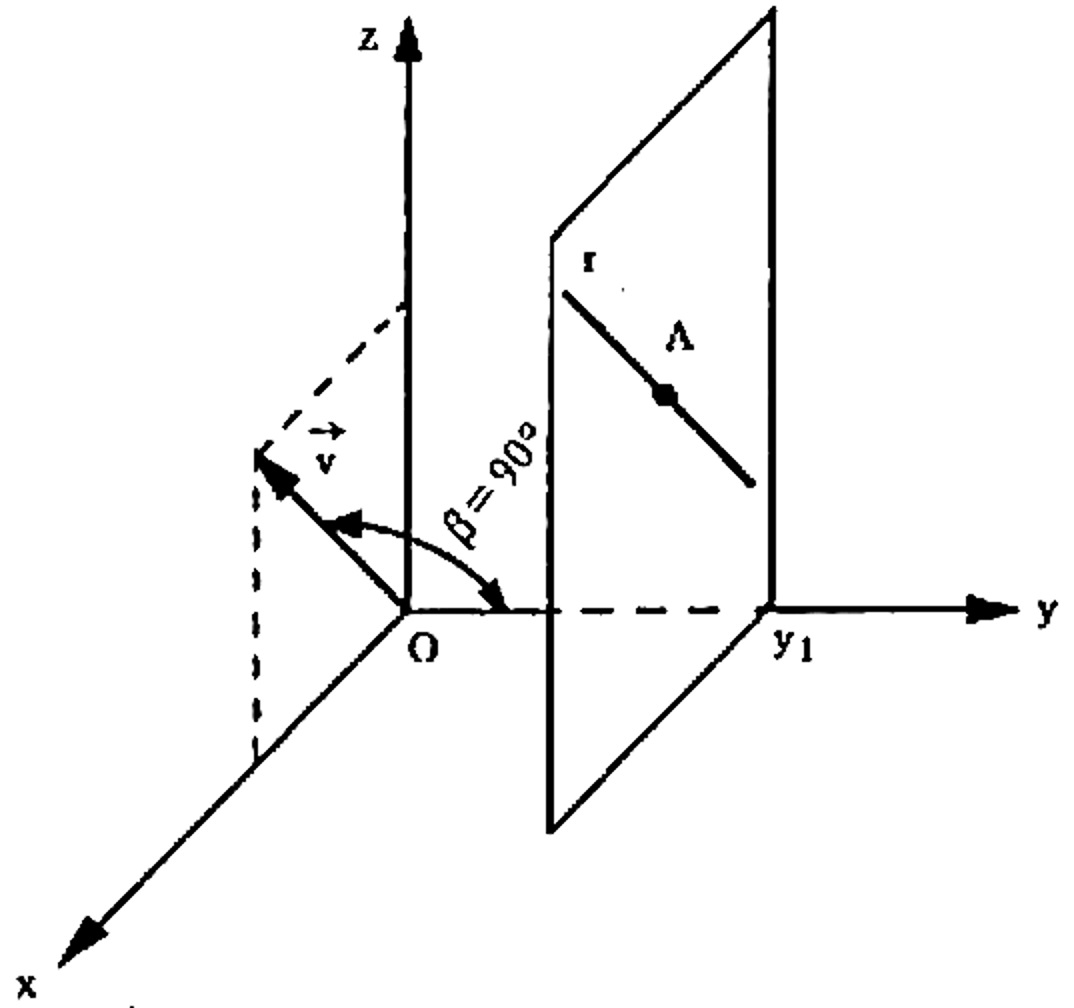
ii) Se b = 0 , então \vec{v}  = (a, 0, c) e a reta r é paralela ao plano xOz ;

Neste caso, as equações ficam $$ \left\{ \begin{array}{rrr} y & =  &y_1 \\ & \\ \frac{x – x_1}{a} & = & \frac{z – z_1}{c} \end{array} \right. $$ nas quais se verifica que, das coordenadas (x,y,z) de um ponto genérico P da reta r , variam somente em x e z , conservando-se que y = y_1 constante. Isso significa que a reta r se acha num plano paralelo ao plano coordenado xOz , conforme a figura abaixo.

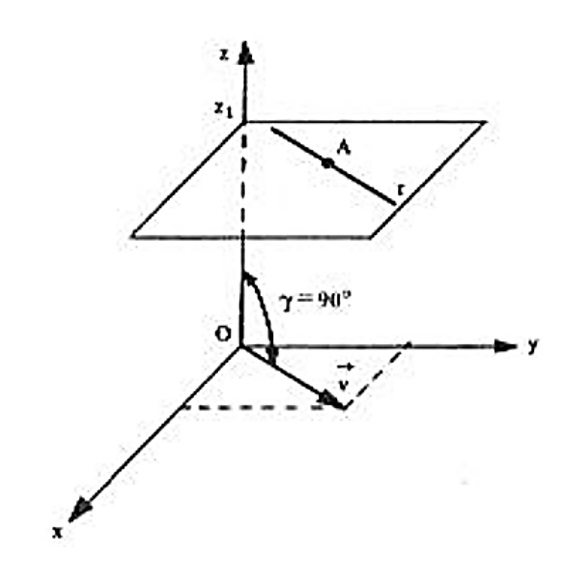
iii) Se c = 0 , então \vec{v}  = (a, b, 0) e a reta r é paralela ao plano xOy ;

Neste caso, as equações ficam $$ \left\{ \begin{array}{rrr} z & =  &z_1 \\ & \\ \frac{x – x_1}{a} & = & \frac{y – y_1}{b} \end{array} \right. $$ nas quais se verifica que, das coordenadas (x,y,z) de um ponto genérico P da reta r , variam somente em x e z , conservando-se que z = z_1 constante. Isso significa que a reta r se acha num plano paralelo ao plano coordenado xOy , conforme a figura abaixo.

2 – Duas componentes do vetor diretor são nulas

Neste caso, o vetor \vec{v}  = (a,b,c) tem a direção de um dos vetores \vec{i}  = (1,0,0) ou \vec{j}  = (0,1,0) ou \vec{k}  = (0,0,1) e, portanto, a reta r é paralela ao eixo que tem a direção de um destes vetores. Assim:

i) Se a = b = 0 , então \vec{v}  = (0, 0, c) e a reta r é paralela ao eixo Oz ;

Neste caso, as equações de r ficam $$ \left\{ \begin{array}{rrr} x & = & x_1 \\ & &  \\ y  & = & y_1 \\ & & \\ z & = &  z_1 + ct \end{array} \right. $$ e, costuma-se dizer, simplesmente, que as equações da reta r são $$ \left\{ \begin{array}{rrr} x & = & x_1 \\ & & \\ y  & = & y_1 \end{array} \right. $$

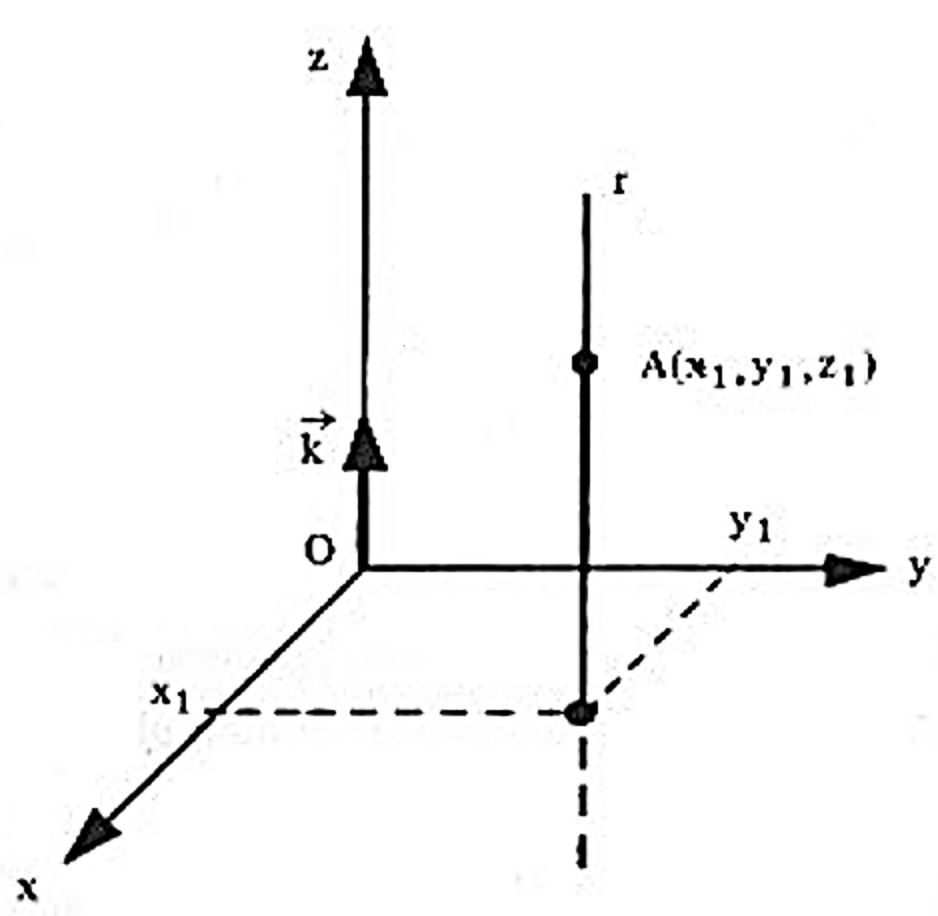
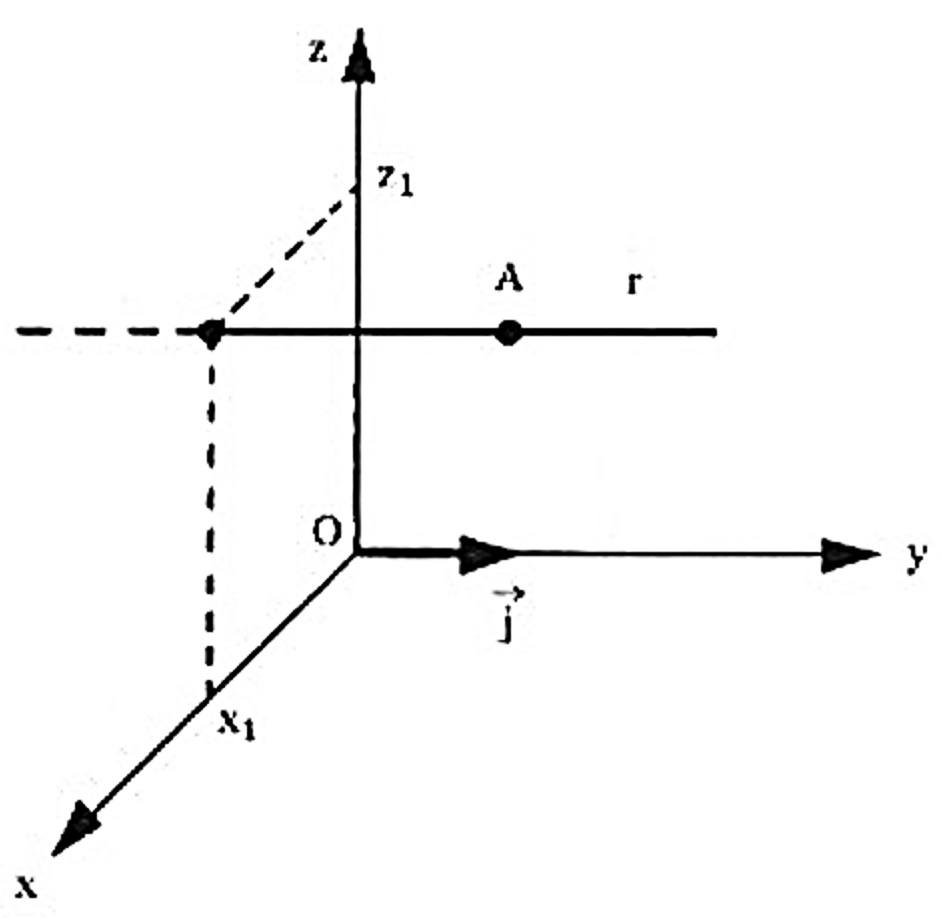
ii) Se a = c = 0 , então \vec{v}  = (0,b, 0) e a reta r é paralela ao eixo Oy ;

Neste caso, as equações de r ficam $$ \left\{ \begin{array}{rrr} x & = & x_1 \\ & &  \\ y  & = & y_1 + bt \\ & & \\ z & = &  z_1 \end{array} \right. $$ e, costuma-se dizer, simplesmente, que as equações da reta r são $$ \left\{ \begin{array}{rrr} x & = & x_1 \\ & & \\ z  & = & z_1 \end{array} \right. $$

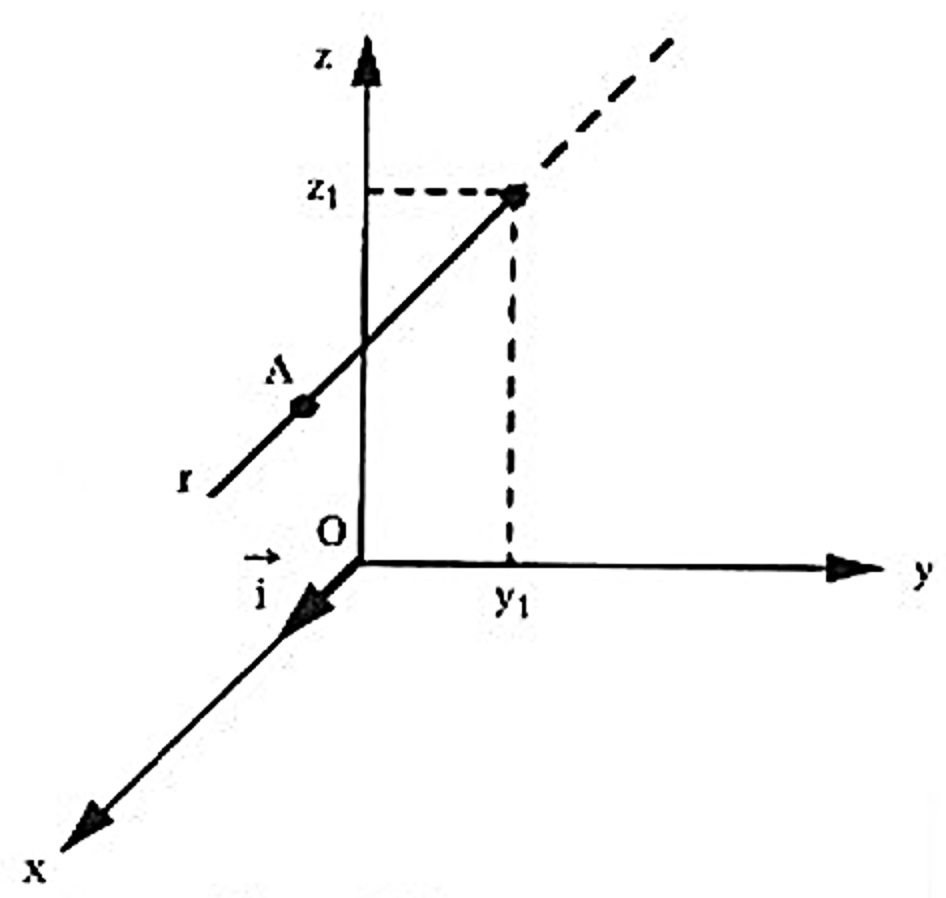
ii) Se b = c = 0 , então \vec{v}  = (a, 0, 0) e a reta r é paralela ao eixo Oz ;

Neste caso, as equações de r ficam $$ \left\{ \begin{array}{rrr} x & = & x_1 + a t \\ & &  \\ y  & = & y_1 \\ & & \\ z & = &  z_1 \end{array} \right. $$ e, costuma-se dizer, simplesmente, que as equações da reta r são $$ \left\{ \begin{array}{rrr} y & = & y_1 \\ & & \\ z  & = & z_1 \end{array} \right. $$

Observação: Os eixos Ox , Oy e Oz são retas particulares, que passam pela origem O(0,0,0) e tem a direção dos vetores \vec{i}  = (1,0,0) , \vec{j}  = (0,1,0) e \vec{k}  = (0,0,1) , respectivamente. Logo suas equações são $$ \text{Eixo Ox:  } \left\{ \begin{array}{rrr} y & = & 0 \\ & & \\ z  & = & 0\end{array} \right. $$ $$ \text{Eixo Oy:  } \left\{ \begin{array}{rrr} x & = & 0 \\ & & \\ z  & = & 0\end{array} \right. $$ $$ \text{Eixo Oz:  } \left\{ \begin{array}{rrr} x & = & 0 \\ & & \\ y  & = & 0\end{array} \right. $$

Exercícios Resolvidos

1 – Determine as equações da reta que passa pelo ponto A (3,0,-5) e tem a direção do vetor \vec{v} = (2,2,-1) :

Solução: (x,y,z) = (3,0,-5) + t (2,2,-1); \qquad t \in \mathbb{R} .

2- Determine as equações paramétricas da reta que passa pelo ponto A (3,-1, 2) e tem a direção do vetor \vec{v} = (-3, -2,1) :

Solução:  r: \left\{ \begin{array}{rrr} x  & = & 3-3t \\ & \\ y &= & -1-2t \\  & \\ z &= & 2+t \end{array} \right. ; \qquad t \in \mathbb{R} .

3 – Escreva as equações paramétricas que passa pelos pontos A (1,-2,-3) e B(3,1, -4) :

Solução: O vetor diretor desta reta é $$ \vec{AB} = B – A = (2,3,-1)$$, logo as equaçãoe paraméticas de r são r: \left\{ \begin{array}{rrr} x  & = &1+2t \\ & \\ y &= & -2 +3t\\  & \\ z &= & -3-t \end{array} \right. ; \qquad t \in \mathbb{R} .

4 – Determine as equações simétricas da reta que passa pelo ponto A(3,0,-5) e tem a direção do vetor \vec{v} = (2,2,-1) ;

Solução:  r: \dfrac{x - 3}{ 2} = \dfrac{y - 0}{2} = \dfrac{z + 5}{-1} \Leftrightarrow  r: \dfrac{x - 3}{ 2} = \dfrac{y }{2} = -z - 5 .

5 – Os pontos A(5,2,-6) ,  B(-1,-4,-3) e C(7,4,-7) estão em linha reta?

Solução: Como \dfrac{-1-5}{ 7-5} = \dfrac{-4-2}{4-2} = \dfrac{-3+6}{-7+6} então podemos afirmar que os três pontos estão em linha reta.

6 – Estabeleça as equações reduzidas da ret que passa pelos pontos A(2,1,-3) e B(4,0,-2) :

Solução: As equações simétricas da reta que passa pelo ponto A(2,1,-3) e tem a direção do vetor \vec{AB} = (2,-1,1) são : $$ r: \frac{x-2}{ 2} = \frac{y – 1}{-1} = \frac{z + 3}{1} $$ e destas equações obtém-se $$ \frac{x-2}{ 2} = \frac{z + 3}{1} \Leftrightarrow 2(y-1) = z+3\Leftrightarrow \\ \Leftrightarrow 2y – 2 = z + 3 \Leftrightarrow 2z = x -8 \Leftrightarrow z = \frac{1}{2} x – 4$$ e $$ \frac{x-2}{ 2} = \frac{y – 1}{-1} \Leftrightarrow 2(y-1) = -1(x-2) \Leftrightarrow \\ \Leftrightarrow 2y – 2 = -x +2 \Leftrightarrow 2y = -x +4 \Leftrightarrow y = -\frac{1}{2} x +2 .$$ Portanto, $$ \left\{ \begin{array}{rrr} y  & = & -\frac{1}{2} x +2 \\ & \\ z &= & \frac{1}{2} x – 4 \end{array} \right. $$ são as equações reduzidas da reta.

Conclusão:

As equações de retas no espaço tridimensional desempenham um papel fundamental na geometria analítica e em muitas aplicações práticas, incluindo física e engenharia. Este artigo explorou as equações vetoriais, paramétricas e simétricas que descrevem retas nesse espaço, juntamente com casos especiais e exemplos resolvidos. Entender essas equações é essencial para descrever movimentos, traçar trajetórias e resolver problemas geométricos em três dimensões. Com este conhecimento, os leitores terão uma base sólida para lidar com desafios matemáticos e científicos que envolvam retas no espaço tridimensional.

Leia Mais:

• Vetores no R³: O Produto Misto e Duplo Produto Vetorial
• Vetores no R³: O Produto Vetorial e suas Interpretações Geométricas
• Vetores no R³: O Produto Escalar e suas Interpretações Geométricas
• Vetores No R³: Um guia ilustrado dos vetores no espaço euclidiano