Retas e Planos nos Espaço Tridimensional: 9 Exercícios Resolvidos

Embarque em uma jornada matemática pelo espaço tridimensional! Desvendaremos equações paramétricas, planos e interseções, solucionando desafios que transformarão sua compreensão da geometria. Prepare-se para mergulhar nas profundezas da matemática espacial.

No vasto universo da geometria analítica, desvendar os segredos das retas e planos no espaço tridimensional é um desafio fascinante. Neste artigo, exploraremos exercícios resolvidos que envolvem equações paramétricas, interseções de planos e direções de vetores, conduzindo você por um caminho intrigante de descobertas matemáticas.

Retas e Planos nos Espaço Tridimensional: Exercícios Resolvidos

Ao desbravar os desafios matemáticos propostos pelos exercícios resolvidos neste artigo, a compreensão da geometria no espaço tridimensional se expande. A interconexão entre retas, planos e vetores revela a beleza e a elegância subjacentes à matemática, provando que, no universo das equações, a ordem reina supremamente.

1) Equações Paramétricas da Reta

Vamos começar determinando as equações paramétricas de uma reta que não apenas passa pela origem, mas também é perpendicular a um plano específico. A matemática por trás dessa relação nos levará a compreender a interseção entre conceitos aparentemente distintos.

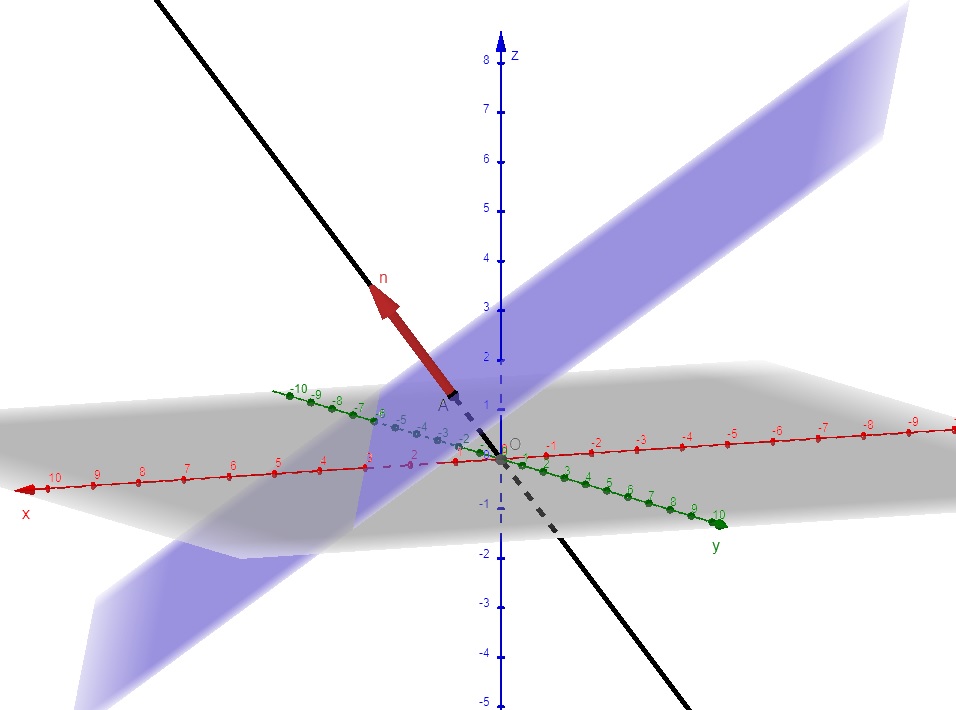
Exercício 1: Determine as equações paramétricas da reta que passa pela origem e é perpendicular ao plano de equação $$ 2x-y+3z-6 = 0.$$

Neste exercício, queremos as equações paramétricas da reta que passa pelo ponto O(0,0,0) e tem a direção do vetor normal ao plano de equação 2x-y+3z-6 = 0 . Sabemos que \vec{n} = (2,-1,3) é este vetor normal. Afinal o vetor normal ao plano e perpendicular ao plano e toda reta que tem sua direção será, também, perpendicular ao plano. Portanto, as equações paramétricas da reta que passa pela origem e é perpendicular ao plano dado é, exatamente $$ r: \left\{ \begin{array}{lll} x = 0 +2t \\ y = 0 -t \\ z = 0 + 3t \end{array} \right. = \left\{ \begin{array}{lll} x = 2t \\ y = -t \\ z = 3t \end{array} \right. .$$

2) Ponto de Interseção entre Plano e Reta

A análise continua com a determinação do ponto de interseção entre um plano definido por uma equação e uma reta com ponto inicial e vetor diretor especificados. Estaremos conectando os pontos entre teoria e aplicação prática.

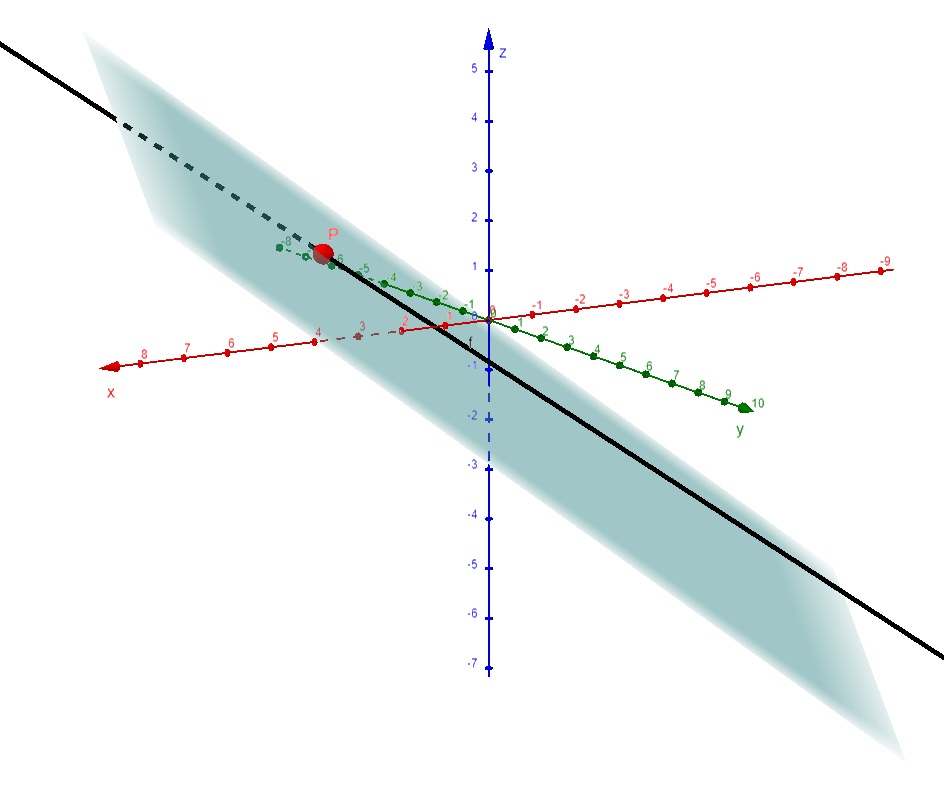
Exercício 2: Determine o ponto de interseção do plano de equação $$2x-y-3z-4 = 0$$ com a reta que passa pelo ponto A (0,1,-1) e tem a direção do vetor \vec{v} =(1,-2,1) .

Primeiramente, vamos verificar se o ponto A (0,1,-1) é um ponto do plano 2x-y-3z-4 = 0 : $$ 2 (0) -(1) – 3 (-1) – 4 = -1 +3-4 \neq 0.$$ Portanto o ponto A (0,1,-1)   não está no plano. Caso estivesse, este seria meu ponto de interseção. A forma mais simples de encontrar este ponto de interseção deste plano com a reta que passa pelo ponto A (0,1,-1) e tem a direção do vetor \vec{v} =(1,-2,1) é escrevendo as equações paramétricas da reta e depois substituindo-a no plano. Assim, $$r: \left\{ \begin{array}{lll} x = t \\ y = 1 -2 t \\ z = -1 +t \end{array} \right. $$ são equações paramétricas da reta que passa pelo ponto A (0,1,-1) e tem a direção do vetor \vec{v} =(1,-2,1) . Substituindo na equação do plano obtemos $$2 (t) – (1-2t) -3 (-1+t) -4 = 0 \Leftrightarrow t = 2.$$ Portanto, este é o valor do parâmetro t que determina o ponto do reta que também é ponto do plano. Logo, $$P(2,-3, 1) $$ é o ponto de interseção do plano de equação $$2x-y-3z-4 = 0$$ com a reta que passa pelo ponto A (0,1,-1) e tem a direção do vetor \vec{v} =(1,-2,1) .

3) Equações Paramétricas da Interseção de Planos

Agora, exploraremos as equações paramétricas de uma reta que é a interseção de dois planos distintos. Este é um mergulho profundo na complexidade matemática que envolve múltiplas variáveis e suas relações espaciais.

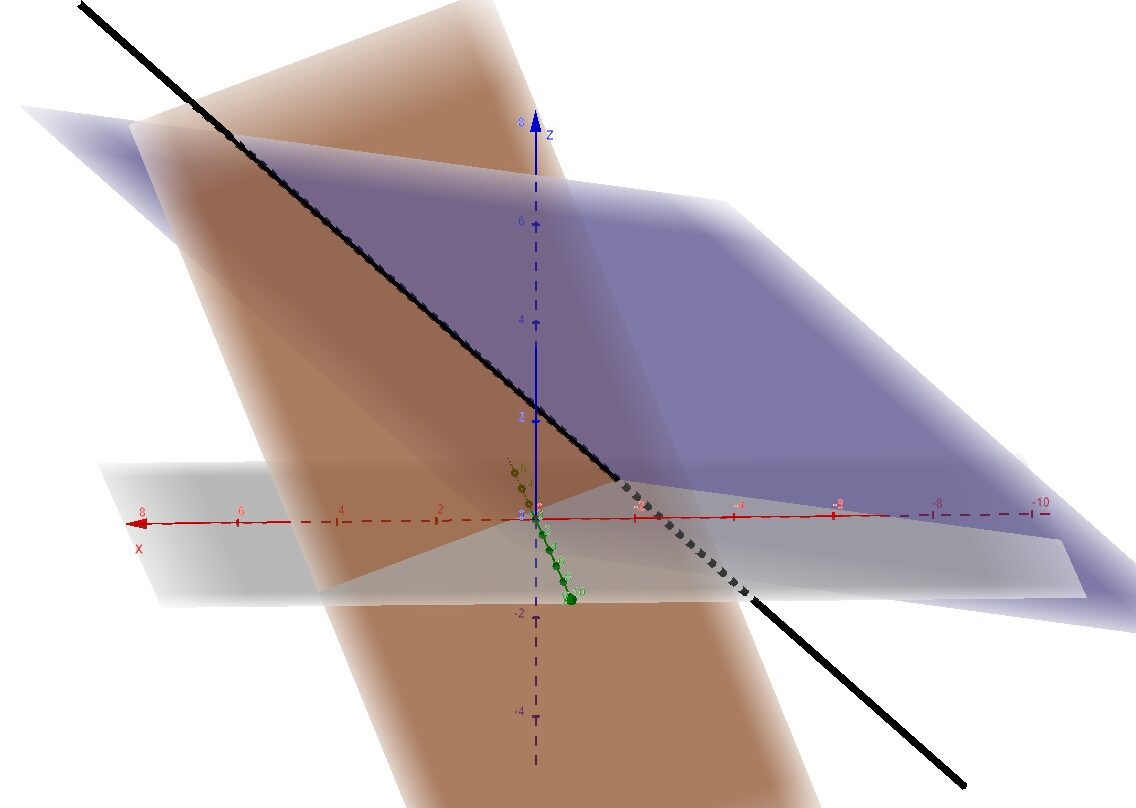
Exercício 3: Determine as equações paramétricas da reta interseção dos planos $$\pi _1 : 2x-y-z-1=0 $$ e $$\pi _2 : x+y -2z + 7 = 0.$$

Para encontrar esta reta que é a interseção dos planos $$\pi _1 : 2x-y-z-1=0 $$ e $$\pi _2 : z+y -2z + 7 = 0$$ precisamos resolver o sistema linear $$ \left\{ \begin{array}{ll} 2x-y-z = 1 \\ x+y -2z = – 7 \end{array} \right.$$ Obviamente, podemos ver que estes dois planos não são paralelos, pois seus vetores normais \vec{v_1} = (2,-1,-1) e \vec{v_2} = (1,1,-2) , respectivamente, não são paralelos, Logo, faz sentido buscar esta reta interseção. Daí, $$ \left\{ \begin{array}{ll} 2x-y-z = 1 \\ x+y -2z = – 7 \end{array} \right. \sim \left\{ \begin{array}{ll} x+y -2z = – 7 \\ 3x – 3y = -6 \end{array} \right.$$ o que nos leva a $$ x-y = -2 \Leftrightarrow x = y -2 .$$ Subtituindo esta relação na primeira equação do sistema, encontramos $$ z = y + \frac{5}{2} .$$ Assim, temos $$ r: \left\{ \begin{array}{lll} x = y -2 \\ z = y + \frac{5}{2} \end{array} \right. $$ como as equações reduzidas da reta que é interseção dos dois planos. Como queremos as equações paramétricas, faremos y = t nestas equações e obteremos $$ r: \left\{ \begin{array}{lll} x = -2 + t \\ y = t \\ z = \frac{5}{2} + t\end{array} \right. $$

4) Equação Geral do Plano Paralelo a Vetores

Desvendaremos a equação geral de um plano que não apenas passa por um ponto específico, mas também é paralelo a dois vetores dados. Este exercício ilustra como a geometria e a álgebra se entrelaçam harmoniosamente.

Exercício 4: Determine a equação geral do plano que passa pelo ponto A(-1,2,-3) e é paralelo aos vetores \vec{u} = (1,0,1) e \vec{v} = (1,1,0) .

De modo bem simples podemos encontrar o vetor normal ao plano que é paralelo aos vetores \vec{u} = (1,0,1) e \vec{v} = (1,1,0) calculando $$ \vec{n} = \vec{u} \wedge \vec{v} = \left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{array}\right| = (-1,1,1). $$ Portanto, a equação do plano que estamos procurando será dada por $$ -x+y+z+d = 0.$$ Substituindo as coordenadas do ponto A(-1,2,-3) nesta equação encontramos $$ 1 +2-3 +d = 0 \Leftrightarrow d = 0. $$ Portanto, $$ -x+y+z = 0$$ é a a equação geral do plano que passa pelo ponto A(-1,2,-3) e é paralelo aos vetores \vec{u} = (1,0,1) e \vec{v} = (1,1,0) .

5) Equação do Plano Perpendicular a Outros Dois Planos

A próxima parada nos leva a determinar a equação de um plano que não apenas passa pela origem, mas também é perpendicular a dois planos distintos. Uma exploração fascinante das relações espaciais na geometria analítica.

Exercício 5: Determine a equação geral do plano que passa pela origem e é perpendicular aos planos de equações $$ 2x-y+z-1 = 0 \qquad \text{e} \qquad x+y-2z+4=0 .$$

Um plano que seja perperdicular a dois outros planos precisa que seu vetor normal seja perpendicular aos vetores dos outros dois planos ao mesmo tempo. Logo, como \vec{n_1} = (2,-1,1) é o vetor normal ao plano de equação 2x-y+z-1 = 0 e \vec{n_2} = (1,1,-2) é o vetor normal ao plano de equação x+y-2z+4=0 . Um vetor perpendicular a estes dois vetores simultaneamente pode ser obtido fazendo $$ \vec{n} = \vec{n_1}\wedge \vec{n_2} = \left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ 2 & -1 & 1 \\ 1 & 1 & -2 \end{array}\right| = (1,5,3).$$ Portanto, como o plano passa pela origem teremos d = 0 e sua equação será $$ \pi: x +5y+3z = 0.$$

6) Plano que Passa por Dois Pontos

Aprofundaremos nossos conhecimentos ao descobrir a equação do plano que passa por dois pontos específicos e é paralelo a um vetor dado. Essa aplicação prática destaca a utilidade das ferramentas matemáticas em situações do mundo real.

Exercício 6: Determine a equação do plano que passa pelos pontos A(0,1,1) e B(2,0,-1), paralelo ao vetor $$ \vec{v} = (1,-2,3).$$

Para determinar a equação deste plano que passa pelos pontos A(0,1,1) e B(2,0,-1), paralelo ao vetor \vec{v} = (1,-2,3), basta encontrar o vetor $$ \vec{n} = \vec{AB} \wedge \vec{v} = \left| \begin{array}{ccc} \vec{i} &  \vec{j} & \vec{k} \\ 2-0 & 0-1 & -1-1 \\ 1 & -2 & 3 \end{array}  \right| = \left| \begin{array}{ccc} \vec{i} &  \vec{j} & \vec{k} \\ 2 & -1 & -2 \\ 1 & -2 & 3 \end{array}  \right| = (-7,-8,-3).$$ Desta forma, sabemos que a equação geral do plano será dada por $$ -7x-8y-3z+d = 0$$ e usando o ponto A(0,1,1), encontramos $$ -7(0)-8(1)-3(1)+d = 0 \Leftrightarrow d = 11.$$ Portanto, $$ 7x+8y+3z-11 = 0$$ é a equação geral do plano que passa pelos pontos A(0,1,1) e B(2,0,-1), paralelo ao vetor \vec{v} = (1,-2,3).

7) Determinando x em Vetores Dados

Partiremos para o desafio de determinar o valor de x, conectando vetores dados de maneiras específicas. Esse exercício não apenas testa nossas habilidades matemáticas, mas também destaca a importância da precisão nos cálculos.

Exercício 7: Determine x de forma que os vetores \vec{v_1} = (1,-1,2) , \vec{v_2} = (-1,2,1) e \vec{v_3} = (x,3,2) sejam coplanares.

Para resolver este problema devemos usar o produto misto:

• Condição de Coplanaridade: ( \vec{u} , \vec{v} , \vec{w} ) = 0 se um dos vetores é nulo, se dois deles são colineares, ou se três deles são coplanares.

Note que $$ ( \vec{v_1} , \vec{v_2} , \vec{v_3} ) = \left| \begin{array}{ccc}1 & -1 & 2 \\ -1 & 2 &  1 \\ x & 3 & 2 \end{array} \right| =0 \Leftrightarrow 4-x-6-4x-3-2 = 0 \Leftrightarrow x = – \frac{7}{5}.$$ Como este valor de x , \vec{v_3} não será colinear a nenhum dos outros dois vetores. Portanto basta que x = - \frac{7}{5} para que estes três vetores sejam coplanares.

8) Volume de um Paralelepípedo

O desenvolvimento culmina na análise do volume de um paralelepípedo formado por vetores específicos. Este exercício prático integra os conceitos anteriores em uma aplicação tridimensional tangível.

Exercício 8: Calcule o volume do paralelepípedo formado pelos vetores \vec{AB} = (1,0,1), \vec{BE} = (1,1,1) e \vec{AD} = (0,3,3).

Para resolver este problema devemos usar o produto misto:

• Geometricamente, o produto misto ( \vec{u} , \vec{v} , \vec{w} ) é igual, em módulo, ao volume do paralelepípedo de arestas determinadas pelos vetores \vec{u} = \vec{AD} , \vec{v} = \vec{AB} e \vec{w} = \vec{AC} , conforme a figura abaixo:

Observe que para o cálculo do volume precisamos que os vetores tenham a mesma origem. No nosso caso, precisamos usar o vetor $$ \vec{AE} = \vec{AB} + \vec{BE} = (1,0,1) + (1,1,1) = (2,1,2).$$ Logo, para calcular o volume do paralelepípedo formado pelos vetores \vec{AB} = (1,0,1), \vec{BE} = (1,1,1) e \vec{AD} = (0,3,3), devemos usar os vetores \vec{AB} = (1,0,1), \vec{AE} = (2,1,2) e \vec{AD} = (0,3,3), usando o produto misto $$ (\vec{AB} , \vec{AD} , \vec{AE} ) = \left| \begin{array}{ccc}1 & 0 & 1 \\ 0 & 3 &  3 \\ 2 & 1 & 2 \end{array} \right| = -3 .$$ Portanto, $$ \text{Volume do Paralelepípedo} = |-3| = 3 u.v.$$

9) Posição Relativa de Retas e Planos

Concluiremos nossa jornada estudando a posição relativa de duas entidades matemáticas: uma reta definida por uma equação paramétrica e um sistema de dois planos. Este é o ponto em que a teoria se encontra com a prática.

Exercício 9: Estude a posição relativa das retas $$ r: (x,y,z) = (1,2,3)+ t (0,1,3) \qquad \text{e} \qquad s: \left\{ \begin{array}{lll} x+y+z = 6 \\ x-y-z = -4 \end{array} \right. $$

O vetor \vec{v} = (0,1,3) é paralelo a reta r . Para determinar um vetor \vec{u} paralelo a s , tomemos dois pontos de s : fazendo z = 0 nas equações de s , obtemos x=1 e y = 5 ; fazendo z = 1 , obtemos x=1 e y=4 ; logo, B(1,5,0) e C(1,4,1) são pontos de s e portanto \vec{u} = \vec{BC} = (0,-1,1) é um vetor diretor de s . Uma outra forma de encontrar um vetor diretor desta reta é encontrando o vetor que é perpendicuar aos dois vetores normais aos planos que determinam a reta s : $$ \vec{w} = \left| \begin{array}{ccc} \vec{i} &  \vec{j} & \vec{k} \\ 1 & 1 & 1 \\ 1 & -1 & -1 \end{array}  \right| = (0,2,-2) $$ Perceba que \vec{u} e \vec{w} são vetores múltiplos, logo colineares. Como os vetores \vec{v} = (0,1,3) e \vec{u} (0,-1,1) não são múltiplos, logo não são paralelos. Assim as retas não são paralelas. Tomemos o ponto A(1,2,3) \in r e B(1,5,0) \in s. Logo, temos o vetor \vec{AB} = (0,3,-3) como vetor entre pontos da duas retas. Usando o produto misto, temos que $$ (\vec{AB} , \vec{AD} , \vec{AE} ) = \left| \begin{array}{ccc} 0& 1 & 3 \\ 0 & -1 &  1 \\ 0 & 3 & -3\end{array} \right| = 0 .$$Portanto, as duas retas são coplanares e como não são paralelas, as duas retas são concorrentes.

Leia Mais:

• Estudo do Plano: Equações Geral e Vetorial – Geometria Analítica Espacial
• Posições Relativas entre Planos e Retas no Espaço Tridimensional R³
• Retas no Espaço Euclidiano R³: Posiçoes Relativas Entre Retas.
• As Equações da Reta no Espaço R³ – Geometria Analítica
• Vetores no R³: O Produto Misto e Duplo Produto Vetorial