Retas no Espaço Euclidiano R³: Posiçoes Relativas Entre Retas.

Entre no mundo da geometria das retas no espaço \mathbb{R}^3 ! Este artigo revela as posições relativas entre elas, desmistificando conceitos e apresentando exemplos práticos. Prepare-se para uma jornada fascinante pelo plano geométrico e descubra como as retas podem se entrelaçar de formas surpreendentes.

Na vastidão tridimensional do espaço, as retas desenham um cenário intrigante de interações. Descubra conosco as posições relativas que moldam a geometria analítica, desde as paralelas que mantêm distância constante até as concorrentes que se entrelaçam em pontos únicos, passando pelas retas reversas que não são parelas nem concorrentes. Explore o fascinante universo das retas e desvende os segredos por trás de suas coincidências e divergências.

Retas Paralelas: A Condição de Paralelismo Entre Duas Retas

A condição de paralelismo das retas r_1 e r_2 é a mesma dos vetores \vec{v_1} = (a_1 , b_1 , c_1 ) e \vec{v_2} = (a_2 , b_2 , c_2 ) , que definem as direções dessas retas, isto é $$ \vec{v_1} = m \vec{v_2}$$ ou $$ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} $$

EXEMPLO: A reta r_1 que passa pelos pontos A_1 (-3,4,2) e B_1 (5,-2,4) , e a reta r_2 que passa pelos pontos  A_2 (-1,2,-3) e B_2 (-5,5,-4) são paralelas. De fato, os vetores diretores destas retas são, respectivamente, $$ \vec{v_1} = \vec{A_1 B_1} = (8,-6,2) \qquad \text{e} \qquad \vec{v_2} = \vec{A_2 B_2} = (-4,3,-1).$$ Usando a condição de paralelismo, temos que $$ \frac{8}{-4} = \frac{-6}{3} = \frac{2}{-1} = -2,$$ portanto, as retas são paralelas.

Retas Ortogonais: A Condição de Ortogonalidade Entre Duas Retas

A condição de ortogonalidade das retas r_1 e r_2 é a mesma dos vetores \vec{v_1} = (a_1 , b_1 , c_1 ) e \vec{v_2} = (a_2 , b_2 , c_2 ) , que definem as direções dessas retas, isto é $$ \vec{v_1} \cdot \vec{v_2} = 0 .$$

EXEMPLO: As retas $$ r_1: \left\{ \begin{array}{lll} y  = 3 \\  \\ \frac{x-3}{8} = \frac{z+1}{-6} \end{array} \right. $$ e $$r_2 = \frac{x}{3} = \frac{y+1}{5} = \frac{z-3}{4}.$$ são ortogonais. De fato, os vetores $$ \vec{v_1} = (8,0,-6) \qquad \text{e} \qquad \vec{v_2} = (3,5,4),$$ respectivamente, são os diretores desta reta, e $$ \vec{v_1} \cdot \vec{v_2} = 8 \times 3 + 0 \times 5 + (-6) \times 4 = 24 – 24 = 0.$$ Portanto, pela consição de ortogonalidade as duas retas são ortogonais.

OBSERVAÇÃO: Uma reta r , cujo vetor diretor \vec{v} é ortogonal (ou normal) a um plano \pi , é ortogonal a qualquer reta contida neste plano. Assim, existem infinitas retas que passam por um ponto A \in \pi e são ortogonais à reta r .

Retas Coplanares: A Condição de Coplanaridade entre Duas Retas

A reta r_1 , que passa por um ponto A_1 (x_1 , y_1 , z_1 ) e tem a direçao de um vetor \vec{v_1} = (a_1 , b_1 , c_1 ) e a reta r_2 , que passa por um ponto A_2 (x_2 , y_2 , z_2 )   e tem a direção de um vetor \vec{v_2} = (a_2 , b_2 , c_2 ) , são coplanares se os vetores \vec{v_1} , \vec{v_2} e \vec{A_1 A_2} forem coplanares, ou seja, se for nulo o produto misto $$ (\vec{v_1} , \vec{v_2} , \vec{A_1 A_2}) = \left| \begin{array}{ccc} a_1 & b_1 & c_1 \\ a_2 & b_2 &  c_2 \\ x_2 – x_1& y_2 – y_1 & z_2 – z_1 \end{array} \right| = 0.$$

EXEMPLO: As retas $$r_1 : \frac{x-2}{2} = \frac{y}{3}= \frac{z-5}{4} \qquad \text{e} \qquad r_2 : -x-5 = y+3= \frac{z-6}{3}$$ são coplanares. De fato, cada uma destas retas tem como respectivos pontos e vetores diretores: $$ A_1 = (2,0,5) \qquad \vec{v_1} = (2,3,4) \\ A_2 = (-5,-3,6) \qquad \vec{v_2} = (-1,1,3).$$ A condição de coplanaridade das retas r_1 e r_2 é satisfeita, pois o produto misto $$ (\vec{v_1} , \vec{v_2} , \vec{A_1 A_2} = \left| \begin{array}{ccc} 2 & 3 & 4 \\ -1 & 1 &  3 \\ -7 & -3 & 1 \end{array} \right| = 0$$ garante este fato.

O ângulo de duas retas

Sejam as retas r_1 , que passa pelo ponto A_1 (x_1 , y_1 , z_1) e tem a direção de um vetor não nulo \vec{v_1} , e r_2 , que passa pelo ponto A_2 (x_2 , y_2 , z_2) e tem a direção de um vetor não nulo \vec{v_2} como a figura abaixo.

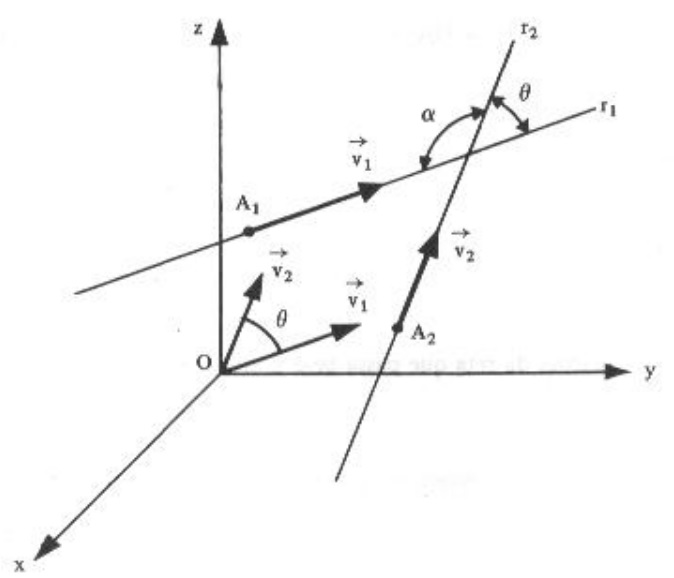
Chama-se de ângulo de duas retas r_1 e r_2 o menor ângulo de um vetor diretor de r_1 e de um vetor diretor de r_2 . Logo, sendo \theta este ângulo, tem-se $$ \text{cos} ( \theta ) = \frac{|\vec{v_1} \cdot \vec{v_2} | }{ | \vec{v_1} | |\vec{v_2}|}, \qquad \text{com } 0 \leq \theta \leq \frac{\pi}{2}.$$

OBSERVAÇÃO: Na figura acima, o ângulo \alpha é o suplementar de \theta e, portanto, \text{cos} ( \alpha ) = - \text{cos} ( \theta )  . O ângulo \alpha é o ângulo formado por - \vec{v_1} e \vec{v_2} ou \vec{v_1} e - \vec{v_2} .

EXEMPLO: Calcular o ângulo entre as retas $$ r: \left\{ \begin{array}{rcl} x  & = & 3 + t \\ & \\ y &= & y = t\\  & \\ z &= & -1-2t \end{array} \right. ; \qquad t \in \mathbb{R} $$ e $$ \frac{x +2 }{ -2 } = y – 3 =z.$$ Os vetores diretores de cada uma destas retas, podem ser dados, respectivamente, por $$ \vec{u} = (1,1,2) \qquad \text{e} \qquad \vec{v} = (-2,1,1)$$ e, assim, pela fórmula do ângulo entre vetores temos que $$ \text{cos} ( \theta ) = \frac{|(1,1,2) \cdot (-2,1,1) | }{ |(1,1,2) | |(-2,1,1)|} = \frac{| -2 +1 -2 |}{\sqrt{1+1+4} \sqrt{4+1+1} } = \\ = \frac{|-3|}{\sqrt{6} \sqrt{6}} = \frac{3}{6} = \frac{1}{2}.$$ Logo, $$ \theta = \text{arc cos} \left( \frac{1}{2} \right) = \frac{ \pi }{3} \text{rad} .$$

A Posição Relativa Entre Duas Retas no Espaço Trimensional

No âmbito da geometria espacial, esta investigação matemática visa abordar a problemática da posição relativa entre duas retas no espaço tridimensional. O presente artigo empreende uma análise meticulosa das configurações geométricas que emergem a partir da interação destas entidades matemáticas, transcendo, assim, os limites da abordagem convencional.

Por meio de uma exploração aprofundada, examinaremos os conceitos fundamentais subjacentes e as complexidades inerentes à relação espacial entre as retas em questão. Antevemos que este estudo proporcionará uma compreensão mais profunda das nuances envolvidas na interseção e paralelismo entre retas no espaço tridimensional, contribuindo, assim, para o corpus do conhecimento matemático.

Considere a reta r_1 , que passa por um ponto A_1 (x_1 , y_1 , z_1 ) e tem a direçao de um vetor \vec{v_1} = (a_1 , b_1 , c_1 ) e a reta r_2 , que passa por um ponto A_2 (x_2 , y_2 , z_2 )   e tem a direção de um vetor \vec{v_2} = (a_2 , b_2 , c_2 ) .

Duas retas r_1 e r_2 podem ser:

1) Coplanares: retas situadas no mesmo plano. Neste caso, as retas podem ser:

a) Concorrentes: r_1 \cap r_2 = \{ I \} (onde I é o ponto de interseção das duas retas r_1 e r_2 ); se (\vec{v_1} , \vec{v_2} , \vec{A_1 A_2}) = 0 e as duas retas não são paralelas, então elas obrigatoriamente concorrentes. O ponto de interseção será dado pela solução do sistema linear que reune as duas equações das retas.

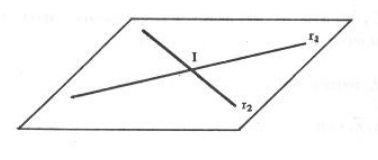
b) Paralelas: r_1 \cap r_2  = \{ \emptyset \} (onde \emptyset é o conjunto vazio); duas retas paralelas sempre serão coplanares, isto é, (\vec{v_1} , \vec{v_2} , \vec{A_1 A_2}) = 0 .

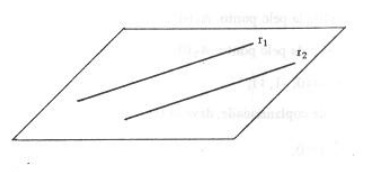
2) Retas Reversas: são duas retas não situadas no mesmo plano e que não contenham nenhum ponto em comum. Para serem reversas, as retas não podem ser coplanares, ou seja, se (\vec{v_1} , \vec{v_2} , \vec{A_1 A_2}) \neq 0 .

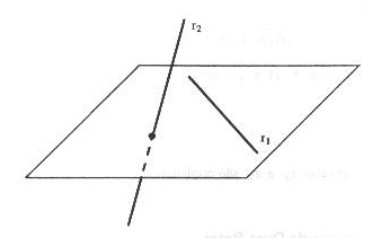
EXEMPLO: Vamos estudar a posição relativa das retas: $$ r_1: \left\{ \begin{array}{rcl} y  & = & 2x-3 \\ & \\ z & = & -x \end{array} \right. $$ e $$r_2 : \left\{ \begin{array}{rcl}x  & = & 1-3t \\ y & = & 4-6t \\ z & = &3t\end{array} \right. .$$ Os vetores diretores neste caso são, respectivamente, $$ \vec{v_1} = (1,2,-1) \qquad  \vec{v_2} = (-3,-6,3)$$ e facilmente vemos que estes vetores são paralelos e não coincidentes (basta ver que o ponto A_1 (0,-3,0) pertence a r_1 , mas não a r_2 ).

EXEMPLO: Vamos estudar a posição relativa das retas: $$ r_1: \frac{x-2}{2} = \frac{y}{3} = \frac{z-5}{4} $$ e $$r_2 : \left\{ \begin{array}{rcl}x  & = & 5+t \\ y & = & 2-t \\ z & = & 7-2t\end{array} \right. .$$ Observe que os vetores diretores de r_1 e r_2 são, respectivamente, $$ \vec{v_1} = (2,3,4) \qquad  \vec{v_2} = (1,-1-2).$$ Podemos perceber que estes vetores não são paralelos pois eles não satisfazem a condição de paralelismo $$ \frac{2}{1} \neq \frac{3}{-1} \neq \frac{4}{-2} .$$ Agora, temos que calcular o produto misto (\vec{v_1} , \vec{v_2} , \vec{A_1 A_2}) para estabelecer a posição realtiva entre as duas retas. Como A_1 (2,0,5 ) e A_2 (5,2,7) são, respectivamente, os pontos por onde passam r_1 e r_2 , então \vec{A_1 A_2} = (3,2,2) . Desta forma, $$ (\vec{v_1} , \vec{v_2} , \vec{A_1 A_2} )= \left| \begin{array}{ccc} 2 & 3 & 4 \\ 1 & -1 &  -2 \\ 3 & 2 & 2 \end{array} \right| = 0,$$ portanto, estas duas retas são coplanares e concorrentes. Agora, para encontrar o ponto de interseção entre estas duas retas precisamos, vamos escrever ambas em suas formas reduzidas e resolver o sistema linear $$ \left\{ \begin{array}{l} x= -y+7 \\ z = 2y+3 \\3x = 2y+6\\ 3z = 4y+15\end{array} \right. .$$ O que nos leva à solução $$ x = 4; \qquad y = 3 ; z= 9 .$$ Portanto o ponto de interseção entre as duas retas será I = (4,3,9). .

EXEMPLO: Vamos estudar a posição relativa entre as retas $$ r_1: \left\{ \begin{array}{rcl}y  & = & 3\\ z & = & 2x\end{array} \right. $$ e $$ r_2 = x=y=z .$$ Observe que neste caso temos que:

• r_1 passa pelo ponto A_1 = (0,3,0) e tem a direção do vetor \vec{v_1} = (1,0,2));
• r_2 passa pelo ponto A_2 = (0,0,0) e tem a direção do vetor \vec{v_2} = (1,1,1));

Com isso, podemos ver que as retas não não paralelas e como $$ (\vec{v_1} , \vec{v_2} , \vec{A_1 A_2} = \left| \begin{array}{ccc} 1 & 0 & 2 \\ 1 & 1 & 1 \\ 0 & -3 & 0 \end{array} \right| \neq 0,$$ podemos afirmar que as retas são reversas.

Reta Ortogonal a Outras Duas

Considere a reta r_1 , que passa por um ponto A_1 (x_1 , y_1 , z_1 ) e tem a direçao de um vetor \vec{v_1} = (a_1 , b_1 , c_1 ) e a reta r_2 , que passa por um ponto A_2 (x_2 , y_2 , z_2 )   e tem a direção de um vetor \vec{v_2} = (a_2 , b_2 , c_2 ) , não sendo paralelas. Qualquer reta r simultaneamente ortogonal às retas r_1 e r_2 terá um vetor diretor paralelo ou igual ao vetor \vec{v_1} \wedge \vec{v_2} .

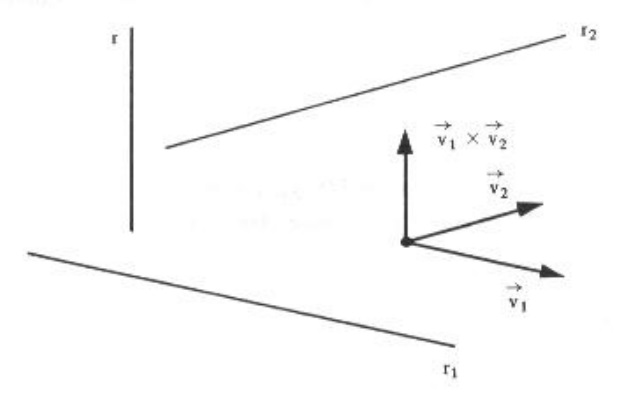
EXEMPLO: Considerando as retas $$ r_1: \left\{ \begin{array}{rcl}x  & = & 2-t\\ y & = & 1 +2t \\ z & = & -3t\end{array} \right. $$ e $$ r_2 = \frac{-x+1}{3} = -z ; y+2 ,$$ teremos como vetores diretores $$ \vec{v_1} = (-1,2,-3) \qquad \text{e} \qquad \vec{v_2} = (-3,0,-1).$$ Então a reta r que é simultaneamente ortogonal a r_1 e r_2 tem como vetor diretor $$ \vec{w} = \vec{v_1} \wedge \vec{v_2} = (-2,8,6) .$$ Portanto a reta que é ortogonal a r_1 e r_2 e passa por um ponto A(-2,1,3) tem equação simétrica dada por $$ \frac{x+2}{-2} = \frac{y-1}{8} =\frac{z-3}{6}.$$

Conclusão

Neste intrigante mergulho na geometria das retas, descobrimos que cada posição relativa revela um universo único de propriedades. Das paralelas à fusão coincidente, passando pelas reversas, as retas nos surpreendem com sua complexidade. Este conhecimento não apenas enriquece nossa compreensão geométrica, mas também destaca a beleza nas interações aparentemente simples.

Leia Mais:

• As Equações da Reta no Espaço R³ – Geometria Analítica
• Vetores no R³: O Produto Misto e Duplo Produto Vetorial
• Vetores no R³: O Produto Vetorial e suas Interpretações Geométricas
• Vetores no R³: O Produto Escalar e suas Interpretações Geométricas