Distâncias entre Pontos, Retas e Planos – Geometria Analítica no Espaço

Explore as maravilhas da geometria tridimensional enquanto revelamos os segredos das distâncias entre pontos, retas e planos. Este artigo desvenda a complexidade do espaço tridimensional, proporcionando insights matemáticos e práticos. Prepare-se para uma jornada fascinante pelo mundo da geometria 3D!

A geometria tridimensional é um universo intrigante que revela suas peculiaridades ao explorarmos as distâncias entre pontos, retas e planos. Neste artigo, mergulharemos nas fórmulas e conceitos essenciais que definem essas distâncias, desvendando a beleza matemática por trás do espaço tridimensional. Desde a distância entre dois pontos até a complexidade das relações entre retas e planos, nossa jornada proporcionará uma compreensão profunda e prática dessa faceta da matemática. Prepare-se para absorver conhecimentos que vão além das fórmulas, permitindo que você visualize e aplique esses conceitos em situações do mundo real.

1 – Distância entre Dois Pontos

A distância d entre dois pontos P_1 (x_1, y_1, z_1) e P_2 (x_2, y_2, z_2) é a norma do vetor \vec{P_1 P_2} , isto é: $$d(P_1 , P2 ) = | \vec{P_1 P_2} | = \sqrt{ (x_2 – x_1 )^2 + (y_2 – y_1 )^2 + (z_2 – z_1 )^2}.$$ Por exemplo, a distância entre os pontos P_1 (7,3,4) e P_2 (1,0,6) é dada por $$d(P_1 , P2 ) = | \vec{P_1 P_2} | = \sqrt{ (1-7 )^2 + (0-3)^2 + (6-4 )^2} = \\ = \sqrt{36+9+4} = \sqrt{49} = 7 u.c. \text{(unidades de comprimento)}$$

1.1 – Exemplo (O Plano Mediador de um Segmento)

Vamos provar que lugar geométrico dos pontos do espaço \mathbb{R} ^3 que equidistam de dois pontos, P_1 (x_1, y_1, z_1) e P_2 (x_2, y_2, z_2) , é um plano perpendicular aos segmento P_1  P_2  que passa pelo seu ponto médio. Chamemos este lugar geométrico de \pi . Desta forma, X(x,y,z) é um ponto de \pi , se, e somente se, d(X,A) = d(X,B). Daí $$ X \in \pi \Leftrightarrow (x – x_1 )^2 + (y – y_1 )^2 + (z – z_1 )^2 = (x – x_2)^2 + (y – y_2 )^2 + (z – z_2 )^2 $$ ou seja, $$ X \in \pi \Leftrightarrow x^2 -2 x_1 x + x_1^2+y^2-2y_1 y +z^2 -2z_1 z + z_1^2 = \\ =  x^2 -2 x_2 x + x_2^2+y^2-2y_2 y +z^2 -2z_2 z + z_2^2$$ $$ X \in \pi \Leftrightarrow 2(x_2 – x_1)x+2(y_2 -y_1)y+2(z_2-z_1)z + x_1^2  + y_1^2 + z_1^2 – x_2^2 – y_2^2 -z_2^2 = 0$$ Logo, uma equação de \pi é dada por $$ \pi : (x_2 – x_1)x+2(y_2 -y_1)y+2(z_2-z_1)z + \frac{1}{2} ( x_1^2  + y_1^2 + z_1^2 – x_2^2 – y_2^2 -z_2^2)=0$$ Ora, sendo os pontos P_1 (x_1, y_1, z_1) e P_2 (x_2, y_2, z_2) distintos, pelo menos uma das três diferenças dos coeficientes desta equação é não-nula,  portanto trata-se da equação geral de um plano. Além disso, vemos também que o vetor $$ \vec{n} = (x_2 – x_1, y_2 -y_1, z_2-z_1)$$ é normal ao plano \pi . Como \vec{n} = \vec{AB} , concluímos que o plano é perpendicular ao segmento AB . Resta ainda provar que o plano \pi passa pelo médio de AB . Seja então $$ M = \left( \frac{x_1 + x_2}{2} , \frac{y_1 + y_2}{2} , \frac{z_1 + z_2}{2} \right)$$ o ponto médio. Substituindo suas coordenadas no primeiro membro da equação de \pi , obtemos $$ \frac{1}{2} (x_2 – x_1 )(x_1 + x_2 ) + \frac{1}{2} (y_2 – y_1 )(y_1 + y_2 )  + \frac{1}{2} (z_2 – z_1 )(z_1 + z_2 ) + \frac{1}{2} ( x_1^2  + y_1^2 + z_1^2 – x_2^2 – y_2^2 -z_2^2) = \\ =  \frac{1}{2} \left[ x_2^2 – x_1^2 + y_2^2 – y_1^2+z_2^2 – z_1^2+x_1^2  + y_1^2 + z_1^2 – x_2^2 – y_2^2 -z_2^2 \right] = 0$$ o que prova que M \in \pi .

2 – Distância de um Ponto a uma Reta

Seja uma reta r definida por um ponto P_1 (x_1, y_1, z_1) e pelo vetor \vec{v} = (a,b,c) e seja P_0 (x_0, y_0, z_0) um ponto qualquer do espaço. Os vetores \vec{v} e \vec{P_1 P_0} determinam um paralelogramos cuja altura corresponde à distância d de P_0 a r que pretendemos calcular como vemos na figura abaixo.

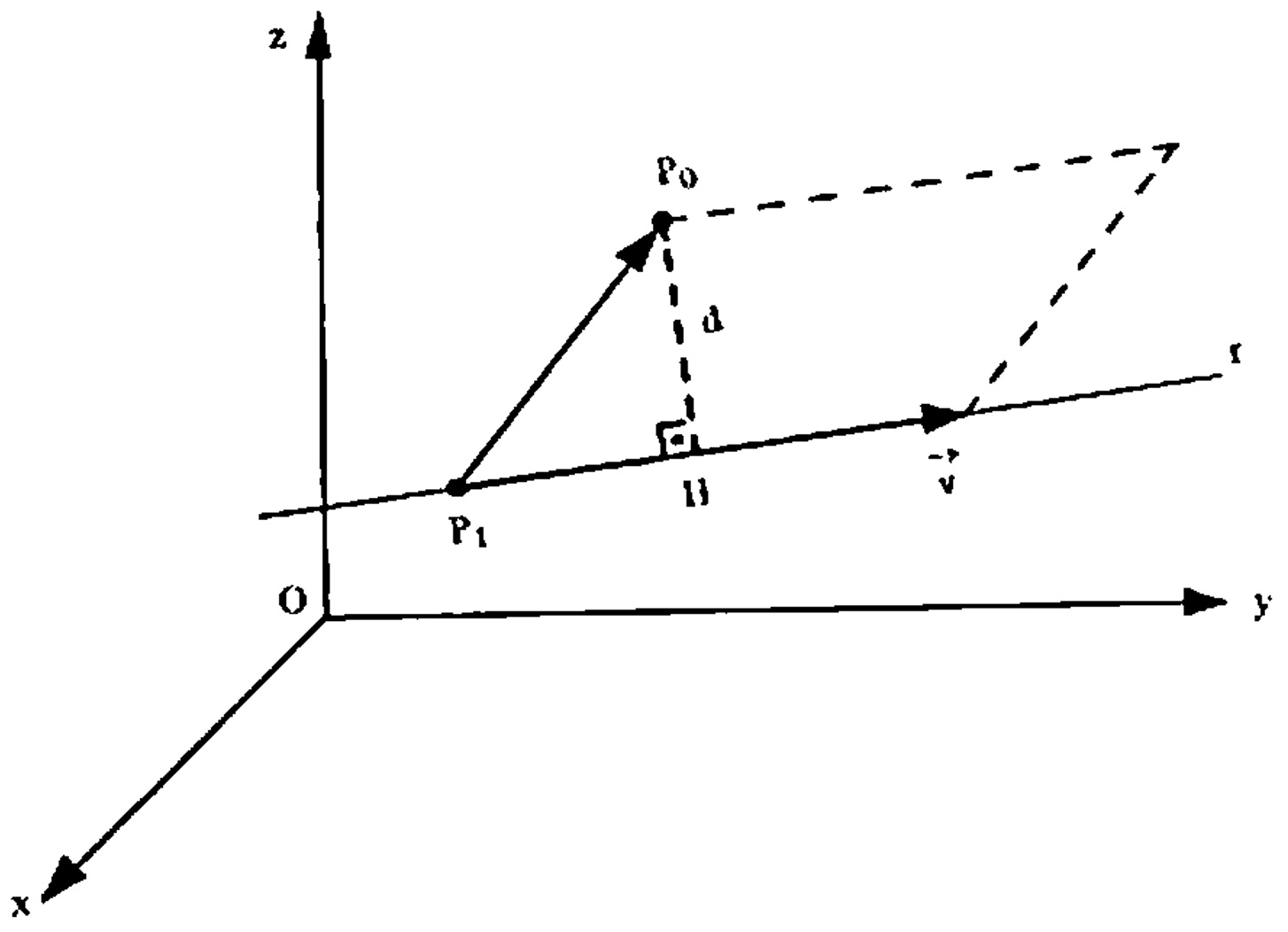
Sabe-se que a área do paralelogramo é dada pelo poduto da base pela altura, ou seja: $$ A = | \vec{v} | d$$ ou, de acordo com a interpretação geométrica do módulo do produto vetorial, por: $$ A = | \vec{v} \wedge \vec{P_1 P_0}|. $$ Portanto, $$ | \vec{v} | d = | \vec{v} \wedge \vec{P_1 P_0}|$$ e, assim, $$ d = \frac{| \vec{v} \wedge \vec{P_1 P_0}|}{| \vec{v} |}.$$ Portanto, $$d(P_0 , r ) = \frac{| \vec{v} \wedge \vec{P_1 P_0}|}{| \vec{v} |} .$$

EXEMPLO: Vamos calcular a distância entre o ponto P_0 (2,0,7) à reta $$r: \frac{x}{2} = \frac{y-2}{2}= z+3.$$ A reta que passa por P_1 (0,2,-3) e tem a direção do vetor \vec{v} = (2,2,1) . Seja ainda o vetor \vec{P_1 P_0} = P_0 - P_1 = (2,-2,10) . Assim, usamos a fórmula que deduzimos anteriormente temos que $$d(P_0 , r ) = \frac{| \vec{v} \wedge \vec{P_1 P_0}|}{| \vec{v} |} = \frac{| (2,2,1)  \wedge (2,-2,10) |}{| (2,2,1) |} = \\ = \frac{| (22,-18,-8) |}{| (2,2,1) |} = \frac{\sqrt{872}}{3} \text{ u. c.} $$

3 – Distância entre duas Retas

A distância entre duas retas r e s é dada pela menor distância entre um ponto de r e um ponto de s .

3.1 – Distância entre duas retas concorrentes

Obviamente, se duas retas r e s são concorrentes, então, por definição, a distância entre estas duas retas será nula.

3.2 – Distância entre duas retas paralelas

Dadas duas retas r e s paralelas, então, a distância entre estas duas retas será será dada pela distância de qualquer ponto P_0 de r à reta s , como podemos ver na figura abaixo.

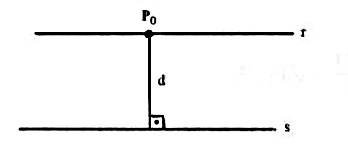
Daí, $$ d(r,s) = d(P_0 , s), \text{ se } P_0 \in r$$ ou $$ d(r,s) = d(P_0 , r), \text{ se } P_0 \in s .$$

EXEMPLO: Vamos calcular a distância entre as retas $$ r: \left\{ \begin{array}{l} y = -2x +3 \\ z = 2x \end{array} \right. \qquad \text{ e } \qquad s: \left\{ \begin{array}{l}x = -1-2t \\ y = 1+4t \\ z = -3-4t \end{array} \right. $$ As retas r e s , são claramente paralelas pois vetores diretores são, respectivamente, \vec{u} = (1,-2,2) e \vec{v} = (-2, 4, -4) , donde podemos verificar que \vec{v} = -2 \vec{u} . Escolhendo o ponto $$ P_0 (0,3,0) \in r $$ e sabendo que $$P_1 (-1,1,-3) \in s$$ temos que  $$d(P_0 , s ) = \frac{| \vec{v} \wedge \vec{P_1 P_0}|}{| \vec{v} |} = \frac{| (-2, 4, -4) \wedge (1,2,3) |}{| (-2, 4, -4) |} = \sqrt{13} \text{ u. c.} $$

3.3 – Distância entre duas retas reversas

Consideremos duas retas r e s reversas: a reta r definida por um ponto P_1 (x_1, y_1, z_1) e pelo vetor \vec{u} (a_1, b_1, c_1) e a reta s definida por um ponto P_2 (x_2, y_2, z_2) e pelo vetor \vec{v} (a_2, b_2, c_2) . Nestas condições, sabemos que os vetores \vec{u} , \vec{v} e \vec{P_1 P_2} = (x_2 - x_1, y_2 - y_1, z_2 -z_1) determinam um paralelepípedo como vemos na figura abaixo.

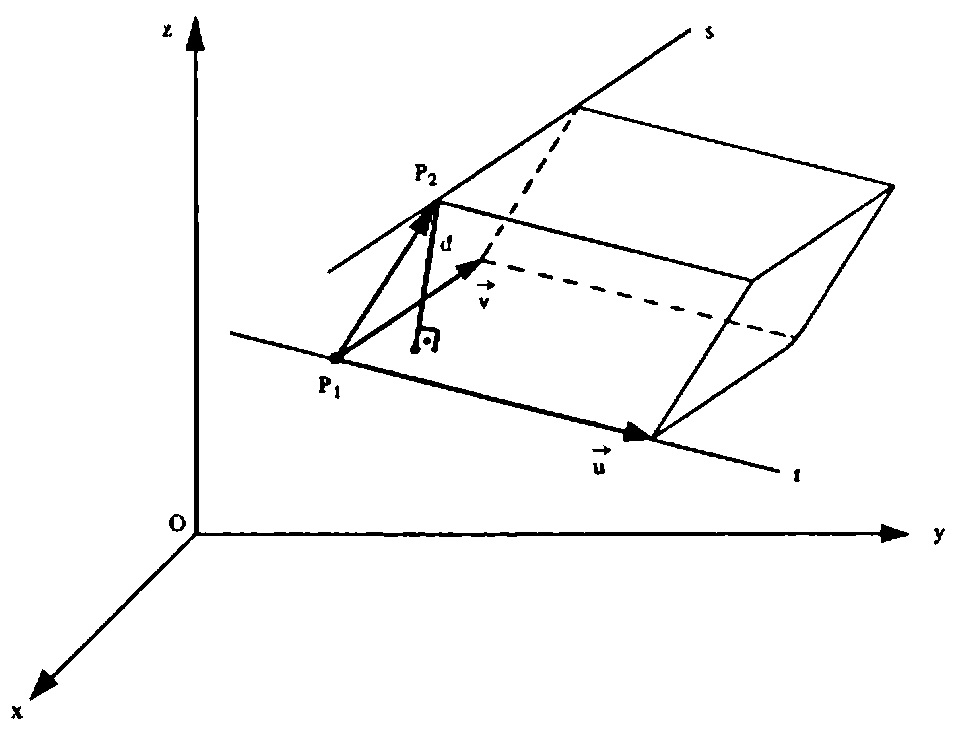
A base deste paralelepípedo é definida pelos vetores \vec{u} e \vec{v} e sua altura corresponde à distância d entre as retas r e s porque a reta s   é paralela ao plano da base do paralelepípedo uma vez que sua direção é a do vetor \vec{v} .Sabe-se que o volume V de um paralelepípedo é dado pelo produto da área da base pela altura $$ V = | \vec{u} \wedge \vec{v} | d$$ ou, de acordo com a interpretação geométrica do módulo do produto misto, por: $$ V = | (\vec{u}, \vec{v}, \vec{P_1 P_2})|$$ Daí, comparando as duas fórmulas do volume, encontramos $$ | \vec{u} \wedge \vec{v} | d = | (\vec{u}, \vec{v}, \vec{P_1 P_2})| $$ o que nos leva a $$d = \frac{ | (\vec{u}, \vec{v}, \vec{P_1 P_2})|}{| \vec{u} \wedge \vec{v} |}.$$ Portanto, $$d(r,s)_{reversas} = \frac{ | (\vec{u}, \vec{v}, \vec{P_1 P_2})|}{| \vec{u} \wedge \vec{v} |}.$$

EXEMPLO: Vamos calcular a distância entre as retas $$ r: \left\{ \begin{array}{l} y = 1 \\ x+2 = \frac{z-4}{-2} \end{array} \right. \qquad \text{ e } \qquad s: \left\{ \begin{array}{l}x = 3 \\ y = 2t-1 \\ z = -t +3 \end{array} \right. $$ A reta r passa pelo ponto P_1 (-2,1,4) e tem a direção do vetor \vec{u} = (1,0,-2) e a reta s passa pelo ponto P_1 (3,-1,3) e tem a direção do vetor \vec{v} = (0,2,-1) . Então, \vec{P_1 P_2} = (5,-2,-1) , $$ (\vec{u}, \vec{v}, \vec{P_1 P_2}) = \left| \begin{array}{ccc} 1 & 0 & -2 \\ 0 & 2 & -1 \\ 5 & -2 & 12 \end{array}  \right| = 16$$ e $$ \vec{u} \wedge \vec{v} = \left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ 1 & 0 & -2 \\ 0 & 2 & -1 \end{array} \right| = (4,1,2).$$ Pelo produto misto vemos que as retas são reversas, pois os três vetores não são coplanares, logo, a distância entre elas será dada por $$d(r,s)_{reversas} = \frac{ | (\vec{u}, \vec{v}, \vec{P_1 P_2})|}{| \vec{u} \wedge \vec{v} |} = \frac{16}{\sqrt{16+1+4}}= \frac{16}{\sqrt{21}}.$$

Distância de um Ponto a um Plano

Seja um ponto P_0 (x_0 , y_0 , z_0 ) e um plano $$ \pi : ax+by+cz+d = 0 .$$ Sejam A o pé da perpendicular conduzida por P_0 sobre o plano \pi e P (x , y , z ) um ponto qualquer deste plano conforme a figura abaixo.

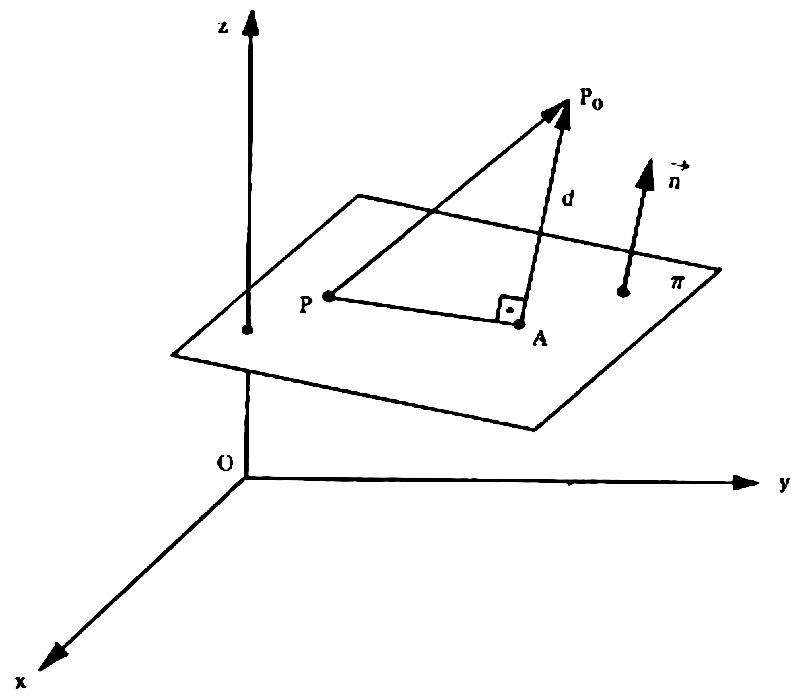
O vetor \vec{n} = (a,b,c) é normal ao plano \pi e, portanto, o vetor \vec{AP_0} tem a mesma direção de \vec{n} . A distância d do ponto P_0 ao plano \pi é:$$ d(P_0, \pi ) = | \vec{AP_0} |.$$ Observando que o vetor \vec{AP_0} é a projeção do vetor \vec{PP_0} na direção de \vec{n} , assim, $$ d(P_0, \pi ) = | \vec{AP_0} | = \left| \vec{PP_0} \cdot \frac{\vec{n}}{| \vec{n} |}  \right|,$$ mas: $$ \vec{PP_0} = (x_0 – x , y_0 -y , z_0 – z ) $$ e $$ \frac{\vec{n}}{| \vec{n} |} = \frac{(a,b,c)}{\sqrt{a^2 + b^2 +c^2}}.$$ Logo $$ d(P_0, \pi ) =  \left| (x_0 – x , y_0 -y , z_0 – z ) \cdot \frac{(a,b,c)}{\sqrt{a^2 + b^2 +c^2}} \right| \\ d(P_0, \pi ) =  \left|  \frac{a(x_0 – x) + b(y_0 -y) + c (z_0 -z)}{\sqrt{a^2 + b^2 +c^2}} \right| \\ d(P_0, \pi ) =  \frac{ | ax_0 + by_0 + c z_0 – ax -by -cz|}{\sqrt{a^2 + b^2 +c^2} } .$$ Como P é um ponto do plano \pi , então $$-ax-by-cz = d $$ e, portanto, $$ d(P_0, \pi ) =  \frac{ | ax_0 + by_0 + c z_0 +d|}{\sqrt{a^2 + b^2 +c^2} }.$$

EXEMPLO: Vamos calcular a distância entre o ponto P_0 (-4,2,5) ao plano \pi: 2x+y+2z+8 = 0 . Observando que as componentes do vetor normal ao plano \pi é dado por \vec{n} = (2,1,2) , então, pela fórmula acima encontramos que $$ d(P_0, \pi ) =  \frac{ | ax_0 + by_0 + c z_0 +d|}{\sqrt{a^2 + b^2 +c^2} } = \frac{ | 2(-4)+1(2)+2(5)+8|}{\sqrt{2^2 +1^2 +2^2} } = \frac{12}{3} = 4 \text{ u. c.}$$

Distância entre Dois Planos

A distância entre dois planos é definida somente quando o planos forem paralelos. Dados dois planos \pi _1 e \pi _2 , paralelos, a distância d entre eles é a distância de um ponto qualquer de um dos planos ao outro plano. Daí, $$ d(\pi _1 , \pi_2 ) = d(P_0 , \pi_2 ), \text{ se } P_0 \in \pi _1$$ ou $$d(\pi _1 , \pi_2 ) = d(P_0 , \pi_1 ), \text{ se } P_0 \in \pi _2 .$$ Portanto, $$ d(\pi _1 , \pi_2 ) = d(P_0, \pi_2 ) =  \frac{ | a_2 x_0 + b_2 y_0 + c_2 z_0 +d_2 |}{\sqrt{a^2 + b^2 +c^2} }.$$

Um caso particular se dá quando os vetores normais a cada um dos planos são iguais: $$ \pi _1 : a_1 x +b_1 y +c_1 z +d_1 =0 \qquad \text{e} \qquad  \pi _2 : a_2 x +b_2 y +c_2 z +d_2 =0 .$$ Neste caso, a fórmula se reduziria a $$ d(\pi _1 , \pi_2 ) = \frac{ | d_1 – d_2|}{\sqrt{a^2 + b^2 +c^2} }.$$

EXEMPLO: Vamos calcular a distância entre os planos $$ \pi _1 :2x-2y+z-5 = 0 \qquad \text{e} \qquad \pi _2 : 4x-4y+2z+14 = 0 $$ Uma primeira forma de resolver este problema é usar o fato de que P_0 (0,0,5) é um ponto de \pi _1 e \vec{n} = (4,-4,2) é o vetor normal a \pi _2 . Portanto, de acordo com a fórmula descrita anteriormente $$ d(\pi _1 , \pi_2 ) = d(P_0, \pi_2 ) =  \frac{ | 4(0) – 4(0)+2(5) +14 |}{\sqrt{4^2 + (-4)^2 +2^2} }=\frac{10 + 14 }{\sqrt{36}} = \frac{24}{6}= \frac{12}{3} = 4 \text{ u. c.}$$ Ainda podemos resolver este mesmo problema dividindo a equação de \pi _2 por 2: $$ \pi _1 :2x-2y+z-5 = 0 $$ $$ \pi _2 : 4x-4y+2z+14 = 0 \Leftrightarrow \pi _2 : 2x-xy+z +7 = 0 $$ e, daí, como os planos possuem o mesmo vetor normal, calcular a distância entre os planos da seguinte maneira $$ d(\pi _1 , \pi_2 ) = \frac{ | 5 – 7 |}{\sqrt{2^2 + (-2)^2 +1^2} } = \frac{12}{3} = 4 \text{ u. c.}$$

Distância entre Retas e Planos

A distância de uma reta a um plano é definida somente quando a reta é paralela ao plano. Dada uma reta r paralela a um plano \pi , a distância d da reta ao plano é a distância de um ponto qualquer da reta ao plano, isto é, $$ d(r, \pi) = d(P_0 , \pi) \text{ com } P_0 \in r$$ que foi definida nas seções anteriores.

Conclusão

Ao final desta exploração fascinante no mundo tridimensional, compreendemos que a geometria vai além de simples fórmulas; ela oferece uma visão única sobre as relações espaciais. Dominar as distâncias entre pontos, retas e planos amplia nosso entendimento matemático e fornece ferramentas essenciais para aplicações práticas. Este mergulho profundo na geometria tridimensional revelou não apenas a beleza intrínseca das fórmulas, mas também sua utilidade tangível em problemas do mundo real. Ao abraçar a complexidade do espaço 3D, fortalecemos nossa capacidade de compreender e resolver desafios matemáticos, ampliando assim nosso horizonte intelectual.

Leia Mais

• Retas e Planos nos Espaço Tridimensional: 9 Exercícios Resolvidos
• Posições Relativas entre Planos e Retas no Espaço Tridimensional R³
• Retas no Espaço Euclidiano R³: Posiçoes Relativas Entre Retas.
• Vetores no R³: O Produto Misto e Duplo Produto Vetorial
• Vetores no R³: O Produto Vetorial e suas Interpretações Geométricas