PRECISANDO DE AJUDA COM SEUS EXERCÍCIOS SOBRE ESTE CONTEÚDO? Entre em contato com a gente via WhatsApp clicando aqui. |
O folium de Descartes é uma curva plana proposta por Descartes para desafiar as técnicas de extremos de Fermat. O nome vem da palavra latina folium, que significa “folha” e na forma paramétrica, esta curva é parametrizada por $$\vec{r}(t)= \frac{3at}{1 + t^3} \vec{i} + \frac{3at^2}{1 + t^3} \vec{j} .$$
Esse fólio foi discutido pela primeira vez por Descartes em 1638, mas, embora ele tenha encontrado a forma correta da curva no quadrante positivo, ele acreditava que essa forma de folha se repetia em cada quadrante como as quatro pétalas de uma flor.
O fólio de Descartes está relacionado à trissetriz de Maclaurin, curva que começou a ser estudada por Colin Maclaurin em 1742. Tal como tantas outras, o seu estudo foi abordado no sentido de encontrar uma solução para um dos antigos problemas, neste caso o da trissecação de um ângulo.
Quem Foi Descartes?
René Descartes (1596-1650) foi um matemático e filósofo de primeira ordem, um importante pensador científico e um metafísico original. Durante o curso de sua vida, ele foi primeiro um matemático, depois um cientista natural ou “filósofo natural” e um terceiro metafísico. O criador da geometria analítica, base matemática que mudaria a ciência.
Na matemática, ele desenvolveu as técnicas que tornaram possível a geometria algébrica (ou “analítica”). Na filosofia natural, ele pode ser creditado com várias realizações específicas: co-enquadrador da lei seno de refração, desenvolvedor de uma importante explicação empírica do arco-íris e proponente de uma explicação naturalística da formação da Terra e dos planetas (um precursor à hipótese nebular).
Mais importante ainda, ele ofereceu uma nova visão do mundo natural que continua a moldar nosso pensamento hoje: um mundo de matéria possuindo algumas propriedades fundamentais e interagindo de acordo com algumas leis universais. Esse mundo natural incluía uma mente imaterial que, nos seres humanos, estava diretamente relacionada ao cérebro; dessa forma, Descartes formulou a versão moderna do problema mente-corpo.
Na metafísica, ele forneceu argumentos para a existência de Deus, para mostrar que a essência da matéria é a extensão e que a essência da mente é o pensamento. Descartes afirmou desde o início possuir um método especial, que foi exibido de várias maneiras na matemática, filosofia natural e metafísica, e que, na última parte de sua vida, incluiu, ou foi suplementado por, um método de dúvida.
Descartes era conhecido entre os eruditos em sua época como um matemático de ponta, como o desenvolvedor de uma nova e abrangente física ou teoria da natureza (incluindo os seres vivos) e como o proponente de uma nova metafísica.
O Fólio de Descartes
O Fólio de Descartes é famoso por causa de um incidente no desenvolvimento do cálculo. Descartes desafiou Pierre de Fermat a encontrar a linha tangente à curva em um ponto arbitrário, já que Fermat havia descoberto recentemente um método para encontrar linhas tangentes. Fermat resolveu o problema facilmente, algo que Descartes não foi capaz de fazer.
Uma curva parametrizada \vec{r} (t) é chama de simples se ela não possui pontos de auto-interseção. Ou seja, se existirem pontos t_0 e t_1 , tais que \vec{r} (t_0) = \vec{r} (t_1) , a curva não é simples. O Fólio de Descartes não é uma curva simples, como podemos observar no esboço abaixo:
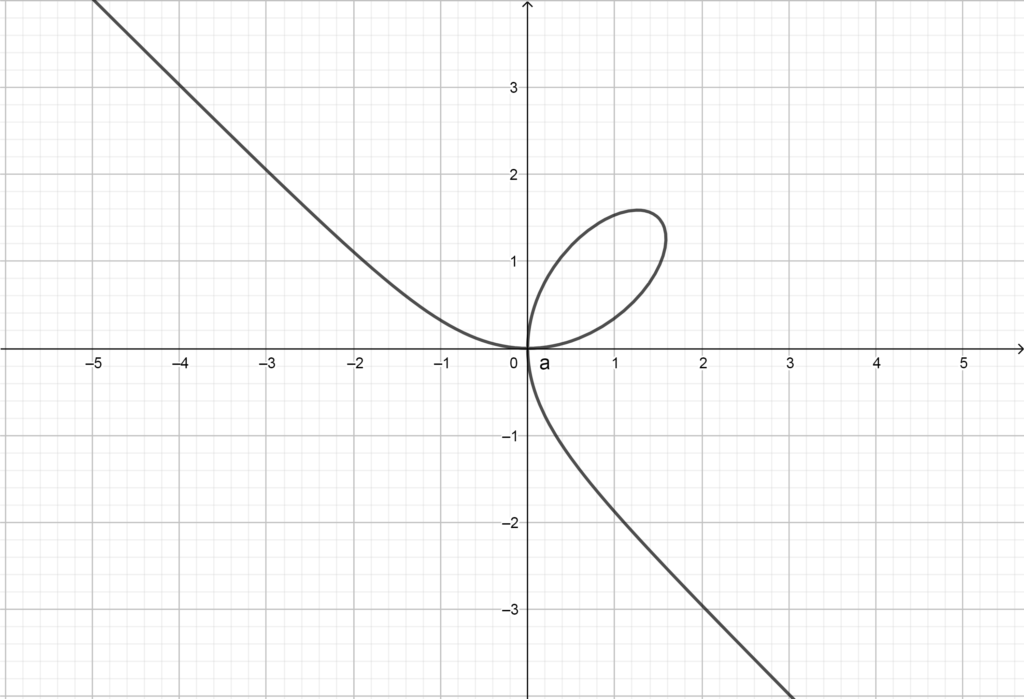
Pela sua parametrização podemos ficar tentados a dizer que esta curva não possui um ponto múltiplo na origem, pois apenas t=0 tem imagem na origem do sistema. Este fenômeno será explicado abaixo.
O fólio tem equação cartesiana dada por x^3 + y^3 = 3axy e uma assíntota de equação dada por x + y + a =0 , mas facilmente podemos mostrar que todos os pontos da curva parametrizada por $$\vec{r}(t)= \frac{3at}{1 + t^3} \vec{i} + \frac{3at^2}{1 + t^3} \vec{j}$$ satisfazem esta equação cartesiana.
De fato, fazendo x = \dfrac{3at}{1 + t^3} e y = \dfrac{3at^2}{1 + t^3} observamos que $$ x^3 + y^3 = \left( \frac{3at}{1 + t^3} \right)^3 + \left( \frac{3at^2}{1 + t^3} \right)^3 = \frac{27a^3 t^3 + 27a^3 t^6}{(1 + t^3)^3} = $$ $$ = \frac{27 a^3 t^3 (1 + t^3)}{(1 + t^3)^3} = \frac{27a^3 t^3}{(1 + t^3)^2} = 3a \left( \frac{3at}{1+t^3} \right) \left( \frac{3at^2}{1+t^3} \right) = 3a xy .$$
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Com esta parametrização podemos observar porque temos a impressão de que o fólio de Descartes não tem um ponto múltiplo na origem. Isso se dá pois podemos mostrar que quando t \rightarrow \pm \infty a curva tenderá novamente à origem.
De fato, $$\lim_{t \rightarrow \infty}{\vec{r}(t)} = \vec{i} \lim_{t \rightarrow \infty}{\frac{3at}{1 + t^3}} + \vec{j} \lim_{t \rightarrow \infty}{\frac{3at^2}{1 + t^3}} = $$ $$ = \vec{i} \lim_{t \rightarrow \infty}{\frac{3at}{t^3}} + \vec{j} \lim_{t \rightarrow \infty}{\frac{3at^2}{t^3}}= \vec{i} \lim_{t \rightarrow \infty}{\frac{3a}{t^2}} + \vec{j} \lim_{t \rightarrow \infty}{\frac{3a}{t}}= (0,0)$$ ou seja, quando o parâmetro tender a \pm \infty o fólio tenderá novamente à origem, e por isso, a continuidade garantirá que a curva possui um ponto múltiplo.
O que acontece é que com t \in ( - \infty , -1) a curva tem um arco que vem na direção da origem ao longo do 4º quadrante, enquanto com t \in ( -1 , + \infty) a curva tem um arco que decresce ao longo do 2º quadrante, corta a origem quanto t = 0 e tende novamente à origem. Obviamente, t = - 1 é um ponto de descontinuidade desta curva. Tentamos ilustrar este comportamento abaixo:
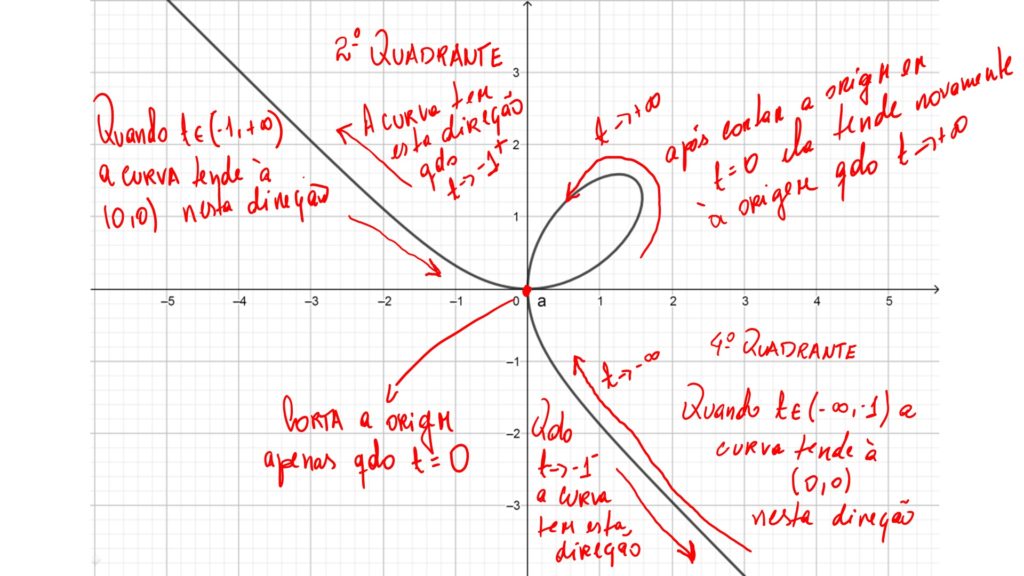
O fólio de Descartes ainda pode ser escrito por coordenadas polares como $$ r = \frac{3a sen( \theta ) cos ( \theta ) }{sen^3 ( \theta ) + cos ^3 ( \theta )}$$ que é equivalente a $$ r = \frac{3a sec( \theta ) tan ( \theta ) }{1 + tan ^3 ( \theta )}.$$