Curvas | Reta Tangente, Curvatura, Torção e Fórmulas de Frenet

Nesse artigo queremos desenvolver os conceitos de parametrização, comprimento de arco e deslocamento de partícula ligados às curvas no espaço.

Uma função de uma variável a valores em \mathbb{R}^n é uma função F:A \rightarrow \mathbb{R}^n, onde A é um subconjunto de \mathbb{R}.

Esta função associa a cada t \in \mathbb{R} um vetor do \mathbb{R}^n.

O conjunto A é o domínio da função F, que consideraremos sempre como um intervalo ou uma união de intervalos, e notado por D_F.

O conjunto $$ImF=\left\{F(t) \in \mathbb{R}^n ; t \in D_F \right\}$$ é a imagem ou a trajetória de F.

Esta função é, por muitas vezes, denominada de função vetorial ou curva.

Curvas no Espaço

Comumente ma função de uma variável a valores no \mathbb{R}^n é denominada curva parametrizada.

Assim, uma função $$f(t)=(x_1(t), x_2(t),…,x_n(t))\;\;\;\;t\in \mathbb{R}$$ é uma curva e as funções reais x_i(t),\; i=1,...,n, são as equações paramétricas da curva e t é chamado de parâmetro.

Porém, com mais acuidade matemática definimos como curva o conjunto de todos os pontos (x(t), y(t), z(t)) do espaço determinados por uma função vetorial de uma variável.

Uma curva plana é uma curva que está contida em plano do espaço. Uma curva que não é plana é chamada de reversa.

Uma curva parametrizada \vec{f} (t) é fechada se \vec{f} (a) = \vec{f} (b) se \vec{f} (t) está definida para t \in [a,b].

Reta Tangente à Curva

Considere uma curva C parametrizada em um parâmetro t qualquer. A reta tangente a C num ponto P = r(t_0) é definida, em sua forma paramétrica por $$p(w) = r(t_0) + w \frac{dr}{dt}(t_0).$$

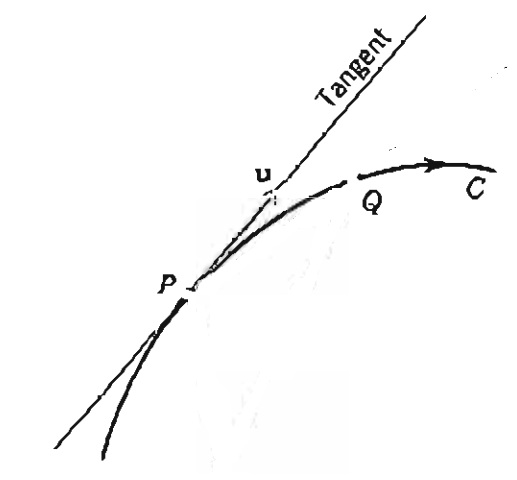
EXEMPLO

No caso do círculo $$r(t) = r\cos{t} \vec{i} + r \sin{t} \vec{j}$$ temos que $$\frac{dr}{dt}(t) = -r\sin{t} \vec{i} + r \cos{t} \vec{j}$$ e a reta tangente ao círculo em um ponto P = r(t_0) tem equação dada por $$q(w) = r\cos{t_0} \vec{i} + r \sin{t_0} \vec{j} + w (-r\sin{t_0} \vec{i} + r \cos{t_0} \vec{j}).$$

Fazendo r=2 e t_0 = \pi/4 ficamos com $$q(w) = r\frac{\sqrt{2}}{2} \vec{i} + r \frac{\sqrt{2}}{2} \vec{j} + w (-r\frac{\sqrt{2}}{2} \vec{i} + r \frac{\sqrt{2}}{2} \vec{j}) = r\left( \frac{\sqrt{2}}{2},r\frac{\sqrt{2}}{2} \right)+ w r \left( -\frac{\sqrt{2}}{2}, r\frac{\sqrt{2}}{2} \right).$$

VETOR TANGENTE UNITÁRIO

Dada uma curva suave C dada por f(t) = (x(t), y(t), z(t)) , o vetor tangente à curva em cada ponto de C é dado por f'(t) = (x'(t), y'(t), z'(t)) .

Logo o vetor tangente unitário à curva C em cada ponto é dado por $$u'(t) = \frac{f'(t)}{|f'(t)|} $$

Se a curva é parametrizada pelo comprimento de arco, então o vetor tangente unitário é o próprio vetor tangente. (Saiba o que é uma curva parametrizada pelo comprimento de arco, nesse artigo).

Além disso, se a curva C é parametrizada pelo comprimento de arco, dada por h(s). Se o vetor tangente unitário u(s) é diferente do vetor nulo, então u'(s) é ortogonal a u(s)e aponta para o lado côncavo de C.

Curvatura

Seja C uma curva suave dada por h(s), 0 \leq s \leq l . Definimos a curvatura de C em um ponto como $$ k(s) = | h”(s)|.$$

Ou seja, a expressão nos diz que a curvatura é a taxa de variação do vetor tangente unitário u(s) em relação ao comprimento de arco s. Como este vetor não varia em intensidade, ela exprime a razão de variação da direção do vetor u(s). Assim, geometricamente, podemos dizer que a curvatura k(s) nos dá a razão de variação da direção da tangente quando  esta se desloca sobre a curva.

TEOREMA:

Se uma curva suave C é dada por f(t), onde t é um parâmetro qualquer, sua curvatura pode ser expressa por $$ k(t) = \frac{|f'(t) \times f” (t)|}{|f’ (t)| ^3} .$$

CÍRCULO DE CURVATURA:

Quando k \neq 0 em um ponto P de uma curva C, podemos encontrar o círculo de curvatura de C em P. Este círculo tem as seguintes características:

• Esta contido no plano formado pelos vetores u e u’.
• Está centrado na semi-reta de origem em P, na direção do vetor u’.
• Tem raio R = \frac{1}{k} , onde k é a curvatura de C em P.

O raio R do círculo de curvatura é chamado de raio de curvatura de C, em P.

Como a curvatura de uma circunferência de raio R é 1/R vemos que a curvatura de C coincide com a de seu círculo de curvatura em P.

Podemos dizer que, nas proximidades de P, o círculo de curvatura é o círculo que melhor aproxima a curva.

EXEMPLO

Calcular a curvatura da circunferência $$ C: f(t) = (R cos(t), R sen(t)), t \in [0, 2 \pi].$$

A parametrização desta curva pelo comprimento de arco é dada por $$h(s) = f(t(s)) = \left( R cos \left(\frac{s}{R} \right), R sen \left(\frac{s}{R} \right) \right) , 0 \leq s \leq 2 \pi R , $$ onde s é o parâmetro comprimento de arco.

Temos então $$ u(s) = h’ (s) = \left(-sen \left(\frac{s}{R} \right), cos \left(\frac{s}{R} \right) \right)$$ e $$u'(s) = \left(-\frac{1}{R} cos \left(\frac{s}{R} \right), -\frac{1}{R} sen \left(\frac{s}{R} \right) \right) .$$

Portanto, a curvatura de C é dada por $$ k(s) = | u’ (s) | = \frac{1}{R} .$$

EXEMPLO

Encontrar a curvatura da parábola r(t) = (t, t^2), - \infty < t < \infty .

Usando a fórmula  $$ k(t) = \frac{|f'(t) \times f” (t)|}{|f’ (t)| ^3}, $$ obtemos $$ k(t) = \frac{|(1, 2t) \times (0,2)|}{|(1,2t)| ^3}  = \frac{2}{(\sqrt{1 + 4t^2}) ^3}$$

Podemos observar, neste resultado, que para t=0, a curvatura tem seu valor máximo e que ela tende a zero quando |t| tende a + \infty .

Vetor Normal Principal

Quando k(s) é diferente de zero, podemos definir um vetor unitário p(s), chamado vetor normal principal como $$ p(s) = \frac{u'(s)}{k(s)} ;$$

O vetor normal principal p(s) é ortogonal ao vetor tangente u(s) e aponta para o lado côncavo de C.

Os vetores u e p como foram definidos, respectivamente, calculados em um ponto P da curva, definem um plano. Este plano contém o círculo de curvatura de C em P, e é chamado Plano Osculador.

Quando a curva é uma curva plana, com exceção da reta, o plano osculador coincide com o plano da curva.

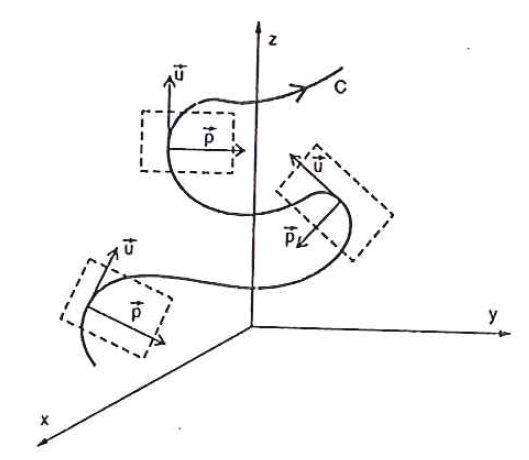
Vetor Binormal

O vetor binormal denotado por b(s), é definido como o vetor unitário, normal ao plano osculador que é dado por $$ b(s) = u(s) \times p(s). $$

Os três vetores, u, p e b determinam um sistema de coordenadas que se move sobre a curva C. O triedro determinado por estes vetores é chamado triedro de Frenet da curva C.

A figura abaixo mostra esse triedro em um ponto P de uma curva C.

EXEMPLO:

O vetor binormal da circunferência $$ C: f(t) = (2 cos(t), 2 sen(t)), t \in [0, 2 \pi]$$ é dado por $$b(s) = u(s) \times p(s)$$ onde u(s) = \left(-sen \left(\frac{s}{2} \right), cos \left(\frac{s}{2} \right) \right) e p(s) = \left(-cos \left(\frac{s}{2} \right), -sen \left(\frac{s}{2} \right) \right) , o que nos leva a $$b(s) = u(s) \times p(s) = \left(-sen \left(\frac{s}{2} \right), cos \left(\frac{s}{2} \right) \right) \times \left(-cos \left(\frac{s}{2} \right), -sen \left(\frac{s}{2} \right) \right) = (0,0,1).$$

EXEMPLO:

Determinar o vetor binormal da hélice circular $$C: f(t) = (acos(t), a sen(t), bt), t \geq 0, a,b> 0.$$ em um qualquer ponto.

Temos que a função comprimento de arco de C é $$ s = \int_{0}^{t}{\sqrt{a^2 + b^2} dt} = \sqrt{a^2 + b^2} t .$$

Portanto, $$ t = \frac{s}{\sqrt{a^2 + b^2}}.$$ Chamando \sqrt{a^2 + b^2} = \omega , temos t = s/ \omega .

Logo, $$h(s) = \left(a cos \left(\frac{s}{\omega} \right), a sen \left(\frac{s}{\omega} \right), b \frac{s}{\omega} \right). $$

O vetor tangente unitário é $$u(s) = h'(s) = \left(- \frac{a}{\omega} sen \left(\frac{s}{\omega} \right), \frac{a}{\omega} cos \left(\frac{s}{\omega} \right), \frac{b}{\omega} \right)$$

A curvatura é $$ k(s) = | u'(s) | = \left|  \left(- \frac{a}{\omega ^2} cos \left(\frac{s}{\omega} \right), – \frac{a}{\omega ^2} sen \left(\frac{s}{\omega} \right),0 \right) \right| = \frac{a}{\omega ^2} .$$

O vetor normal principal é $$p(s) = \frac{u'(s)}{k(s)} = \frac{ \omega ^2}{a} \left(- \frac{a}{\omega ^2} cos \left(\frac{s}{\omega} \right), – \frac{a}{\omega ^2} sen \left(\frac{s}{\omega} \right),0 \right) = \left( – cos \left(\frac{s}{\omega} \right), – sen \left(\frac{s}{\omega} \right),0 \right).$$

Portanto, o vetor binormal é dado por $$b(s) = u(s) \times p(s) = \left(\frac{b}{\omega} sen \left(\frac{s}{\omega} \right), – \frac{b}{\omega} cos \left(\frac{s}{\omega} \right),  \frac{a}{\omega} \right). $$

Torção

A menos de sinal, a torção exprimirá a taxa de variação do vetor binormal.

É possível mostrar que $$b'(s) = \alpha p(s)$$ onde \alpha é um escalar. Se fizermos \alpha = - T obtemos $$b'(s) = – T p(s) $$ e multiplicando p(s) escalarmente, chegamos a $$ T = -b'(s) . p(s) .$$

A função escalar T é chamada de torção da curva C e $$T = \pm | b'(s) |, $$ ou seja, a menos de sinal, a torção é a taxa de variação do vetor binormal.

Fórmulas de Frenet-Serret

As Fórmulas de Frenet permitem caracterizar diversos tipos de curvas pelas propriedades de sua curvatura e torção.

Por exemplo, quando a curvatura é nula, temos uma reta, e quando a torção é nula, temos uma curva plana.

As Fórmulas de Frenet-Serret são dadas por $$u’ = k p$$ $$p’ = -k u + T b$$ $$b’ = – T p.$$

O Teorema Fundamental das curvas mostra que, quando k \neq 0 , a curvatura e a torção descrevem geometricamente a curva, exceto por sua posição no espaço.

Leia Mais:

• Curvas no Espaço | Funções de uma Variável Real a Valores Vetoriais
• Curvas | Limite e Continuidade de uma Função Vetorial
• Curvas | A Derivada de Funções Vetoriais
• EFEITO BORBOLETA | Edward Lorenz e a Teoria do Caos
• GRÁFICOS | Da Análise Estatística ao Mercado de Ações
• Apocalipse | A Ciência do Fim do Mundo
• Universos Paralelos: Ciência ou Ficção Científica?