Entenda Tudo Sobre Números Irracionais: Exemplos e Curiosidades Históricas

Os números irracionais são aqueles que não podem ser escritos como uma fração, como o \pi ou \sqrt{2} , por exemplo. Explore o mundo fascinante dos números irracionais. Aprenda com exemplos claros e descubra histórias intrigantes por trás desses números enigmáticos. Clique agora para desvendar!

Introdução aos Números Irracionais

Assim como existem números decimais que podem ser escritos como frações, com numerador e denominador inteiros (que são chamados de números racionais), há aqueles que não admitem tal representação. São as dízimas não-periódicas. Denotamos o conjunto dos números reais por \mathbb{R}. Temos \mathbb{R} \supe \mathbb{Q} e todo número real que não é racional é dito irracional. 

Ou seja, definimos os números irracionais como os números reais que não são racionais. Vejamos alguns exemplos de números irracionais:

1. O número 0,21211211121111… não é dízima periódica, pois os algarismos após a vírgula não se repetem periodicamente;
2. O número 1,203040… também não comporta representação fracionária, pois não é dízima periódica;
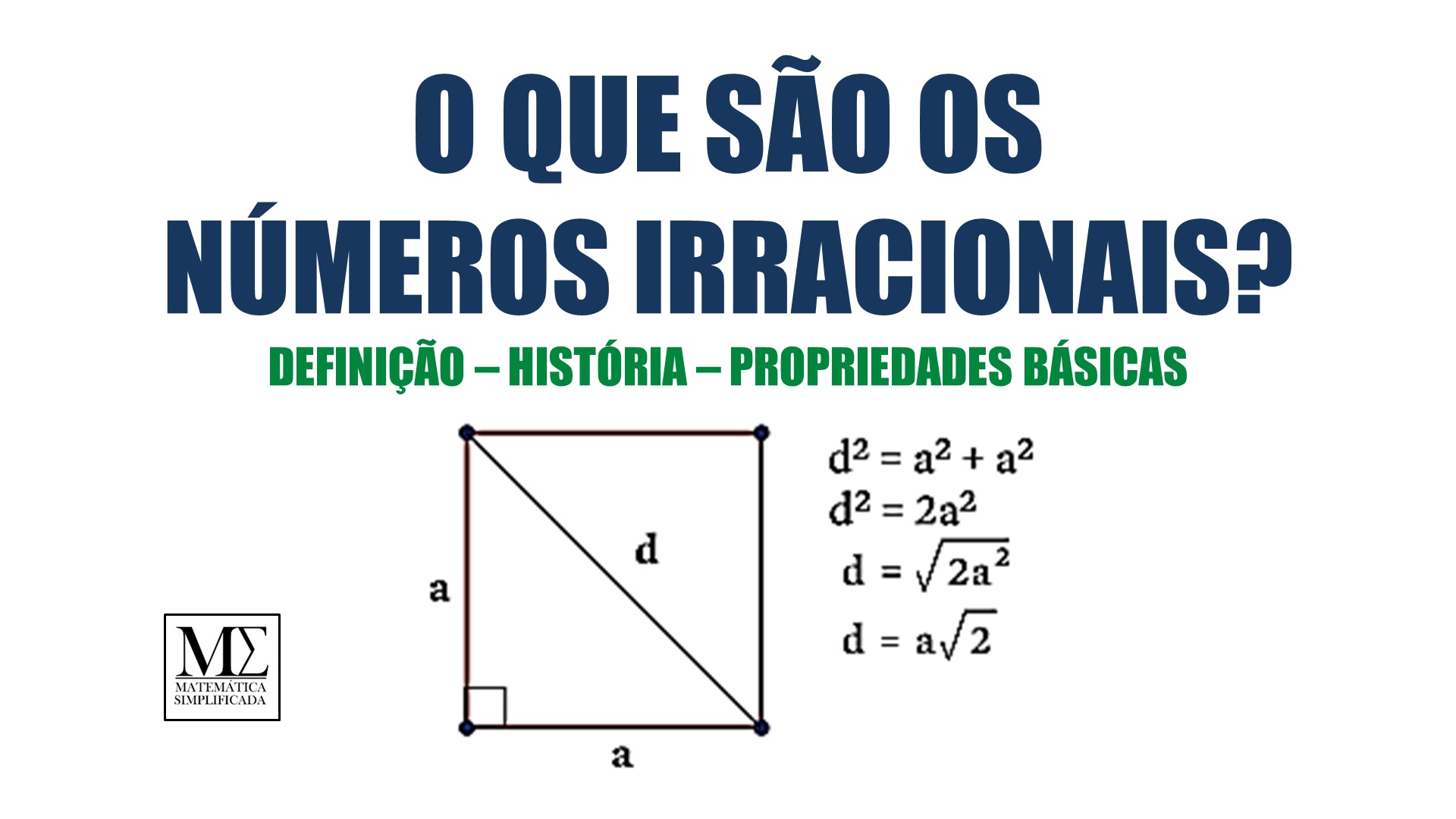
3. Os números \sqrt{2} = 1,4142136... , \sqrt{3} = 1,7320508... e \pi = 3,141592... por não apresentarem representação infinita periódica, também são números irracionais.
4. A proporção áurea, ou número de ouro, ou número áureo, ou ainda proporção dourada é um número irracional denotada pela letra grega φ (phi) e com o valor arredondado a três casas decimais de 1,618 e matematicamente pode ser escrito como $$ \Phi = \frac{1 + \sqrt{5}}{2}. $$

Obviamente existem outro números irracionais obtidos de modo bem mais complexo do que simplesmente extrair raízes não inteiras de números positivos ou mesmo resolver equações algébricas com coeficientes inteiros, como no caso de \pi e \Phi .

Um exemplo disso é o número e , um irracional que determina a base de uma importante função exponencial e que pode ser escrito como o limite de uma sequência de números reais$$e = \lim_{n \rightarrow \infty}{\left( 1 + \frac{1}{n}  \right)^n} = 2.71828182846…$$ Este limite resultado determina um importante limite envolvendo funções exponenciais, chamado de 2º Limite Fundamental.

Os números irracionais satisfazem as seguintes propriedades:

1. A soma de dois irracionais é também um irracional.

2. A soma de um irracional e um racional é um irracional.

3. O produto de um irracional por um racional é sempre um irracional

4. O produto de dois irracionais nem sempre é um irracional.

A Raíz Quadrada de 2 é Irracional

Vamos mostrar que o número \sqrt{2} não pode ser escrito como uma fração. De fato. Suponha que existam inteiros p,q tais que \sqrt{2}=\dfrac{p}{q} e mdc(p,q)=1.

Assim, p^2 = 2 q^2, ou seja, p^2 é par. Logo p é par (se p fosse ímpar, p^2 seria ímpar), digamos p=2r. Daí, $$p^2=4r^2=2q^2 \Rightarrow 2r^2 = q^2.$$

Analogamente, q^2 par, implica q ser par. Portanto, tanto p quanto q são pares, assim sendo, mdc(p,q)=2. O que é contra-hipótese.

Portanto, \sqrt{2} não pode ser escrito como uma fração, logo é irracional. Em geral, \sqrt{m} não é racional para qualquer número primo m .

Os Números Irracionais ao longo da História da Matemática.

Os números irracionais começam a aparecer na matemática pelos estudos realizados na Grécia Antiga quando, ao calcular-se problemas envolvendo o teorema de Pitágoras, encontrava-se raízes não exatas.

O ato de procurar solução para essas raízes não exatas tornou notável a existência das dízimas não periódicas, ou seja, de números cuja parte decimal é infinita e não possui uma sequência bem definida

À época, a saída usada por Pitágoras foi, então, proclamar que alguns comprimentos simplesmente não poderiam ser expressos através de números, contrariando sua filosofia que dizia que o número é o principio de tudo e cujos seguidores eram chamados de pitagóricos. paradoxo foi mantido rigorosamente em sigilo dentro da sociedade pitagórica.

Isto gerou uma lenda a respeito da sociedade pitagórica que torna muito curiosa a história dos números irracionais. Segundo a lenda, Hipaso de Metaponto, um seguidor de Pitágoras, misteriosamente, ou convenientemente, morreu afogado após ter falado um pouco demais. Apesar disso, a descoberta dos números irracionais, que ameaçava a doutrina de que tudo podia ser demonstrado através de números, é comumente atribuída a Hipaso.

Historicamente, os números irracionais começaram a ser descobertos pelos gregos, mas os hindus também estudaram estes números e foram os primeiros a considerar as raízes irracionais dos números como números, de fato. Isso porque eles não levavam a sério a diferença entre grandeza comensuráveis e incomensuráveis.

No passado, para a matemática indiana liderada por Brahmagupta não havia dificuldade em aceitar os números irracionais como foram para os gregos e as gerações posteriores seguiram seu exemplo sem análise crítica, até que os matemáticos do século XIX estabeleceram o sistema de números reais sobre base sólida.

Na primeira metade do século XVI a matemática viu a álgebra alemã ganhar força, e um dos principais matemáticos do período foi Michael Stifel (1487-1567) que ofereceu uma definição interessante para os números irracionais. Um tanto hesitante, ele dizia que estes números estão “escondidos sob uma espécie de nuvem de infinitude”.

No século seguinte, Cardano, em sua “Ars Magna”, observou pela primeira vez de modo significativo os números irracionais, que àquela altura eram bem aceitos por causa das aproximações com números racionais que eram possíveis de serem feitas. Mesmo assim, naquele período, números negativos, irracionais e imaginários (complexos) eram considerados anomalias com as quais os matemáticos tinha que conviver.

Um nome importante na história da matemática para os números irracionais foi Georg Cantor, um explorador do infinito na matemática e o primeiro a perceber que os conjuntos finitos não são todos iguais e se dispôs a construir uma hierarquia de conjuntos infinitos. Seus estudos sobre os conjuntos numéricos levaram a uma aritmética transfinita e a estabelecer a teoria dos conjuntos como uma disciplina matemática completamente desenvolvida. Por consequência, organizava, enfim, o conjunto dos números irracionais dentro de seu contexto nos números reais.

Observações Topológicas Sobre o Conjunto dos Números Irracionais

A topologia da reta real tem como objetivo definir com clareza vários subconjuntos úteis de números reais, e explorar suas propriedades. Abaixo estão algumas das principais propriedades topológicas do conjunto dos números irracionais com um conjunto denso nos números reais.

(a) Todo intervalo aberto contém um número irracional. Ou seja, os números irracionais estão espalhados por toda parte dentro do conjunto dos números reais;

(b) Todo intervalo aberto contém um número infinito de números irracionais. E ainda podemos mostrar que existem mais números irracionais do que racionais. Isso porque o conjunto dos números racionais é enumerável (possui a mesma cardinalidade dos números naturais) enquanto os irracionais é um conjunto não-enumerável.

(c) Qualquer número real é ponto de acumulação do conjunto dos números irracionais. Isso se dá uma particularidade dos números racionais. A insuficiência mais grave dos números racionais é o fato de que alguns conjuntos limitados de números reais não possuem supremo ou ínfimo (entenda este conceito topológico neste artigo). Este fato está ligado à inexistência de raízes quadradas  racionais de certos números inteiros como Pitágoras e seus discípulos descobriram.

Leia Mais:

• Números Reais | Introdução à Topologia da Reta Real
• Números Reais | Definição, Operações Elementares, Intervalos e Módulo
• Números Racionais | Definição, Propriedades e Operações Elementares
• Números Complexos | Primeiras Definições e Operações Elementares