Maximos e Mínimos: O Método dos Multiplicadores de Lagrange

O Método dos Multiplicadores de Lagrange é um elegante artifício usado para encontrar máximos e mínimos condicionados para os campos escalares, que são funções de várias variáveis a valores reais, em geral, dadas na forma f: A \subset \mathbb{R} ^n\rightarrow \mathbb{R}, que associa a cada n-upla de \mathbb{R} ^n um escalar.

Em muitas aplicações o problema de achar os extremos de uma função apresenta-se sujeito a certas condições nas variáveis independentes, que são chamadas de vínculo e o problema correspondente é um problema de extremos condicionados.

Razões de ordem prática justificam a procura de um novo método de resolver problemas de extremos condicionados. Entretanto, também existem razões de ordem teórica que são as que melhor justificam o engenhoso Método dos Multiplicadores de Lagrange que queremos apresentar neste artigo.

Vamos apresentar esse conceito através de funções com domínio no \mathbb{R} ^2 simplesmente pela facilidade em estabelecer gráficos e representações do domínio, e também por serem as funções que mais aparecem em aplicações de engenharia, por exemplo.

O Método dos Multiplicadores de Lagrange: Máximos e Mínimos Condicionados

Nosso objetivo agora é estudar os extremantes locais de uma função f diferenciável num conjunto aberto A do \mathbb{R} ^2 ou \mathbb{R}^3 sobre conjuntos do tipo \{ (x,y); g(x,y)=0 \}, \{ (x,y,z); g(x,yz)=0 \} ou \{ (x,y,z); g(x,yz)=0\;\;e\;\;h(x,yz)=0 \}.

EXEMPLO

Encontrar os pontos extremantes de f(x,y) = 3x+2y com a restrição x^2+y^2=1.

Ou seja, queremos encontrar os pontos de máximo ou mínimo da função f(x,y) tais que (x,y) estejam na circunferência centrada na origem e com raio igual a 1. Neste caso, nossa função esta sob o conjunto \{ (x,y); x^2+y^2-1=0 \}.

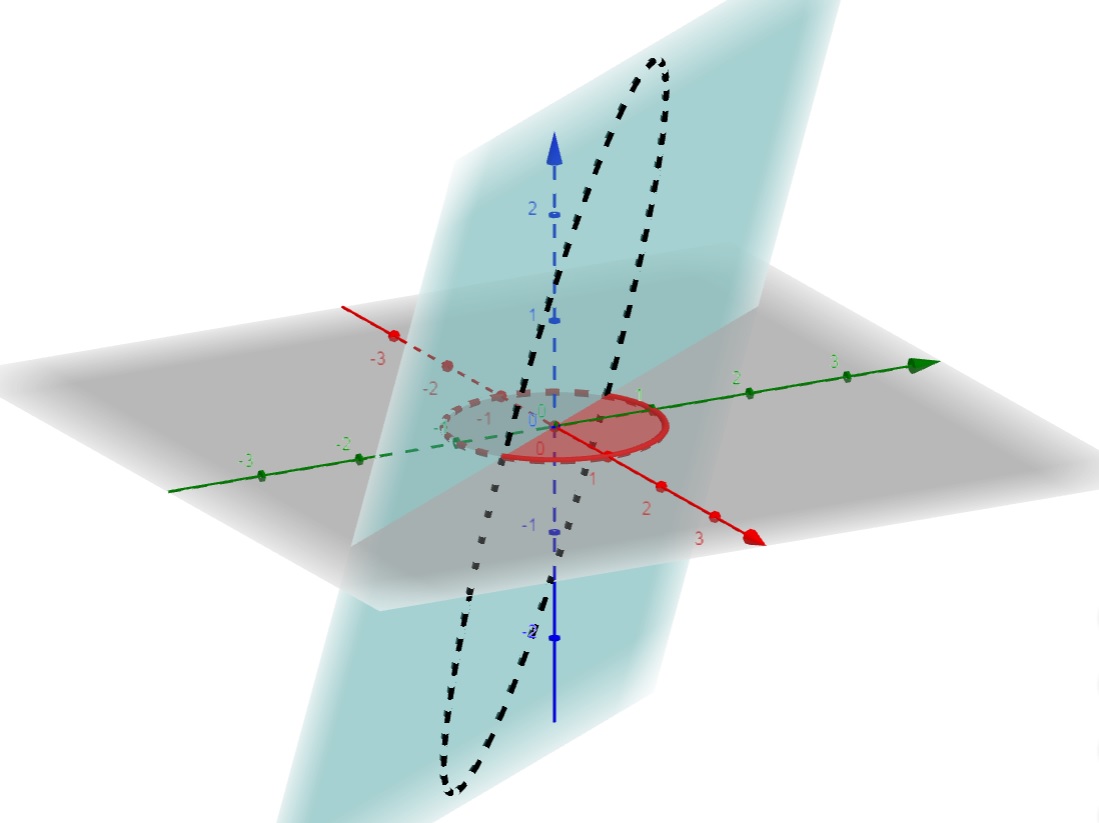
Acima, temos uma ilustração do nosso problema. Em vermelho, sobre o plano xOy, está o círculo, onde consideramos apenas a fronteira \{ (x,y); x^2+y^2-1=0 \}. Colocamos tracejado, sobre o plano  f(x,y) = 3x+2y a imagem desta função restrita a esta fronteira. Pode-se perceber que, de fato, termos um ponto de máximo e um ponto de mínimo.

Para este estudo utilizamos o Método dos Multiplicadores de Lagrange que é dado pelo teorema a seguir.

TEOREMA [Multiplicadores de Lagrange]

Seja f(x,y) diferenciável no aberto A e seja B = \{ (x,y); g(x,y)=0 \}, onde g é diferenciável e possui derivadas parcias contínuas em A e \nabla g(x,y) \neq (0,0), \forall (x,y) \in B. Uma condição necessária para que (x_0,y_0) seja extremante local de f em B é que exista um real \lambda tal que $$\nabla f(x_0, y_0) = \lambda _0 \nabla g(x_0, y_0).$$

EXEMPLO

Encontrar os pontos extremantes de f(x,y) = 3x+2y com a restrição x^2+y^2=1.

Podemos notar sem dificuldade que a função g(x,y)=x^2+y^2 -1 é diferenciável e possui derivadas parciais contínuas, assim os extremantes locais satisfazem o sistema

$$\left\{ \begin{array}{rll}
\nabla f(x, y) & = & \lambda \nabla g(x , y)\\
g(x,y) & = & 0
\end{array} \right. = \left\{ \begin{array}{lll}
(3, 2) & = & \lambda (2x , 2y)\\
x^2+y^2-1 & = & 0
\end{array} \right.$$

Da primeira linha do sistema, temso que $$x=\frac{3}{2 \lambda}\;\;\;e\;\;\;y=\frac{1}{\lambda}$$

Substituindo estes valores na segunda linha do sitema, obtemos $$ \left( \frac{3}{2 \lambda} \right)^2+ \left( \frac{1}{\lambda} \right)^2 = 1 \Rightarrow \lambda = \pm \frac{\sqrt{13}}{2} .$$

Assim, com o valor de \lambda obtemos dois pontos: $$\left( \frac{3\sqrt{13}}{13} , \frac{2\sqrt{13}}{13} \right)\;\;\; e \;\;\; \left( – \frac{3\sqrt{13}}{13} , – \frac{2\sqrt{13}}{13} \right).$$ Estes são os extremantes locais da função f restrita à g(x,y) = 0.

Um ótimo exercício é classificar os pontos extremantes encontrados no exemplo acima.

OBSERVAÇÃO

Podemos garantir, para uma função f(x,y,z) diferenciável no aberto A \in \mathbb{R} ^3 e para um conjunto B = \{ (x,y,z); g(x,y,z)=0 \}, onde g é diferenciável e possui derivadas parcias contínuas em A e \nabla g(x,y,z) \neq (0,0,0), \forall (x,y,z) \in B, a existencia de um \lambda _0 que satisfaz a relação $$\nabla f(x_0, y_0, z_0) = \lambda _0 \nabla g(x_0, y_0,z_0)$$ para um extremante local (x_0, y_0, z_0) de f.

INTERPRETAÇÃO GEOMÉTRICA

Uma interpretação geométrica das equações $$\nabla f(x, y,z) = \lambda \nabla g(x, y,z)$$ $$ g(x, y, z) = 0 $$ se faz interessante neste momento.

Note-se que a equação f(x,y,z) = k descreve uma superfície para cada valor do parâmetro k. Considerando-se diferentes valores de k, obtemos toda uma família de superfícies que cobrem certa região do espaço conforme vemos na figura abaixo:

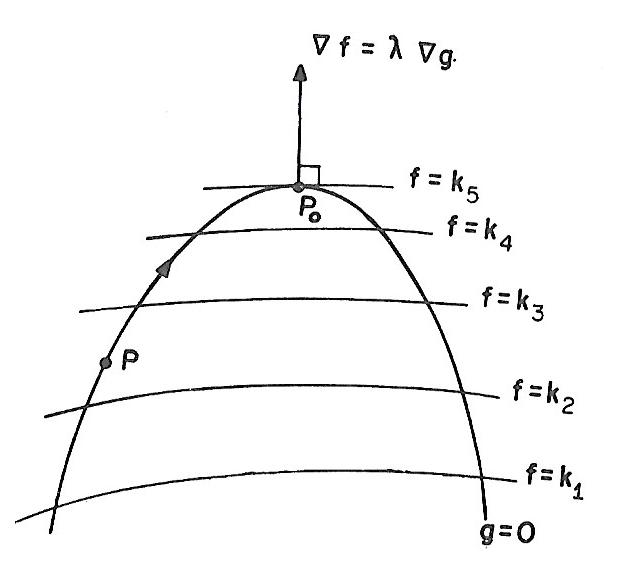
O problema de encontrar o máximo ou o mínimo de f , com a condição g = 0 , consiste em achar, dentre as superfícies da família f = k que cortam a superfície g = 0 , aquela que corresponde ao maior ou ao menor valor de k, respectivamente. Quando isso ocorrer as superfícies f = k e g = 0 se tocarão tangencialmente, tendo a mesma reta normal num mesmo ponto extremante, isto é, os vetores \nabla f que cortam a superfície \nabla g terão a mesma direção quando aplicados neste ponto.

EXEMPLO

Determine o ponto da superfície x^2+2y^2+z^2=1 cuja soma das coordenadas seja máxima.

Queremos maximizar a função f(x,y) = x+y+z sujeito a restrição g(x,y,z)=x^2+2y^2+z^2-1.

Assim,

$$\left\{ \begin{array}{rll}
\nabla f(x, y, z) & = & \lambda \nabla g(x , y, z)\\
g(x,y,z) & = & 0
\end{array} \right. = \left\{ \begin{array}{lll}
(1, 1, 1) & = & \lambda (2x , 4y, 2z)\\
x^2+2y^2-1+z^2 & = & 0
\end{array} \right.$$

Da primeira linha do sistema obtemos $$x=y=\frac{1}{2 \lambda} \;\;\;e\;\;\;z=\frac{1}{4 \lambda}$$ e substituindo na segunda linha do sistema ficamos com $$\frac{5}{8\lambda ^2} =1 \Rightarrow \lambda = \pm \frac{\sqrt{10}}{4}.$$ Portanto, os pontos (\frac{\sqrt{10}}{5} , \frac{\sqrt{10}}{10}, \frac{\sqrt{10}}{5}) e (-\frac{\sqrt{10}}{5} , -\frac{\sqrt{10}}{10}, -\frac{\sqrt{10}}{5}) são os candidatos a extremantes locais de f. Como (\frac{\sqrt{10}}{5} , \frac{\sqrt{10}}{10}, \frac{\sqrt{10}}{5}) é ponto de máximo (Exercício!!!) temos que o ponto da superfície x^2+2y^2+z^2=1 cuja soma das coordenadas é máximo é o ponto (\frac{\sqrt{10}}{5} , \frac{\sqrt{10}}{10}, \frac{\sqrt{10}}{5}).

Agora queremos uma condiçao necessária para que (x_0,y_0,z_0) seja um extremante local de f(x,y,z) com as restrições g(x,y,z) = 0 e h(x,y,z)=0.

Esta condição é dada pelo próximo teorema.

TEOREMA

Seja f(x,y,z) diferenciável no aberto A \subset \mathbb{R}^3 e seja B = \{ (x,y,z); g(x,y,z)=0\;\;\; e\;\;\; h(x,y,z) = 0 \}, onde g e h são diferenciáveis e possuem derivadas parcias contínuas em A e \nabla g(x,y,z) \wedge \nabla h(x,y,z) \neq (0,0,0), \forall (x,y.z) \in B. Uma condição necessária para que (x_0,y_0,z_0) seja extremante local de f em B é que existam reais \lambda _1 e \lambda _2 tais que $$\nabla f(x_0, y_0, z_0) = \lambda _1 \nabla g(x_0, y_0, z_0) + \lambda _2 \nabla h(x_0, y_0, z_0).$$

EXEMPLO

Determine os pontos mais afastados da origem cujas coordenadas estão sujeitas às equações x^2+4y^2+z^2=4 e x+y+z=1.

Queremos maximizar a função $$f(x,y) = x^2+y^2+z^2$$ condicionado a g(x,y,z) = x+y+z -1 e h(x,y,z) = x^2+y^2+z^2-4.

O conjunto A = \mathbb{R}^3 e o conjunto B = \{ (x,y,z); x+y+z -1=0\;\;\; e\;\;\; x^2+4y^2+z^2-4 = 0 \}.

Daí

• \nabla g(x,y,z) = (1,1,1) e \nabla h(x,y,z) = (2x,8y,2z)
• \nabla g(x,y,z)\wedge \nabla h(x,y,z) = (2z-8y, 2x-2z, 8y-2x) \neq (0,0,0) em B

Os candidatos a extremantes locais são dados pelo sistema

$$\left\{ \begin{array}{rll}
\nabla f(x, y, z) & = & \lambda_1 \nabla g(x , y, z) + \lambda_2 \nabla g(x , y, z)\\
g(x,y,z) & = & 0\\
h(x,y,z) & = & 0
\end{array} \right. = $$ $$ = \left\{ \begin{array}{lll}
(2x, 2y, 2z) & = & \lambda_1 (1,1,1)+ \lambda_2(2x , 8y, 2z)\\
x+y+z -1 & = & 0\\
x^2+4y^2+z^2-4 & = & 0
\end{array} \right. = $$ $$ = \left\{ \begin{array}{lll}
2x & = & \lambda_1 + 2x \lambda_2 \\
2y & = & \lambda_1 + 8y \lambda_2 \\
2z & = & \lambda_1 + 2z \lambda_2 \\
x+y+z -1 & = & 0\\
x^2+4y^2+z^2-4 & = & 0
\end{array} \right. = $$ $$= \left\{ \begin{array}{lll}
2x(1-\lambda_2) & = & \lambda_1 (1)\\
2y(1-4 \lambda_2) & = & \lambda_1 (2)\\
2z (1-\lambda_2) & = & \lambda_1 (3)\\
x+y+z -1 & = & 0 (4)\\
x^2+4y^2+z^2-4 & = & 0 (5)
\end{array} \right. = $$

de (1) e (3) segue que x=z para \lambda_2 \neq 1, e substituindo em (4) e (5) obtemos

$$\left\{ \begin{array}{lll}
2x+y & = & 1\\
2x^2+4y^2 &= & 4
\end{array} \right. \Rightarrow \left\{ \begin{array}{lll}
y & = & 1 – 2x\\
2x^2+4y^2 &= & 4 \end{array} \right.$$

Daí, x=0 ou x=\frac{8}{9}, ou seja, os candidatos a pontos extremantes são (0,1,0) e \left(\frac{8}{9}, -\frac{7}{8}, \frac{8}{9} \right)

Para \lambda_2 = 1 teremos \lambda_1 = 0 e, daí, segue que y=0. Substituindo em (4) e em (5) teremos o sistema

$$\left\{ \begin{array}{lll}
x+z & = & 1\\
x^2+z^2 &= & 4
\end{array} \right. \Rightarrow \left\{ \begin{array}{lll}
z & = & 1 – x\\
x^2+z^2 &= & 4 \end{array} \right.$$, assim x= \frac{1 \pm \sqrt{7}}{2}, ou seja, os candidatos a pontos extremantes são \left(\frac{1 + \sqrt{7}}{2}, 0, \frac{1 - \sqrt{7}}{2} \right) e \left(\frac{1 - \sqrt{7}}{2}, 0, \frac{1 + \sqrt{7}}{2} \right).

Agora, substituindo os quatro pontos extremantes na função f(x,y) obtemos $$f(0,1,0)=1,$$ $$f\left(\frac{1 + \sqrt{7}}{2}, 0, \frac{1 – \sqrt{7}}{2} \right)=4, $$ $$f\left(\frac{1- \sqrt{7}}{2}, 0, \frac{1 + \sqrt{7}}{2} \right)=4, $$ e $$f\left(\frac{8}{9}, -\frac{7}{8}, \frac{8}{9} \right)=\frac{171}{81}<3 .$$ Portanto, os pontos \left(\frac{1 + \sqrt{7}}{2}, 0, \frac{1 - \sqrt{7}}{2} \right) e \left(\frac{1 - \sqrt{7}}{2}, 0, \frac{1 + \sqrt{7}}{2} \right) são os pontos mais distantes da origem.

Exercícios Resolvidos Sobre Multiplicadores de Lagrange

• Multiplicadores de Lagrange – 1ª Lista de Exercícios Resolvidos
• Multiplicadores de Lagrange – 2ª Lista de Exercícios Resolvidos
• Multiplicadores de Lagrange – 3ª Lista de Exercícios Resolvidos

Leia Mais:

• Máximos e Mínimos de Funções de Várias Variáveis
• Derivadas Parciais | Funções de Várias Variáveis a Valores Reais
• Limite e Continuidade de Funções de Várias Variáveis Reais
• Funções de Várias Variáveis Reais a Valores Reais ou Campos Escalares

Assista Nossa Video Aula: