Limite e Continuidade de Funções Vetoriais de Várias Variáveis.

Nesse artigo queremos apresentar a ideia de limite e continuidade para as funções vetoriais de várias variáveis..

Sejam m e n dois naturais diferentes de zero.

Uma função de n variáveis reais a valores vetoriais em \mathbb{R}^m é uma função f:A\rightarrow \mathbb{R}^m, onde A é um subconjunto não vazio de \mathbb{R}^n, denominado domínio de f.

Esta função associa cada n-upla ordenada (x_1,x_2, ..., x_n) \in A a um único vetor f(x_1,x_2, ..., x_n) \in \mathbb{R}^m.

O conjunto $$\left\{ f(x_1,x_2, …, x_n) \in \mathbb{R}^m; (x_1,x_2, …, x_n) \in A \right\}$$ é denominado imagem de f.

Abaixo vamos definir o limite e a continuidade de funções vetoriais de várias variáveis com domínio no \mathbb{R} ^3 simplesmente pela facilidade em estabelecer gráficos e representações do domínio, e também por serem as funções que mais aparecem em aplicações de engenharia, por exemplo.

A Topologia dos Espaços R² e R³

Antes da definição de limites para funções de duas ou mais variáveis se faz necessária a definição de alguns conceitos básicos quanto a topologia dos espaços \mathbb{R} ^2 e \mathbb{R} ^3.

DEFINIÇÃO (Vizinhança ou Bola Aberta)

Dado um ponto P_0 \in \mathbb{R}^n e um número \delta >0, denominamos de vizinhança de P_0, que se indica por V_{\delta} (P_0 ), ou bola aberta B \left( P_0 , \delta \right) , ao conjunto de pontos P \in \mathbb{R}^n, cuja distância a P_0 seja menor do que \delta.

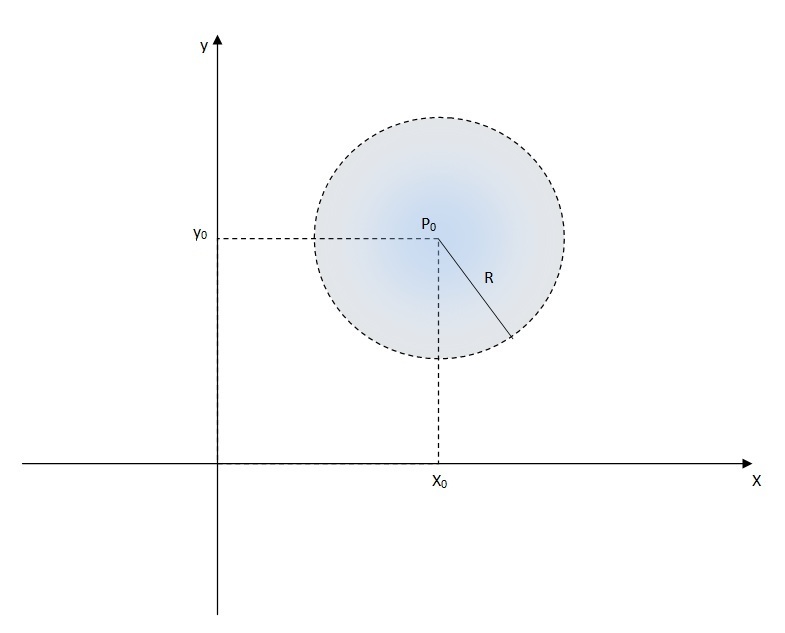
Ou seja, no \mathbb{R} ^2,

$$B \left( P_0 , \delta \right) = \left\{ (x,y) \in \mathbb{R}^2 ; \| (x,y) – (x_0, y_0) \| < \delta \right\}.$$

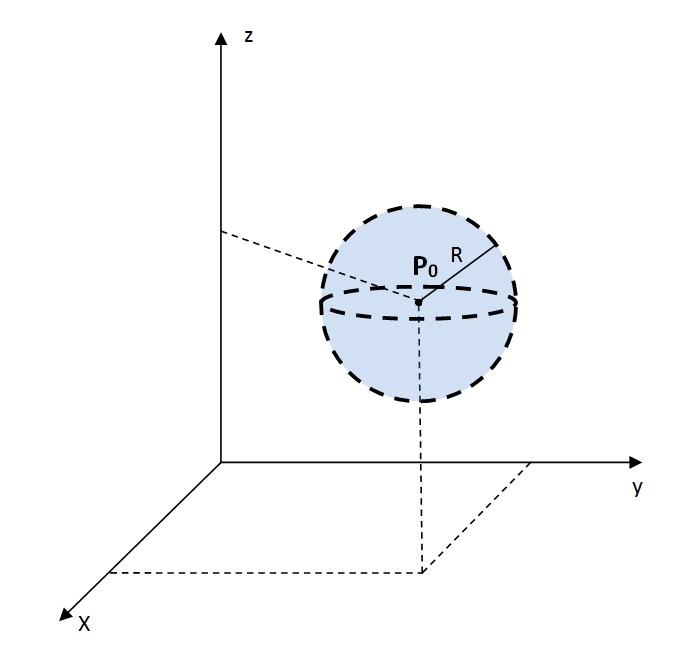
No caso do espaço \mathbb{R} ^3 a vizinhaça de V_{\delta} (P_0), ou a bola aberta B(P_0, \delta), para um ponto P_0 (x_0,y_0,z_0) é definida pela condição

$$B \left( P_0 , \delta \right) = \left\{ (x,y,z) \in \mathbb{R}^3 ; \| (x,y,z) – (x_0, y_0,z_0) \| < \delta \right\}.$$

EXEMPLO

O conjunto abaixo representa a vizinhança dos pontos do plano que distam menos de 1 da origem.

\begin{eqnarray*}
B \left( (0,0) , 1 \right) & = & \left\{ (x,y) \in \mathbb{R}^2 ; \| (x,y) – (0, 0) \| < 1 \right\}\\
\\
& = & \left\{ (x,y) \in \mathbb{R}^2 ; \| (x,y) \| < 1 \right\}\\
\\
& = & \left\{ (x,y) \in \mathbb{R}^2 ; \sqrt{x^2 +y^2} < 1 \right\}\\
\\
& = & \left\{ (x,y) \in \mathbb{R}^2 ; x^2 +y^2 < 1 \right\}\\
\end{eqnarray*}

Já o conjunto de pontos que distam menos que 1 do ponto (1,0,1) está escrito abaixo:

\begin{eqnarray*}
B \left( (1,0,1) , 1 \right) & = & \left\{ (x,y,z) \in \mathbb{R}^3 ; \| (x,y,z) – (1,0, 1) \| < 1 \right\}\\
\\
& = & \left\{ (x,y,z) \in \mathbb{R}^3 ; \| (x-1,y,z-1) \| < 1 \right\}\\
\\
& = & \left\{ (x,y,z) \in \mathbb{R}^3 ; \sqrt{(x-1)^2 +y^2 + (z-1)^2} < 1 \right\}\\
\\
& = & \left\{ (x,y) \in \mathbb{R}^3 ; (x-1)^2 +y^2+(z-1)^2 < 1 \right\}\\
\end{eqnarray*}

DEFINIÇÃO (Ponto de Acumulação)

Seja A \subset \mathbb{R} ^n. Um ponto P \in \mathbb{R} ^n é dito um ponto de acumulação de A se toda bola aberta com centro em P contiver uma infinidade de pontos de A.

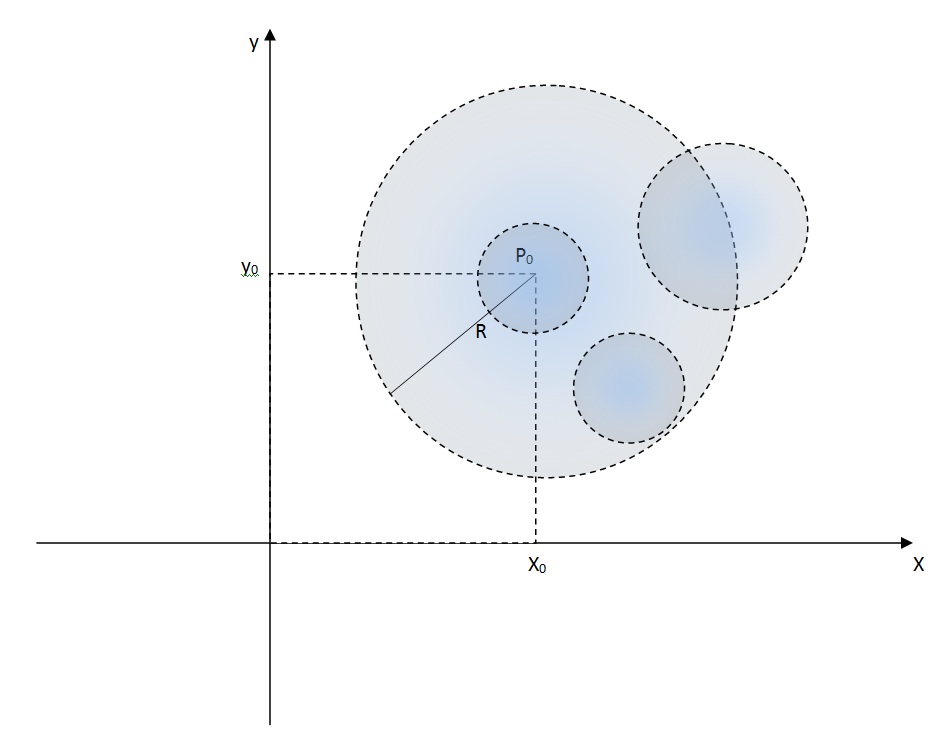
EXEMPLO

Seja A=\left\{ (x,y) \in \mathbb{R}^2; 0< \sqrt{(x-1)^2+(y-2)^2}\right\}<1.

Então,

• todos os pontos de A são pontos de acumulação de A.
• Os pontos da circunferência (x-1)^2+(y-2)^2 = 1 também não pertence a A, mas são pontos de acumulação de A.
• Qualquer ponto (x,y) do plano tal que (x-1)^2+(y-2)^2 > 1 não é ponto de acumulação de A.

O Limite de Uma Função Vetorial de Várias Variáveis

Vamos definir o limite de uma função vetorial de várias variáveis para um campo vetorial de dimensão 3 para que fique mais fácil a sua visualização. Porem, esta mesma ideia pode ser estendida para uma função f:A \subset \mathbb{R}^n \rightarrow \mathbb{R}^m, usando o conceito topológico de bolas abertas e pontos de acumulação em cada um destes conjuntos.

DEFINIÇÃO

Seja P_0(x_0, y_0, z_0) um ponto de um domínio D e \vec{r_0} seu vetor posição. Seja \vec{f} uma função vetorial definida em D, exceto, possivelmente, em \vec{r_0} . Seja \vec{a} =  a_1 \vec{i} + a_2 \vec{j} + a_3 \vec{k} um vetor constante. Se \vec{r} é o vetor posição do ponto P_0(x_0, y_0, z_0), dizemos que $$\lim_{\vec{r} \rightarrow \vec{r_0}}{\vec{f} (x,y,z)} = \vec{a} $$ se, para todo \varepsilon >0 , existe \delta > 0 tal que $$ \left| \vec{f} (x,y,z) – \vec{a} \right| < \varepsilon \Rightarrow  \left| \vec{r} – \vec{r_0} \right| < \delta.$$

Essa definição pode ser ilustrada pela imagem abaixo:

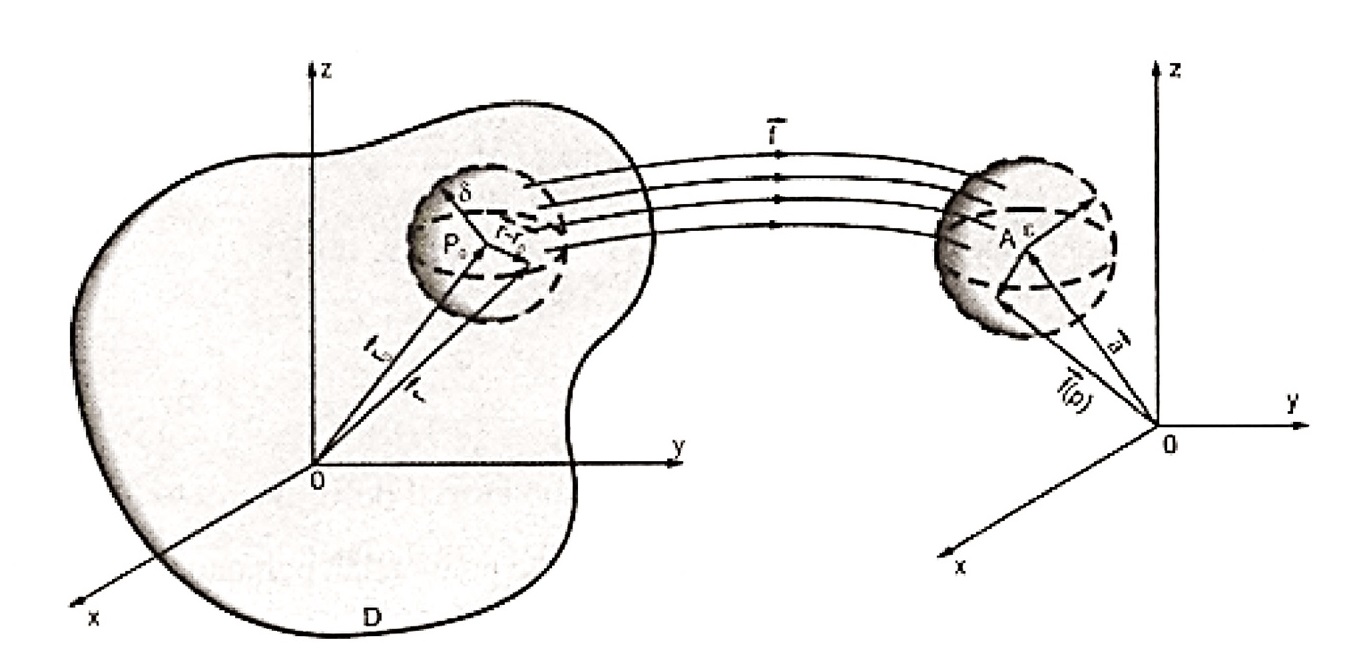
A ideia básica para $$\lim_{\vec{r} \rightarrow \vec{r_0}}{\vec{f} (x,y,z)} = \vec{a} $$ seria a de que para toda bola aberta centrada no ponto a = a_1 \vec{i} + a_2 \vec{j} + a_3 \vec{k} e com raio \varepsilon >0 no contradomínio de \vec{f} , existe uma bola aberta centrada P_0(x_0, y_0, z_0) e com raio igual  \delta > 0 no domínio de \vec{f} , tal que todo ponto da bola aberta no domínio é levado pela \vec{f} num ponto da bola aberta no contra-domínio.

De forma análoga ao que fizemos para as funções vetoriais de uma variável, se \vec{f} = (f_1, f_2, f_3) , onde cada f_i, i = 1,2,3 é uma função escalar de várias variáveis, então $$\lim_{(x,y,z) \rightarrow (x_0, y_0, z_0)}{\vec{f} (x,y,z)} = \vec{a} \Leftrightarrow \lim_{(x,y,z) \rightarrow (x_0, y_0, z_0)}{f_i (x,y,z)} = a_i , $$ onde i = 1,2,3 .

Ou seja, o limite de uma função vetorial de várias variáveis existe, se, e somente se, o limite de cada uma funções componentes existe.

PROPRIEDADES DO LIMITE

As propriedades do limite de uma função vetorial de várias variáveis seguem as mesmas daquelas enumeradas para as funções vetoriais de uma variável dadas neste artigo sobre o conceito do limite de curvas.

EXEMPLOS:

1) \lim_{(x,y) \rightarrow (0,0)}{ [y \vec{i} - x \vec{j} ]} = \lim_{(x,y) \rightarrow (0,0)}{ y \vec{i}} -  \lim_{(x,y,z) \rightarrow (0,0)}{ x \vec{j} } = \vec{0}.

2) \lim_{(x,y,z) \rightarrow (1,2,1)}{ \left( e^{x-1}, \dfrac{y(x-1)}{x^2-1}, 3xyz \right)} =  \left( \lim_{(x,y,z) \rightarrow (1,2,1)}{e^{x-1}}, \lim_{(x,y,z) \rightarrow (1,2,1)}{\dfrac{y(x-1)}{x^2-1}}, \lim_{(x,y,z) \rightarrow (1,2,1)}{3xyz} \right) = (1,1,3)

A Continuidade de Uma Função Vetorial de Várias Variáveis

Novamente, vamos definir a continuidade de uma função vetorial de várias variáveis para um campo vetorial de dimensão 3 para que fique mais fácil a sua visualização.

Porem, esta mesma ideia pode ser estendida para uma função f:A \subset \mathbb{R}^n \rightarrow \mathbb{R}^m, usando o conceito topológico de bolas abertas e pontos de acumulação em cada um destes conjuntos, como geralmente é feito em livros de Análise no \mathbb{R} ^n .

DEFINIÇÃO (CONTINUIDADE DA FUNÇÃO VETORIAL)

Seja \vec{f} (x,y,z) , definida num domínio D. Dizemos que \vec{f} é contínua em P_0(x_0, y_0, z_0) \in D, se $$\lim_{(x,y,z) \rightarrow (x_0, y_0, z_0)}{\vec{f} (x,y,z)} = \vec{f} (x_0,y_0,z_0). $$

Se \vec{f} é contínua em cada ponto do domínio D, dizemos que ela é contínua em D.

Como era de se esperar, assim como para as funções vetoriais de uma variável, \vec{f} é contínua em cada ponto do domínio D se, e somente, cada uma de suas funções componentes também é contínua em D.

EXEMPLO:

1) A função vetorial \vec{f} (x,y) = y \vec{i} - x \vec{j}  é contínua em todos os pontos do plano.

2) Já a função \vec{f} (x,y,z) = \left( e^{x-1}, \dfrac{y(x-1)}{x^2-1}, 3xyz \right) é contínua em todos os ponto do espaço \mathbb{R}^3 tais que x \pm 1 .

3) A função vetorial f(u,v) = (u, v, u^2 + v^2) é contínua em todos os pontos do plano. É interessante observar que a imagem desta função descreve uma superfície no espaço que é um paraboloide.

4) Considere o campo vetorial $$\vec{F}(x,y) = – \frac{\vec{r}}{\| r \|^2},$$ onde \vec{r}= x\vec{i} + y \vec{j}. Observe que este campo vetorial é dado por $$\vec{f}(x,y) = – \left( \frac{x}{x^2 + y^2}, \frac{y}{x^2 + y^2} \right),$$ que é contínuo em todos os pontos do plano, exceto a origem.

Observe que se você escrevê-lo em temos de coordenadas polares, o mesmo se mantém, pois considerando x = r cos \theta e y = r sen \theta , obtemos $$\vec{F}(r, \theta) = – \left( \frac{cos ( \theta )}{r}, \frac{sen ( \theta )}{r} \right),$$ que será contínua para todos os pontos do plano, exceto onde r = 0, ou seja, na origem.

Leia Mais:

• Limite e Continuidade de Funções de Várias Variáveis Reais
• Funções de Variáveis Complexas | Limite e Continuidade
• Curvas | Limite e Continuidade de uma Função Vetorial
• Funções Vetoriais de Várias Variáveis | Transformações Lineares
• Funções Vetoriais de Várias Variáveis | O que são Campos Vetoriais?
• EFEITO BORBOLETA | Edward Lorenz e a Teoria do Caos
• Os Espaços Euclidianos R² e R³ | Cálculo de Várias Variáveis
• GRÁFICOS | Da Análise Estatística ao Mercado de Ações