Integral de Linha de 1ª e 2ª Espécies, e o Teorema de Green no Plano

Vamos estabelecer de foma simples e direta a Integral de Linha de Primeira e Segunda Espécie, além de enunciar e aplicar o Teorema de Green no Plano. Além das integrais múltiplas trabalhadas neste artigo sobre integrais duplas e neste artigo sobre integrais triplas. As Integrais de Linha e de superfície são outras formas importantes de se estender a noção de integral.

Em geral, integrais deste tipo aparecem quando consideramos distribuições lineares de massa ou carga elétrica e o trabalho de uma força, por exemplo. Geralmente, integrais de linha que envolvem integrais complicadas podem ser calculadas utilizando métodos numéricos ou métodos gráficos.

Curvas Orientadas

Se um ponto material desloca-se sobre uma curve suave C, temos dois possíveis sentidos de percurso. A escolha de um deles como sentido positivo, define uma orientação na curva C.

Suponhamos que a curva C seja representada por f(t)=(x(t), y(t),z(t)); t \in [a,b] , convencionamos chamar de sentido positivo sobre C, o sentido no qual a curva é traçada quando o parâmetro t cresce da a até b. O sentido oposto é chamado de sentido negativo sobre C.

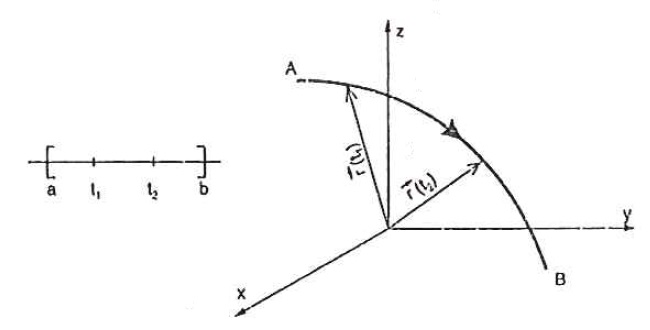
Por esta definição, o sentido positivo de uma curva orientada é o sentido dos valores crescentes do parâmetro t.

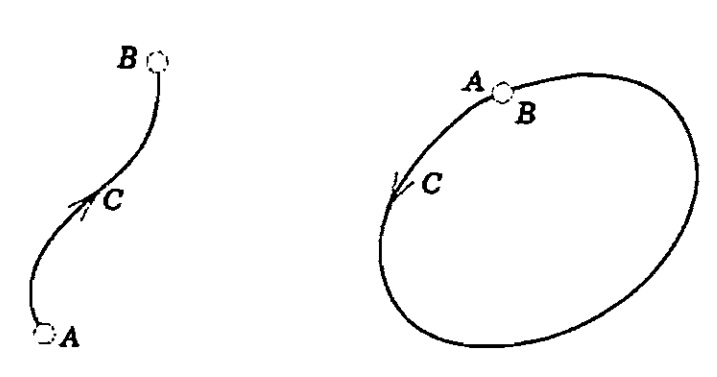
Se uma curva simples C é suave por partes, podemos orientá-la orientando cada parte suave de C como mostram as figuras abaixo:

Dada uma curva orientada C, representada por f(t)=(x(t), y(t),z(t)); t \in [a,b] , então definimos a curva -C como a curva C, mas com a orientação oposta. Nesse sentido, a curva -C é dada por $$ f^{-} (t) = f(a+b -t)=(x(a+b -t), y(a+b -t),z(a+b -t)); t \in [a,b].$$

EXEMPLO

Vamos parametrizar a circunferência de centro na origem e raio a no sentido horário.

Observe que no sentido horário a circunferência tem uma orientação oposta àquela que segue o crescimento de t \in [0, 2 \pi] .

Ou seja, queremos parametrizar -C, onde C é a circunferência.

Assim, como C: f(t)=(acos(t), a sen(t)); t \in [0, 2 \pi] , então $$-C: f^{-} (t) = f(0 + 2 \pi -t) = f(-t+2 \pi) = (acos(-t+2 \pi), a sen(-t+2 \pi)); t \in [0, 2 \pi]$$

Observando que as funções cosseno e seno são 2 \pi -periódicas e funções par e ímpar, respectivamente, ficamos com $$-C: f^{-} (t) = (acos(t), -a sen(t)); t \in [0, 2 \pi]$$

A imagem abaixo ilustra o exemplo:

Curva Regular

Para uma curva parametrizada \vec{f} (t) , ela é suave, ou regular, se tiver derivadas contínuas em todos os pontos do seus domínio e se \vec{f'} (t) \neq \vec{0} , \;\;\; \forall t \in I \subset \mathbb{R}.

Geometricamente uma curva suave é caracterizada pela ausência de pontos angulosos. Isso porque em cada um de seus pontos, a curva suave tem uma tangente única que varia continuamente quando se move sobre curva.

Por exemplo, as retas, circunferências, elipses e hélices são curvas suaves, enquanto triângulos, quadrados e ciclóides não são curvas suaves, mas sim suaves por partes.

Uma curva é suave por partes se puder ser dividida em um número finito de curvas suaves.

Considere uma curva C definida no espaço e o orientada pela escolha de um dos sentidos percorrendo C como direção positiva.

Defina A como o ponto inicial e B como o ponto onde que a curva termina.

Podemos representar C por uma representação paramétrica dada por $$r(s) = x(s)i + y(s)j + z(s) k$$ onde s é o comprimento de arco de C e A e B correspondem a s=a e s=b, respectivamente.

Arco Simples

Dizemos que um arco é simples quando cada um de seus pontos provém de um único valor t, isto é, se $$ t_1 \neq t_2 \Rightarrow \vec{f} (t_1) \neq \vec{f} (t_2).$$

Não sendo simples, o arco conterá ao meno um ponto múltiplo, assim designado todo pponto proveniente de dois ou mais valores do parâmetro t

Nesse sentido, diz-se que o arco é fechado quando suas extremidades coincidem e um arco fechado é simples quando todos os seus pontos são simples, à exceção de suas extremidades.

INTEGRAL DE LINHA DE PRIMEIRA ESPÉCIE

Nosso intuito é calcular a integral de uma função f(x,y,z) ao longo da curva C de A até B.

Esta integral sera denotada por $$\int\limits_{C}{f(x,y,z)}ds$$ onde s é o comprimento de arco da curva C que é denominada caminho de integração.

Imediatamente temos que

\begin{eqnarray*}
\int\limits_{C}{f(x,y,z)}ds & = & \int\limits_{a}^{b}{f(x(s),y(s),z(s))}ds\\
& = & \int\limits_{t_1}^{t_2}{f(x(t),y(t),z(t))}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2+ \left(\dfrac{dz}{dt}\right)^2}dt\\
\end{eqnarray*}

Esta integral é denominada integral de linha de primeira espécie de f sobre C.

Observe que para definir a integral de linha acima não é necessário que a função f esteja definida em ponto fora de C. Em particular, se \lambda =  \lambda (s) for uma função contínua do arco s , podemos definir sua integral sobre  C.

EXEMPLO

Calcule $$\int\limits_{C}{xy^3}ds$$ onde C é o segmento de linha y=2x no plano xy que tem extremos iguais a A(-1,-2,0) e B(1,2,0).

Primeiramente, parametrizando a curva C temos que x(t) = t e y(t) = 2t, ou seja $$r(t) = t i + 2t j\;\;\;\;\;\;\;\;\;\;\;\;\;-1 \leq t \leq 1.$$ Assim,

\begin{eqnarray*}
\int\limits_{C}{xy^3}ds & = & \int\limits_{-1}^{1}{t(2t)^3}\sqrt{1+2^2}dt\\
& = & \sqrt{5}\int\limits_{-1}^{1}{8t^4}dt\\
& = & \dfrac{16}{\sqrt{5}}
\end{eqnarray*}

EXEMPLO

Agora, vamos calcular a integral $$\int\limits_{C}{x^{-1}(y+z)}ds$$ onde C é o arco de círculo x^2 + y^2=4 no plano xy de extremos iguais a A(2,0,0) e B(\sqrt{2},\sqrt{2},0).

Temos que, a curva C é parametrizada por $$\left( x(t), y(t), z(t) \right) = \left( 2 \cos{t}, 2\sin{t},0 \right) = 2\cos{t} i + 2 \sin{t} j +0 k$$ onde t varia de 0 a \dfrac{\pi}{4} para que os extremos A(2,0,0) e B(\sqrt{2},\sqrt{2},0) sejam atingidos.

Sendo assim,
$$\int\limits_{C}{x^{-1}(y+z)}ds = $$ $$= \int\limits_{0}^{\frac{\pi}{4}}{(2\cos{t})^{-1} \sin{t}}\sqrt{4\cos^2{t}+4\sin^2{t}}dt =$$ $$ = 2\int\limits_{0}^{\frac{\pi}{4}}{\tan{t}}dt = $$ $$ = -2\ln{(\cos{t})}\left|_{0}^{\pi/4} \right.=  \ln{2}$$

PROPRIEDADES:

As propriedades das integrais de linha são análogas às propriedades das integrais indefinidas. Sendo C uma curva suave ou suave por partes e f e g duas funções contínuas em cada ponto de C, além das duas propriedades básicas de linearidade, podemos garantir que:

1) Se C é uma curva com ponto inicial A e um ponto terminal B; P um ponto de C entre A e B; C_1 a parte de C entre A e P e C_2 a parte de C de P até B, então $$ \int\limits_{C}{fds} = \int\limits_{C_1}{fds} + \int\limits_{C_2}{fds} .$$

2) \int\limits_{C}{fds} = \int\limits_{-C}{fds} , onde -C representa a curva C orientada no sentido oposto.

INTEGRAL DE LINHA DE SEGUNDA ESPÉCIE

Vamos considerar agora L=L(x,y,z), M=M(x,y,z) e N=N(x,y,z) funções definidas e contínuas numa região R de espaço de modo que $$\vec{F}(x,y,z) = L(x,y,z)i+M(x,y,z)j+N(x,y,z)k$$ seja um campo vetorial definido no aberto R e seja C um arco regular, todo contido em R com representação paramétrica $$P(t) = x(t) i + y(t) j +z(t) k\;\;\;\;a\leq t \leq b$$ que descreve um movimento em R.

Vamos definir a integral de linha de \vec{F}, ao longo do arco C, como sendo $$\int\limits_{C}{Ldx+Mdy+Ndz} = \int\limits_{C}{\vec{F}(P(t)).dP} $$ onde F(P) = (L(P(t)),M(P(t)), N(P(t))) e dP = (x'(t)dt, y'(t)dt, z'(t)dt) = P'(t)dt.

Esta integral é denominada de integral de linha de segunda espécie e sua forma clássica é dada por $$\int\limits_{a}^{b}{[Lx’+My’+Nz’]dt}$$

EXEMPLO

Calcule a integral da forma diferencial $$ydx-xdy+zdz$$ ao longo do arco de hélice $$C:x=\cos{t}, y=\sin{t}, z=t;\;\;\;\;\;0\leq t \leq \frac{\pi}{2}.$$

\begin{eqnarray*}
\int\limits_{C}{Ldx+Mdy+Ndz} & = & \int\limits_{0}^{\frac{\pi}{2}}{Lx’+My’+Nz’}dt\\
& = & \int\limits_{0}^{\frac{\pi}{2}}{-\sin^2{t}+\cos^2{t}+t}dt\\
& = & \int\limits_{0}^{\frac{\pi}{2}}{t-1}dt\\
& = & \dfrac{\pi^2 -4\pi}{8}
\end{eqnarray*}

EXEMPLO

Calcule a integral da forma diferencial $$xydx+y^2dy$$ ao longo dos arcos $$C_1:y=x^2;\;\;\;\;\;0\leq x \leq 1.$$ $$C_2:x=y^2;\;\;\;\;\;0\leq y \leq 1.$$
Temos que $$C_1:x=t, y=t^2;\;\;\;\;C_2:x=t^2, y=t;\;\;\;\;\;0\leq t \leq 1.$$

\begin{eqnarray*}
\int\limits_{C_1}{xydx+y^2dy} & = & \int\limits_{0}^{1}{t^3+2t^5}dt\\
& = & \dfrac{7}{12}
\end{eqnarray*}

\begin{eqnarray*}
\int\limits_{C_2}{xydx+y^2dy} & = & \int\limits_{0}^{1}{2t^4+t^2}dt\\
& = & \dfrac{11}{15}
\end{eqnarray*}

Podemos concluir que, em geral, a integral de dada forma diferencial depende do arco sobre o qual ela se processa, mesmo que se mude o arco e mantenha fixas suas extremidades.

Quando a integração se processa sobre um arco fechado C, é costume indicá-lo com a notação $$\oint\limits_{C}{F(P).dP}$$

EXEMPLO
Considere o campo vetorial \vec{F}(x,y)=(2x,y). Calcule $$\oint\limits_{C}{F(P).dP},$$ onde C é o círculo de raio 1 e centro na origem.

A parametrização da curva C é dada por $$P(t) = (\cos{t}, \sin{t})$$. Assim,

\begin{eqnarray*}
\oint\limits_{C}{F(P).dP} & = & \oint\limits_{C}{(2x,y).(dx,dy)}\\
& = & \oint\limits_{C}{(2xdx+ydy)}\\
& = & \int\limits_{0}^{2 \pi}{(-2\cos{t} \sin{t} + \cos{t} \sin{t})dt}\\
& = & \int\limits_{0}^{2 \pi}{-\cos{t} \sin{t}dt}\\
& = & 0.
\end{eqnarray*}

Integrais Curvilíneas Independentes do Caminho de Integração

Seja \vec{f} um campo vetorial em um domínio D do espaço. A Integral $$ \int\limits_{C}{\vec{f} \cdot d \vec{r}} $$ é dita independente do caminho de integração em D se, para qualquer par de pontos A e B.

TEOREMA

Se \vec{f} = \left( f_1 , f_2, f_3 \right) é um campo vetorial em um domínio conexo U \subset \mathbb{R}^3 , são equivalentes as três afirmações seguintes:

1) \vec{f} é um campo conservativo em U \subset \mathbb{R}^3 ;

2) A integral de linha de \vec{f} é independente do caminho de integração em U \subset \mathbb{R}^3 ;

3) A integral de linha de \vec{f} ao redor de todo caminho fechado em U \subset \mathbb{R}^3 é igual a zero.

OBSERVAÇÃO:

Pode-se ainda mostrar que se u = u \left( x , y, z \right) é uma função diferenciável em um domínio conexo U \subset \mathbb{R}^3 , tal que que \vec{f} = \nabla u é contínuo em U , então $$ \int\limits_{C}{\vec{f} \cdot d \vec{r}} = u(B) – u(A)$$ para qualquer caminho C em U , unindo o ponto A ao ponto B.

Teorema de Green no Plano

Integrais duplas sobre uma região plana podem ser transformadas em integrais de linha sobre uma região limitada a vice-versa.

Esta transformação na prática possui mais interesse teórico e pode ser feita como estipulado no teorema que segue.

Teorema de Green no Plano

Seja R uma região fechada e limitada no plano xy cuja fronteira consiste de uma quantidade finita de curvas regulares. Sejam f(x,y) e g(x,y) funções contínuas e cujas derivadas parciais \dfrac{\partial f}{\partial y} e \dfrac{\partial g}{\partial x} também são contínuas em algum domínio R. Então: $$\int\limits_{R} \int \left( \dfrac{\partial g}{\partial x} – \dfrac{\partial f}{\partial y} \right) dx dy= \int\limits_{C}\left( fdx +gdy \right).$$

EXEMPLO

Considere o campo vetorial \vec{F}(x,y) = (y+x^2\cos{x}, 2x-y^2\sin{y}).

Vamos utilizar o Teorema de Green no plano para calcular $$\oint\limits_{C}{F(P).dP}$$ onde C é a circunferência com centro em (0,0) e raio igual a 1:

\begin{eqnarray*}
\oint\limits_{C}{F(P).dP} & = & \int\limits_{R} \int \left( 2 – 1\right) dx dy\\
& = & \int\limits_{0}^{2\pi} \int\limits_{0}^{1}r dr d\theta\\
& = & \pi
\end{eqnarray*}

Observe que se fossemos efetuar o cálculo desta integral de linha como usualmente fazemos teriamos que solucionar a integral
$$\int\limits_{0}^{2\pi}{\left[ -(\sin{t} + \cos^2{t}\cos{(\cos{t})})\sin{t} +(2\cos{t}-\sin^2{t}\sin{(\sin{t})})\cos{t} \right]}dt$$

Listas de Exercícios Resolvidos:

• Integral de Linha de 1ª Espécie | 1ª Lista de Exercícios Resolvidos
• Integral de Linha de Campos Vetoriais | 1ª Lista de Exercícios Resolvidos
• O Teorema de Green No Plano | 1ª Lista de Exercícios Resolvidos

Leia Mais:

• Integral de Superfície | Campos Escalares, Campos Vetoriais e Fluxos
• Integral de Superfície | Teoremas de Stokes e da Divergência
• Integral Dupla | Teorema de Fubini, Exemplos e Exercícios Resolvidos
• Integral de Fourier | Fator Descontínuo de Dirichlet e Integrais de Laplace

Assista nossa Vídeo-Aula  Sobre Integrais de Linha