Integral de Linha de 1ª Espécie | 1ª Lista de Exercícios Resolvidos

As Integrais de Linha e de superfície são outras formas importantes de se estender a noção de integral. Em geral, integrais deste tipo aparecem quando consideramos distribuições lineares de massa ou carga elétrica e o trabalho de uma força, por exemplo.

Para calcular a integral de uma função f(x,y,z) ao longo da curva C de A até B. Esta integral sera denotada por $$\int\limits_{C}{f(x,y,z)}ds$$ onde s é o comprimento de arco da curva C que é denominada caminho de integração.

Imediatamente temos que

\begin{eqnarray*}
\int\limits_{C}{f(x,y,z)}ds & = & \int\limits_{a}^{b}{f(x(s),y(s),z(s))}ds\\
& = & \int\limits_{t_1}^{t_2}{f(x(t),y(t),z(t))}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2+ \left(\dfrac{dz}{dt}\right)^2}dt\\
\end{eqnarray*}

Donde podemos garantir que:

1) Se C é uma curva com ponto inicial A e um ponto terminal B; P um ponto de C entre A e B; C_1 a parte de C entre A e P e C_2 a parte de C de P até B, então $$ \int\limits_{C}{fds} = \int\limits_{C_1}{fds} + \int\limits_{C_2}{fds} .$$

2) \int\limits_{C}{fds} = \int\limits_{-C}{fds} , onde -C representa a curva C orientada no sentido oposto.

Integral de Linha | 1ª Lista de Exercícios Resolvidos

1. Calcule \int\limits_{C}{(x^2+y^2+z^2)ds} onde C é a hélice $$\gamma (t) = (2cos(t) , 2 sen(t), 5t), \;\;\;t \in [0, 2 \pi].$$

SOLUÇÃO: $$\int\limits_{C}{(x^2+y^2+z^2)ds} = \int\limits_{0}^{2 \pi}{\left( 4 cos^2(t) + 4 sen^2 (t) + 25 t^2 \right) \sqrt{(-2sen(t))^2 + (2cos(t))^2 + 25}dt}= $$ $$=  \int\limits_{0}^{2 \pi}{(4 + 25 t^2) \sqrt{29} dt} = \sqrt{29} \left( 8 \pi + \frac{200}{3} \pi ^3 \right).$$

2. Se C é a curva que contorna uma região plana R dada nas condições do Teorema de Green, podemos calcular a área de figuras planas usando a fórmula $$A_R = \frac{1}{2}\oint_{C}{(xdy – ydx)}.$$ Usando essa fórmula, estabeleça uma fórmula para área delimitada pela elipse $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$$

SOLUÇÃO: Como a elipse pode ser parametrizada como $$ \gamma (t) = \left( a cos(t), b sen(t) \right), $$ então $$A_R = \frac{1}{2}\oint_{C}{(xdy – ydx)} = \frac{1}{2} \int\limits_{0}^{2 \pi}{(a cost b cost + b sent a sent) dt} = \frac{1}{2} \int\limits_{0}^{2 \pi}{ab dt} = ab \pi u. a.$$

3) \int\limits_{C}{x^{-1}(y+z)}ds onde C é o arco de círculo x^2 + y^2=4 no plano xy de extremos iguais a A(2,0,0) e B(\sqrt{2},\sqrt{2},0).

SOLUÇÃO: Temos que, a curva C é parametrizada por $$\left( x(t), y(t), z(t) \right) = \left( 2 \cos{t}, 2\sin{t},0 \right) = 2\cos{t} i + 2 \sin{t} j +0 k$$ onde t varia de 0 a \dfrac{\pi}{4} para que os extremos A(2,0,0) e B(\sqrt{2},\sqrt{2},0) sejam atingidos.

Sendo assim,
$$\int\limits_{C}{x^{-1}(y+z)}ds = $$ $$= \int\limits_{0}^{\frac{\pi}{4}}{(2\cos{t})^{-1} \sin{t}}\sqrt{4\cos^2{t}+4\sin^2{t}}dt =$$ $$ = 2\int\limits_{0}^{\frac{\pi}{4}}{\tan{t}}dt = $$ $$ = -2\ln{(\cos{t})}\left|_{0}^{\pi/4} \right.=  \ln{2}$$

4) \int\limits_{C}{x}ds onde C é o contorno fechado OAB formado pela parábola x = 0 , y = 1 e a parábola y = x^2, x \geq 0 .

SOLUÇÃO: Observe que neste caso temos uma curva suave por partes.

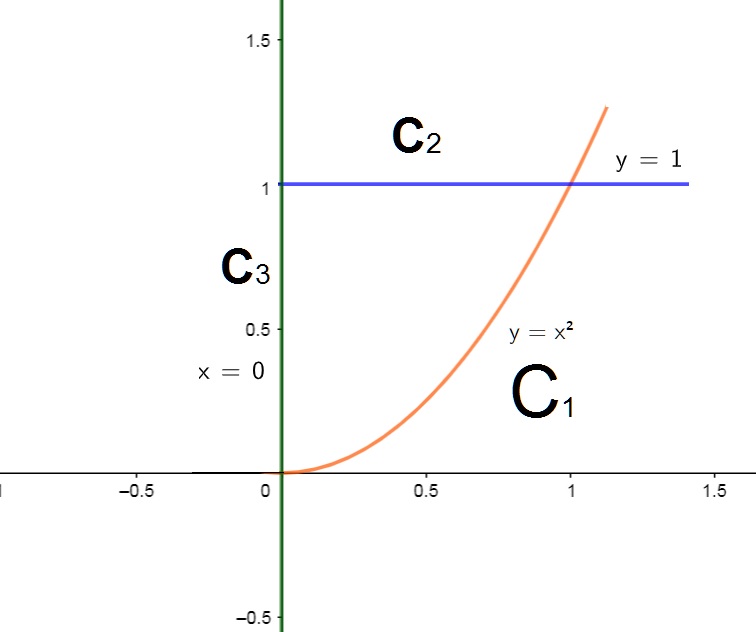
Desta forma orientaremos a curva C, passando por três curvas suaves dadas por:

• C_1 : a parcela da parábola y = x^2 que vai do ponto (0,0) na direção do ponto (1,1), que tem equações paramétricas dadas por $$x(t) = t, \qquad y(t) = t^2; \qquad 0 \leq t \leq 1;$$
• C_2 : a parcela da reta y = 1 que vai do ponto (1,1) ao ponto (0,1), que tem equações paramétricas dadas por $$x(t) = 1-t \qquad y(t) = 1; \qquad 0 \leq t \leq 1;$$
• C_3 : a parcela da reta x = 0 que vai do ponto (0,1) ao ponto (0,0), que tem equações paramétricas dadas por $$x(t) = 0, \qquad y(t) = 1-t; \qquad 0 \leq t \leq 1.$$

Logo, $$ \int\limits_{C}{x}ds = \int\limits_{C_1}{x}ds + \int\limits_{C_2}{x}ds + \int\limits_{C_3}{x}ds = $$ $$ = \int\limits_{0}^{1}{x}ds + \int\limits_{0}^{1}{x}ds + \int\limits_{0}^{1}{x}ds = \int\limits_{0}^{1}{t \sqrt{1+4t^2}}dt + \int\limits_{0}^{1}(1-t) \sqrt{2}dt + \int\limits_{0}^{1}{0}dt  = $$ $$ = \frac{\sqrt{125} – 1}{12} + \frac{\sqrt{2}}{2}$$

5) Calcule $$\int_{C}{xyds}$$ onde C é o arco dado por $$C: \qquad x = cos(t), y= sen(t), z = t; \qquad 0 \leq t \leq \pi/2 .$$

SOLUÇÃO: $$\int_{C}{xyds} = \int_{0}^{\pi /2}{cos(t)sen(t) \sqrt{2} dt} = \sqrt{2} \int_{0}^{\pi /2}{cos(t)sen(t)dt} = \frac{\sqrt{2}}{2} .$$

6) Calcule $$\int\limits_{C} ysen(z)ds$$ onde C é hélice circular dada pelas equações paramétricas $$x = cos(t); \qquad y = sen(t); \qquad z = t; \qquad 0 \leq t \leq 2 \pi .$$

SOLUÇÃO: A fórmula de cálculo da integral de linha nos mostra que $$ \int\limits_{C} ysen(z)ds = \int\limits_{0}^{2 \pi}{[sen(t)]sen(t) \sqrt{sen^2 (t) + cos^2 (t) +1}dt} = \\ = \sqrt{2} \int\limits_{0}^{2 \pi}{\frac{1}{2} [1-cos(2t)] dt} = \frac{\sqrt{2}}{2} \left[ t – \frac{1}{2} sen(2t) \right]_{0}^{2 \pi} = \sqrt{2} \pi .$$

Leia Mais:

• Integral de Linha de Campos Vetoriais | 1ª Lista de Exercícios Resolvidos
• Integral de Linha de 1ª e 2ª Espécies, e o Teorema de Green no Plano
• Integral de Superfície | Campos Escalares, Campos Vetoriais e Fluxos
• Integral de Superfície | Teoremas de Stokes e da Divergência

Assista nossa Vídeo-Aula  Sobre Integrais de Linha