A Equação de Bessel é uma E.D.O. de 2ª Ordem que aparece em estudos avançados de matemática aplicada na física e na engenharia. Neste artigo solucionamos esta equação.
A equação diferencial $$x^2 y” + x y’ + (x^2 -v^2) y = 0 , \tag{1} $$ onde v é uma constante dada, é conhecida como equação de Bessel e é uma das mais importantes equações da matemática aplicada. Para estudá-la, assumimos que v é um número não negativo.
Friedrich Wilhelm Bessel (1784 – 1846) foi uma astrônomo e matemático alemão que em 1838 mediu, pela primeira vez a distância da estrela 61 Cygni. Em 1840 ele previu a existência de uma massa planetária além da órbita de Urano e o planeta Netuno seria descoberto seis anos depois. A equação (1) aparece em seu trabalho sobre movimento planetário, mas ela e sua solução foram provavelmente descobertas por Daniel Bernoulli em sua pesquisa sobre determinação dos deslocamentos de uma corrente oscilatória.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
A Solução da Equação de Bessel
Para resolver a equação de Bessel lançaremos mão do teorema abaixo, enunciado no artigo anterior, sobre soluções de EDO’s por séries em torno de pontos singulares e o método de Frobenius:
TEOREMA 1: Qualquer equação diferencial na forma $$ y” + \frac{a(x)}{x} y’ + \frac{b(x)}{x^2} y = 0 \tag{2} $$ onde as funções a(x) e b(x) são analíticas em x = 0 , tem ai menos uma solução a qual podem ser representadas na forma $$ y(x) = \sum_{m=0}^{\infty}{c_m x ^m} = x^r \left( c_0 + c_1 x + c_2 x^2 + …. \right), \qquad c_0 \neq 0\label{3} $$ onde o expoente r pode ser qualquer número real ou complexo.
A equação de Bessel está na forma canônica deste teorema, logo possui uma solução na forma (3). Substituindo esta expressão e suas derivadas de primeira e segunda ordens na equação de Bessel, imediatamente obtemos $$ \sum_{m=0}^{\infty}{(m + r) (m + r-1) c_m x^{m + r } } + \sum_{m=0}^{\infty}{(m + r) c_m x^{m + r } } + \\ + \sum_{m=0}^{\infty}{ c_m x^{m + r+2} } – v^2 \sum_{m=0}^{\infty}{ c_m x^{m + r} }= 0.$$
Igualando a soma dois coeficientes encontramos $$ (a) \qquad r(r-1)c_0 + r c_0 – v^2 c_0 = 0 \qquad (s=0) \\ (b) \qquad (r+1)rc_1 + (r+1)c_1 – v^2 c_1 = 0 \qquad (s=1) \\ (c) \qquad (s+r)(s+r-1)c_s + (s+r)c_s +c_{s-2} – v^2 c_s = 0 \qquad (s=2,3,… ) \tag{3}$$ De (3a) obtemos a função indicial $$(r+v)(r-v) = 0 \tag{4}$$ cujas raízes são r_1 = v (\geq 0) e r_2 =-v .
Primeiramente vamos determinar uma solução correspondente à raiz r_1 . Para este valor de r , a equação (3b) leva a c_1 = 0 e a equação (3c) pode ser escrita como $$ (s+r+v)(s+r-v)c_s +c_{s-2} = 0, $$ e como r = v isso nos leva a $$(s+2v)sc_s + c_{s-2} = 0 \tag{5} $$ Desde que c_1 = 0 e v \geq 0 , daí segue que c_3 = c_5 = c_7 = ... = 0 . Se colocarmos s= 2m em (5), obteremos $$c_{2m} = – \frac{1}{2^2 m(v+m)} c_{2m-2} = \frac{(-1)^m c_0}{2^{2m} m! (1+v)(2+v)…(m+v)} \qquad m =1,2,3,… \tag{6} $$ e assim poderemos determinar os coeficientes c_2 , c_4 , ... partindo de c_0 .
Sendo c_0 arbitrário, é comum definir $$c_0 = \frac{1}{2^v \Gamma (v+1)} $$ onde \Gamma (v+1) é a função gama (veja nosso artigo sobre a função gama.) Como esta função possui a conveniente propriedade $$ \Gamma(1 + \alpha ) = \alpha \Gamma ( \alpha ),$$ podemos reduzir o produto indicado no denominador de (6) a um termo. Por exemplo, \begin{eqnarray} \Gamma (1+v+1) & = & (1+v) \Gamma (1 + v)\\ \Gamma (1+v+2) & = & (2+v) \Gamma (2 + v)\\ & = & (2+v) (1+v) \Gamma (1 + v) \end{eqnarray}
Com isso, podemos escrever (6) como $$c_{2m} = \frac{(-1)^m c_0}{2^{2m} m! (1+v)(2+v)…(m+v)} = \\ \frac{(-1)^m }{2^{2m+v} m! (1+v)(2+v)…(m+v) \Gamma (1+v)} = \frac{(-1)^m }{2^{2m+v} m! \Gamma (1+v+m)} \qquad m =0,1,2,3,…$$ Seque-se que a solução é $$ y(x) = \sum\limits_{m=0}^{\infty}{c_{2m} x^{2m+v}} = \sum\limits_{m=0}^{\infty}{\frac{(-1)^m }{ m! \Gamma (1+v+m)} \left( \frac{x}{2} \right)^{2m+v}}$$ e se v \geq 0 , a série converge pelo menos no intervalo [0, \infty) , e esta é uma solução particular da equação de Bessel a qual é denotada por $$ J_v (x) = \sum\limits_{m=0}^{\infty}{\frac{(-1)^m }{ m! \Gamma (1+v+m)} \left( \frac{x}{2} \right)^{2m+v}}$$
Funções de Bessel de Primeira Espécie
A solução serial $$ J_v (x) = \sum\limits_{m=0}^{\infty}{\frac{(-1)^m }{ m! \Gamma (1+v+m)} \left( \frac{x}{2} \right)^{2m+v}} \tag{7} $$ é conhecida como função de Bessel de primeira espécie de ordem v . Ainda para o seguinte expoente r_2 = - v , obtemos, exatamente da mesma maneira, $$ J_{-v} (x) = \sum\limits_{m=0}^{\infty}{\frac{(-1)^m }{ m! \Gamma (1-v+m)} \left( \frac{x}{2} \right)^{2m-v}}$$ que é a função de Bessel de primeira espécie de ordem -v .
Valores inteiros de v são frequentemente denotados por n . Desta forma, para n \geq 0 , obtemos $$ J_n (x) = \sum\limits_{m=0}^{\infty}{\frac{(-1)^m }{ m! \Gamma (1+n+m)} \left( \frac{x}{2} \right)^{2m+n}} = \sum\limits_{m=0}^{\infty}{\frac{(-1)^m }{ m! (n+m)!} \left( \frac{x}{2} \right)^{2m+n}}.$$
Por exemplo, a função de Bessel de primeira espécie de ordem zero é $$ J_0 (x) = 1 – \frac{x^2}{2^2 (1!)^2} + \frac{x^4}{2^4 (2!)^2} – \frac{x^6}{2^6 (3!)^2}+…,$$ e a função de Bessel de primeira ordem é $$ J_1 (x) = \frac{x}{2} – \frac{x^3}{2^3 (1!)2!} + \frac{x^5}{2^5 (2!)3!} – \frac{x^7}{2^7 (3!)4!}+… \; .$$ Ambas estão ilustradas no gráfico abaixo.
Funções de Bessel de primeira ordem J0 e J1.
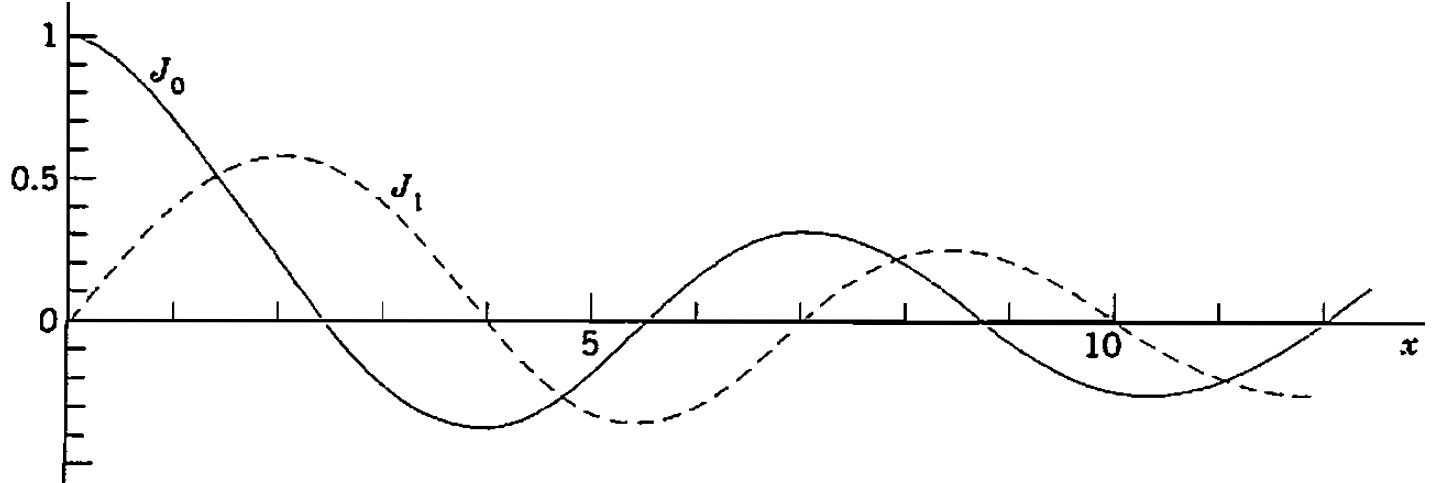
É interessante notar que para v = \dfrac{1}{2} a série em (7) se torna a conhecida expansão de McLaurin. Usando a relação \Gamma (1/2) = \sqrt{ \pi} (que foi mostrado neste artigo sobre a função Gama.) Assim, podemos calcular ainda $$ J_{1/2} (x) = \sqrt{\frac{2}{\pi x} } \text{sen}(x).$$
Como a equação de Bessel envolve v^2 , as funções J_v e J_{-v} são soluções da equação para o mesmo v . Elas são linearmente independentes, porque o primeiro termo das duas são finitos múltiplos de x^v e x^{-v} diferentes de zero. Desta forma, quando v não é um inteiro, a solução geral da equação de Bessel para todo x \neq 0 é $$ y(x) = a_1 J_v (x) + a_2 J_{-v} (x) .$$
Funções de Bessel de 2ª Espécie
Para valores não-inteiros de v , as funções de Bessel J_n e J_{-n} são linearmente dependentes e não formam um conjunto fundamental de soluções. Assim, se v não é inteiro, a função definida pela combinação linear $$ Y_{v}(x) = \frac{\text{cos} (v \pi) J_v (x) – J_{-v} (x)}{\text{sen} ( v \pi ) } \tag{8} $$ e a função J_v são soluções linearmente independentes de (1).
Logo, uma outra forma para a solução geral de (1) é $$y(x) = c_1 J_v (x) + c_2 Y_v (x),$$ desde que v \neq \text{inteiro} . Quando v \rightarrow m \in \mathbb{Z} , então (8) possui a forma indeterminada 0/0. Porém, pode ser mostrado pela regra de L’Hôpital, que $$ \lim\limits_{v \rightarrow m}{Y_{v}(x) } $$ existe. Ainda, a função $$ Ym (x) = \lim\limits_{v \rightarrow m}{Y_{v}(x) } $$ e J_m (x) são soluções linearmente independentes de $$x^2 y” + xy’+(x^2 -m^2) y = 0.$$
Portanto, para qualquer valor de v , a solução geral para (1) em (0, \infty ) pode ser escrita como $$y = c_1 J_v (x) + c_2 Y_v (x).$$ Y_v (x) é algumas vezes chamada de função de Neumann, também denotada por N_v(x) , mais comumente, Y_v (x) é chamada de função de Bessel de segunda espécie de ordem v .
Devemos ainda mencionar que existe uma necessidade prática por soluções da equação de Bessel que são complexas para valores reais de x . Por esta razão as soluções \begin{eqnarray} H^{1}_{v} (x) & = & J_v (x) + i Y_v (x) \\ H^{2}_{v} (x) & = & J_v (x) – i Y_v (x) \end{eqnarray} são frequentemente usadas e tabelas. Estas funções linearmente independentes são denominadas funções de Bessel de terceira espécie de ordem v ou primeira e segunda função de Henkel de ordem v .
Funções de Bessel de segunda espécie Y0 e Y1
EXEMPLO: A solução geral para a equação $$ x^2 y” + x y’ + (x^2 -9) y = 0 $$ em (0, \infty ) , observando que v = 3 , é dada que $$ y(x) = c_1 J_3 (x) + c_2 Y_3 (x) .$$
A Equação de Bessel Paramétrica
Trocando x por \lambda x em (1) e usando a regra de cadeia, obtemos uma forma alternativa da equação de Bessel conhecida como equação de Bessel paramétrica: $$ x^2 y” + x y’ + \left( \lambda ^2 x^2 – v^2 \right) y = 0 . \tag{12} $$ A solução geral para (12) é $$ y(x) = c_1 J_{v} ( \lambda x ) + c_2 Y_{v} ( \lambda x ) .$$
Tabelas de Valores das Funções de Bessel
Valores funcionais de J_0 (x) e J_1 (x) para alguns valores selecionados de x são dados na tabela abaixo. Os zeros dessas duas funções, a saber, os valores de x para os quais J_0 (x) = 0 e J_1 (x) = 0 , são importantes em algumas aplicações de equações diferenciais parciais.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
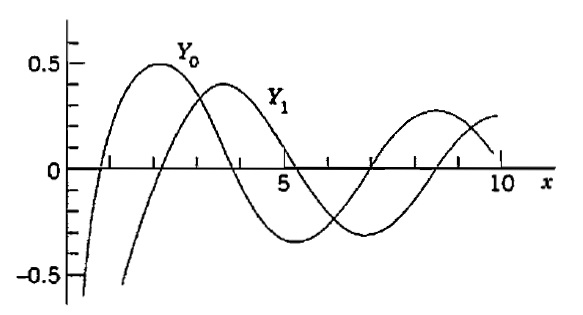
Abaixo temos uma tabela com os valores de Y_0 (x) e Y_1 (x)
Propriedades das Funções de Bessel
Para trabalhar com as funções de Bessel é necessário saber que estas funções satisfazem várias relações e propriedades. Listamos abaixo algumas propriedades úteis das funções de Bessel de ordem m = 0,1,2,3,... : \begin{eqnarray} (i) & & J_{-m} (x) = (-1)^m J_m (x) \\ & & \\ (ii) & & J_{m} (-x) = (-1)^m J_m (x) \\ & & \\ (iii) & & J_{m} (0) =0, m>0 \\ & & \\ (iv) & & J_{0} (0) = 1 \\ & & \\ (v) & & \lim_{x \rightarrow 0^+}{Y_{m} (x) } = – \infty \\ & & \\ (vi) & & \frac{d}{dx} \left[ x^v J_v (x) \right] = x^v J_{v-1} (x) \\ & & \\ (vii) & & \frac{d}{dx} \left[ x^{-v} J_{-v} (x) \right] = – x^{-v} J_{v+1} (x) \\ & & \\ (viii) & & J_{v-1}(x) + J_{v+1} (x) = \frac{2v}{x} J_v (x) \\ & & \\ (ix) & & J_{v-1}(x) – J_{v+1} (x) = 2J_v ‘ (x) \end{eqnarray}
Usando estas propriedades conseguimos resultados interessantes. Sabendo que $$ J_{1/2} (x) = \sqrt{\frac{2}{\pi x} } \text{sen}(x)$$ podemos concluir que $$ J_{-1/2} (x) = \sqrt{\frac{2}{\pi x} } \text{cos}(x).$$
Note que a propriedade (ii) indica que J_m (x) é uma função par se m for um inteiro par e uma função ímpar se m for um inteiro ímpar. Os gráficos de Y_0 (x) e Y_1 (x) serão dados abaixo e ilustram a propriedade (v): Y_m (x) é ilimitada na origem. Esse fato não é óbvio a partir de (8). Pode ser mostrado que, para x>0 , $$ Y_0 (x) = \frac{2}{ \pi} J_0 (x) \left[ \gamma + \ln{\frac{x}{2}} \right] – \frac{2}{ \pi} \sum_{k=1}^{\infty}{\frac{(-1)^k}{(k!)^2} \left( 1 + \frac{1}{2} + … + \frac{1}{k} \right) \left( \frac{x}{2} \right)^{2k} },$$ em que \gamma = 0,57721566... é a constante de Euler-Mascheroni. Observe que, por causa da presença do termo logarítmico, Y_0 (x) é descontínuo em x = 0 .
Já as fórmulas de recorrência (viii) e (ix) são de grande importância prática. Por exemplo, (viii) serve para expressar funções de Bessel de ordens mais altas em termos de funções de ordens mais baixas. Aplicando (viii) em $$ J_{1/2} (x) = \sqrt{\frac{2}{\pi x} } \text{sen}(x)$$ obtemos $$ J_{3/2} (Ix) = \frac{1}{x} J_{1/2}(x) – J_{-1/2} (x) = \sqrt{\frac{2}{\pi x} } \left( \frac{\text{sen}(x)}{x} – \text{cos}(x) \right)$$ $$ J_{-3/2} (Ix) = – \frac{1}{x} J_{-1/2}(x) – J_{1/2} (x) = – \sqrt{\frac{2}{\pi x} } \left( \frac{\text{cos}(x)}{x} – \text{sen}(x) \right)$$ e assim por diante, donde poderemos concluir que para v = \pm \frac{1}{2}, \pm \frac{3}{2}, \pm \frac{5}{2}, ... as funções de Bessel são funções elementares.
Leia Mais:
- Soluções de EDO’s por Séries em Torno de Pontos Singulares: O Método de Frobenius
- A Equação e os Polinômios de Legendre | Solução de E.D.O.’s Por Séries
- E.D.O.’s Por Séries de Potência | Solução em Torno de Pontos Ordinários
- E.D.O.’s e as Séries de Potências | 2ª Lista de Exercícios Resolvidos
