Transformada de Fourier | 2ª Lista de Exercícios Resolvidos

Neste artigo queremos apresentar uma segunda lista de exercícios resolvidos sobre a Transformada de Fourier, que é uma transformada integral que expressa uma função em termos de funções de base sinusoidal. Nela usamos a definição para calcular a transformada de Fourier de duas funções especiais que trazem a composição de exponenciais e trigonométricas com polinômios.

A Transformada de Fourier de uma função f(x) é definida pela integral $$\mathscr{F}\{ f(x) \} = \int\limits^{\infty}_{-\infty}{f(x)e^{-i\alpha x}dx} = F(\alpha)$$ e sua Transformada Inversa de Fourier é dada por $$\mathscr{F}^{-1}\{ F(\alpha) \} = \frac{1}{2\pi}\int\limits^{\infty}_{-\infty}{F(\alpha)e^{i\alpha x}d\alpha} = f(x).$$ As constantes 1 e \dfrac{1}{2 \pi} que precedem as integrais da definição da Transformada de Fourier poderiam ser substituídas por quaisquer outras constantes cujo produto fosse \dfrac{1}{2 \pi} .

Transformada de Fourier | 2ª Lista de Exercícios Resolvidos

1) Ache as transformadas de Fourier das seguintes funções:

a) f(x) = e^{- \lambda x^2} \text{cos} ( \beta x) com \lambda > 0 ;

SOLUÇÃO: Pela definição obtemos $$ F(\alpha) = \frac{1}{\sqrt{2\pi}} \int\limits^{\infty}_{-\infty}{f(x)e^{-i\alpha x}dx} = $$ $$ = \frac{1}{\sqrt{2\pi}} \int\limits^{\infty}_{-\infty}{e^{- \lambda x^2} \text{cos} ( \beta x)e^{-i\alpha x}dx} = $$ $$ = \frac{1}{\sqrt{2\pi}} \int\limits^{\infty}_{-\infty}{e^{- \lambda x^2 + i\alpha x} \text{cos} ( \beta x)dx}.$$

Usando a relação $$ \text{cos} ( \beta x) =  \frac{1}{2} \left( e^{i \beta x} + e^{- i \beta x} \right)$$ encontramos $$F( \alpha ) = \frac{1}{2\sqrt{2\pi}} \int\limits^{\infty}_{-\infty}{e^{- \lambda x^2 + i(\alpha + \beta) x}dx} + \\ + \frac{1}{2\sqrt{2\pi}} \int\limits^{\infty}_{-\infty}{e^{- \lambda x^2 + i(\alpha – \beta) x}dx}.$$

Completando os quadrados dos expoentes: $$ – \lambda x^2 + i \left( \alpha + \beta \right) x = – \left[ \lambda x^2 + 2 \frac{i ( \alpha + \beta) }{2 \sqrt{ \lambda} } x \sqrt{ \lambda} – \frac{( \alpha + \beta )^2}{4 \lambda} + \frac{( \alpha + \beta )^2}{4 \lambda} \right] = $$ $$ = – \left[ \sqrt{ \lambda} x +  \frac{i ( \alpha + \beta) }{2 \sqrt{ \lambda} } \right]^2 – \frac{( \alpha + \beta )^2}{4 \lambda} .$$

$$ – \lambda x^2 + i( \alpha – \beta ) x = – \left[ \lambda x^2 + 2 \frac{i ( \alpha – \beta )}{2 \sqrt{ \lambda }} x \lambda – \frac{( \alpha – \beta )^2 }{4 \lambda } + \frac{( \alpha – \beta )^2}{4 \lambda } \right]= $$ $$ = – \left[ \sqrt{ \lambda} x +  \frac{i ( \alpha – \beta) }{2 \sqrt{ \lambda} } \right]^2 – \frac{( \alpha + \beta )^2}{4 \lambda} .$$

Logo, $$ F ( \alpha ) = \frac{1}{ 2 \sqrt{ 2 \pi } } e^{- \frac{(\alpha + \beta)^2}{4 \lambda} } \int\limits^{\infty}_{-\infty}{e^{-\left[ \sqrt{ \lambda} x +  \frac{i ( \alpha + \beta) }{2 \sqrt{ \lambda} } \right]^2}dx} +$$ $$ + \frac{1}{ 2 \sqrt{ 2 \pi } } e^{- \frac{(\alpha – \beta)^2}{4 \lambda} } \int\limits^{\infty}_{-\infty}{e^{-\left[ \sqrt{ \lambda} x +  \frac{i ( \alpha – \beta) }{2 \sqrt{ \lambda} } \right]^2}dx}.$$

Vamos definir k_1 := \dfrac{\alpha + \beta}{2 \sqrt{ \lambda} } e k_2 := \dfrac{\alpha - \beta}{2 \sqrt{ \lambda} } e fazer as mudanças de variáveis $$ u = \sqrt{ \lambda } x + i k_1 \Leftrightarrow dx = \frac{du}{ \sqrt{\lambda}} $$  $$v = \sqrt{ \lambda } x + i k_2 \Leftrightarrow dx = \frac{dv}{ \sqrt{\lambda}} .$$

Então, $$ F( \alpha ) = \frac{1}{ 2 \sqrt{ 2 \pi \lambda} } e^{- \frac{(\alpha + \beta)^2}{4 \lambda} } \int\limits^{\infty + i k_1}_{-\infty + i k_1}{e^{-u^2}du} + \frac{1}{ 2 \sqrt{ 2 \pi \lambda} } e^{- \frac{(\alpha – \beta)^2}{4 \lambda} } \int\limits^{\infty + i k_2}_{-\infty+ i k_2}{e^{-v^2}dv}.$$

Para k \in \mathbb{R} , é fácil mostrar que $$ \int\limits^{\infty + i k}_{-\infty + i k}{e^{-y^2}dy} = \sqrt{ \pi } .$$ Então, encontramos $$ F( \alpha ) = \frac{1}{ 2 \sqrt{ 2 \lambda} } e^{- \frac{(\alpha + \beta)^2}{4 \lambda} }+ \frac{1}{ 2 \sqrt{ 2 \lambda} } e^{- \frac{(\alpha – \beta)^2}{4 \lambda} } .$$

b) f(x) = \dfrac{\text{cos} ( \beta x)}{a^4 + x^4}

SOLUÇÃO: Pela definição obtemos $$ F(\alpha) = \frac{1}{\sqrt{2\pi}} \int\limits^{\infty}_{-\infty}{f(x)e^{-i\alpha x}dx} = $$ $$ = \frac{1}{\sqrt{2\pi}} \int\limits^{\infty}_{-\infty}{\frac{ \text{cos} ( \beta x)e^{i\alpha x}}{a^4 + x^4} dx} = $$ $$ = \frac{1}{2 \sqrt{2\pi}} \int\limits^{\infty}_{-\infty}{\frac{ e^{i(\alpha + \beta ) x} + e^{i(\alpha – \beta ) x}}{a^4 + x^4} dx}.$$

Fazendo a substituição $$ x = |a| u \Leftrightarrow dx = |a| du $$ obtemos $$ F(\alpha) = \frac{|a|}{2 \sqrt{2\pi}} \int\limits^{\infty}_{-\infty}{\frac{ e^{i|a| (\alpha + \beta ) u} + e^{i|a| (\alpha – \beta ) u}}{a^4 \left( 1 + u^4 \right) } du} = $$ $$ = \frac{1}{2 |a|^3 \sqrt{2\pi}} \int\limits^{\infty}_{-\infty}{\frac{ e^{i|a| (\alpha + \beta ) u} + e^{i|a| (\alpha – \beta ) u}}{1 + u^4 } du}. $$

Observe que em ambos os casos temos que resolver $$  \int\limits^{\infty}_{-\infty}{\frac{e^{i \gamma u}}{1 + u^4} du }, $$ onde \gamma = |a| ( \alpha + \beta ) ou |a| ( \alpha - \beta ) .

Observe que $$ 1 + u^4 = 0 \Rightarrow u = (-1)^{1/4} \Rightarrow u = \left( e^{i \pi}   \right)^{1/4} \Rightarrow $$ $$ \Rightarrow u_k = \text{cos} \left( \frac{\pi + 2 \pi k}{4} \right) + i \text{sen} \left( \frac{\pi + 2 \pi k}{4} \right) \Rightarrow $$  $$ \Rightarrow u_k = e^{i \left( \frac{\pi + 2 \pi k}{4} \right)}; \qquad \text{ para } k = 0,1,2, 3 $$ Assim, $$ u_0 = e^{i \frac{\pi}{4} }, \qquad u_1 = e^{i \frac{\pi}{4}}, \qquad u_2 = e^{i \frac{5 \pi}{4}}, \qquad u_3 = e^{i \frac{7\pi}{4}} .$$

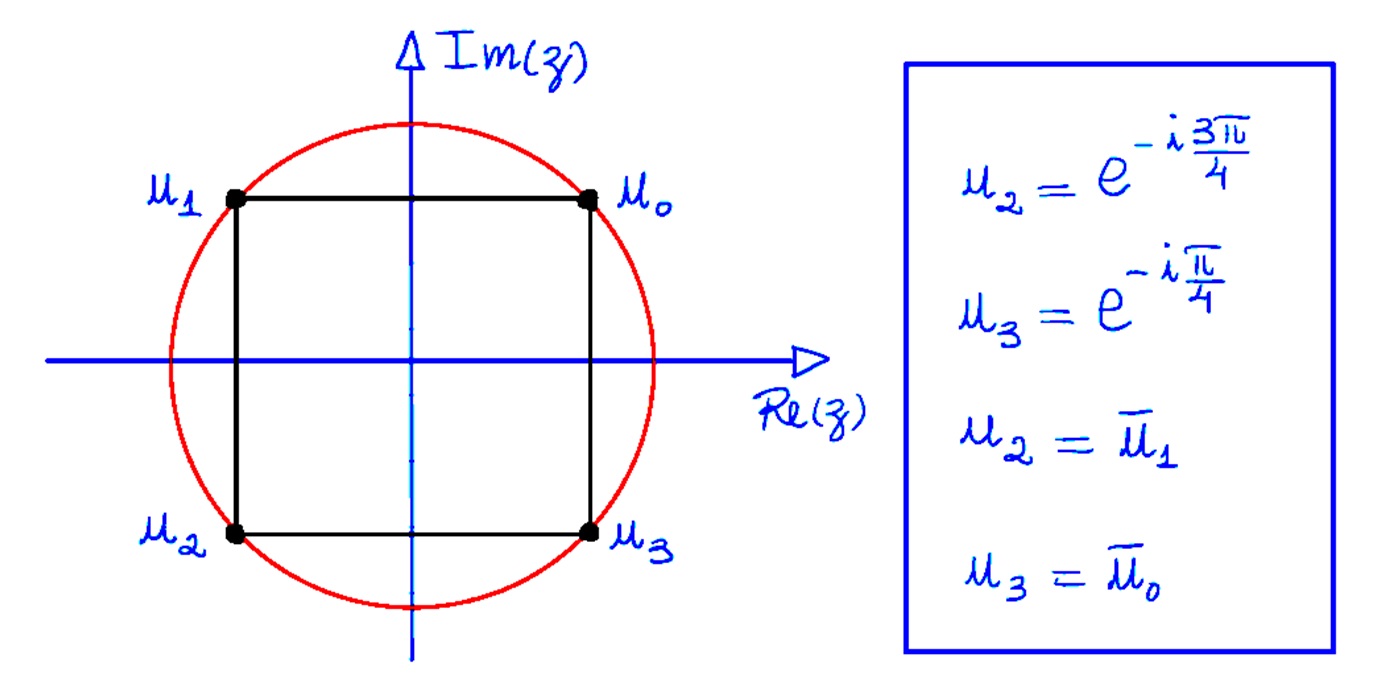
Observe que u_3 = \overline{u_0} e u_2 = \overline{u_1} .

Vamos agora aplicar o teorema do resíduo para resolver $$  \int\limits^{\infty}_{-\infty}{\frac{e^{i \gamma u}}{1 + u^4} du }. $$

Primeiramente consideramos \gamma > 0 temos $$  \oint\limits_{C}{\frac{e^{i \gamma z}}{1 + z^4} dz }. $$. Assim, fazendo z = u + i v , encontramos $$e^{i \gamma z} = e^{i \gamma (u+iv) } = e^{i \gamma u} e^{ – \gamma v}$$ Como \gamma > 0 , a exponencial e^{i \gamma z} vai a zero quando v \rightarrow \infty e, assim, devemos fechar o contorno por cima. Logo, $$  \oint\limits_{C}{\frac{e^{i \gamma z}}{1 + z^4} dz } = 2 \pi i \sum\limits_{k=0}^{1}{ \left[ \text{Res} \left( \frac{e^{i \gamma z} }{1 + z^4} \right) \right]_{z = u_k}} = \\ = 2 \pi i \left[ \lim_{z \rightarrow u_0}{\frac{e^{i \gamma z} }{\frac{d}{dz} (1 + z^4)}  } +  \lim_{z \rightarrow u_1}{\frac{e^{i \gamma z} }{\frac{d}{dz} (1 + z^4)}  } \right] = \frac{i \pi }{2} \left( \frac{e^{i \gamma u_0} }{u_0^3} + \frac{e^{i \gamma u_1} }{u_1^3}   \right).$$

Daí, $$\int\limits^{\infty}_{-\infty}{\frac{e^{i \gamma u}}{1 + u^4} du } + \lim_{R \rightarrow \infty }{\int_{C_R}{\frac{e^{i \gamma z}}{1 + z^4} dz } } = \frac{i \pi }{2} \left( \frac{e^{i \gamma u_0} }{u_0^3} + \frac{e^{i \gamma u_1} }{u_1^3}   \right).$$ Portanto, $$\int\limits^{\infty}_{-\infty}{\frac{e^{i \gamma u}}{1 + u^4} du } = \frac{i \pi }{2} \left( \frac{e^{i \gamma u_0} }{u_0^3} + \frac{e^{i \gamma u_1} }{u_1^3}   \right). \tag{1}$$

Agora consideramos \gamma < 0 e como e^{i \gamma z} vai a zero quando |z| \rightarrow  \infty devemos fechar o contorno por baixo, ou seja, v \rightarrow - \infty .

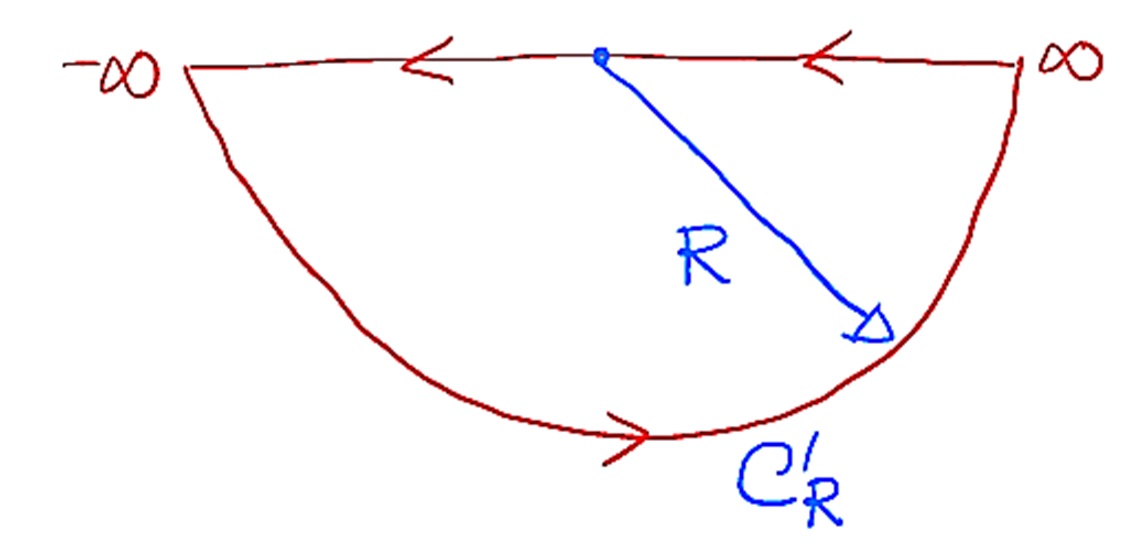
Assim, $$  \oint\limits_{C}{\frac{e^{i \gamma z}}{1 + z^4} dz } = 2 \pi i \sum\limits_{k=2}^{3}{ \left[ \text{Res} \left( \frac{e^{i \gamma z} }{1 + z^4} \right) \right]_{z = u_k}} = \\ = 2 \pi i \left[ \lim_{z \rightarrow u_2}{\frac{e^{i \gamma z} }{\frac{d}{dz} (1 + z^4)}  } +  \lim_{z \rightarrow u_3}{\frac{e^{i \gamma z} }{\frac{d}{dz} (1 + z^4)}  } \right] \Rightarrow \\ \Rightarrow \int\limits^{\infty}_{-\infty}{\frac{e^{i \gamma u}}{1 + u^4} du } + \lim_{R \rightarrow \infty }{\int_{C’_R}{\frac{e^{i \gamma z}}{1 + z^4} dz } } = \frac{i \pi }{2} \left( \frac{e^{i \gamma u_2} }{u_2^3} + \frac{e^{i \gamma u_3} }{u_3^3}   \right).$$ Portanto, $$\int\limits^{\infty}_{-\infty}{\frac{e^{i \gamma u}}{1 + u^4} du } = – \frac{i \pi }{2} \left( \frac{e^{i \gamma \overline{u_0}} }{\overline{u_0}^3} + \frac{e^{i \gamma \overline{u_1}} }{\overline{u_1}^3}   \right). \tag{2}$$

Combinando as equações (1) e (2), temos que para qualquer \gamma $$\int\limits^{\infty}_{-\infty}{\frac{e^{i \gamma u}}{1 + u^4} du } = \frac{i \pi }{2} \left( \frac{e^{i | \gamma| u_0} }{u_0^3} + \frac{e^{i | \gamma | u_1} }{u_1^3}   \right).$$

Agora, observe que \begin{eqnarray} u_0 ^3 & = & \left( e^{\frac{ i \pi }{4} } \right)^3 = e^{\frac{ i 3 \pi }{4} } = \frac{\sqrt{2}}{2}(-1+i) \\ u_1 ^3 & = & \left( e^{\frac{ i 3\pi }{4} } \right)^3 = e^{\frac{ i 9 \pi }{4} } = \frac{\sqrt{2}}{2}(1+i) \\ i u_0 & = & i e^{i \frac{ \pi }{4}} =i  \frac{\sqrt{2}}{2}(1+i) = \frac{\sqrt{2}}{2}(-1+i)\\ i u_1 & = & i e^{i \frac{3 \pi }{4}} =i  \frac{\sqrt{2}}{2}(-1+i) = \frac{\sqrt{2}}{2}(-1-i)\end{eqnarray}

O que nos leva a $$  \frac{e^{i | \gamma| u_0} }{u_0^3} + \frac{e^{i | \gamma | u_1} }{u_1^3}   = \frac{2}{ \sqrt{2}} \left[  \frac{e^{| \gamma| \frac{\sqrt{2}}{2}(-1+i)} }{(-1+i)} + \frac{e^{ | \gamma | \frac{\sqrt{2}}{2}(-1-i) } }{(1+i)}  \right] = \\=-2 i e^{\frac{ \sqrt{2} }{2} | \gamma |} \text{ sen } \left( \frac{\sqrt{2}}{2} | \gamma | + \frac{ \pi }{4} \right) $$ Logo, $$\int\limits^{\infty}_{-\infty}{\frac{e^{i \gamma u}}{1 + u^4} du } = \pi  e^{\frac{ – \sqrt{2} }{2} | \gamma |} \text{ sen } \left( \frac{\sqrt{2}}{2} | \gamma | + \frac{ \pi }{4} \right) $$

Lembrando que $$ F(\alpha) = \frac{1}{2 |a|^3 \sqrt{2\pi}} \int\limits^{\infty}_{-\infty}{\frac{ e^{i|a| (\alpha + \beta ) u} + e^{i|a| (\alpha – \beta ) u}}{1 + u^4 } du}$$ podemos concluir que $$F( \alpha) = \frac{1}{2 |a|^3 \sqrt{2\pi}} \left[  e^ {- \frac{\sqrt{2} }{2} |a (\alpha + \beta ) | }  \text{ sen } \left( \frac{\sqrt{2}}{2} |a (\alpha + \beta )  | + \frac{ \pi }{4} \right) + \\ +  e^ {- \frac{ \sqrt{2} }{2} |a (\alpha – \beta ) | }  \text{ sen } \left( \frac{\sqrt{2}}{2} |a (\alpha – \beta )  | + \frac{ \pi }{4} \right) \right]. $$

Leia Mais:

• Transformada de Fourier | 1ª Lista de Exercícios Resolvidos
• Transformada de Fourier | Uma Introdução aos Conceitos Básicos
• Solução da Equação da Onda Usando a Transformada de Laplace
• Identidade de Parseval | Séries, Integrais e Transformadas de Fourier

Bibliografia do Artigo:

Basta clicar no título do livro para ver o livro

1. SPIEGEL, M. R. – “Análise de Fourier”.
2. KREYSZIG, E. –“Advanced Engineering Mathematics”.
3. BUTKOV, E. – “Física Matemática”