A Equação e os Polinômios de Legendre | Solução de E.D.O.’s Por Séries

A Equação de Legendre é uma E.D.O. de 2ª Ordem que aparece em estudos avançados de matemática aplicada na física e na engenharia. Neste artigo solucionamos esta equação.

A Equação de Legendre é a equação diferencial ordinária de segunda ordem dada por \left( 1-x^2 \right)y'' - 2xy' + n(n+1)y = 0 \tag{1} . Na resolução iremos considerar somente o caso em que n é um inteiro não-negativo. Como procuramos soluções seriais (na forma de série infinita) de cada equação em torno de x=0 , observamos que a origem é um ponto ordinário da equação de Legendre.

O parâmetro n na equação de Legendre é um número real dado e cada uma das soluções desta equação é chamada de função de Legendre. Observe que a equação pode ser reescrita como $$ \left[ \left( 1-x^2 \right)y’ \right]’ + n \left(n+1 \right) y = 0 \tag{2}.$$

Quem Foi Legendre?

Adrien-Marie Legendre (nascido em 18 de setembro de 1752, Paris , França – falecido em 10 de janeiro de 1833, Paris) foi um matemático francês cujo trabalho distinto em integrais elípticas forneceu ferramentas analíticas básicas para a física matemática. Pouco se sabe sobre o início da vida de Legendre, exceto que a riqueza de sua família lhe permitiu estudar física e matemática , a partir de 1770, no Collège Mazarin (Collège des Quatre-Nations) em Paris e que, pelo menos até a Revolução Francesa, ele não teve que trabalhar.

No entanto, Legendre ensinou matemática na École Militaire em Paris de 1775 a 1780. Em 1782 ele ganhou um prêmio oferecido pela Academia de Ciências de Berlim por seu esforço para “determinar a curva descrita por balas de canhão e bombas, levando em consideração a resistência do ar e dar regras para obter as faixas correspondentes a diferentes velocidades iniciais e a diferentes ângulos de projeção.” No ano seguinte, ele apresentou pesquisas sobre mecânica celeste à Academia Francesa de Ciências , e logo foi recompensado com a adesão.

Em 1787 ele se juntou à equipe francesa, liderada por Jacques-Dominique Cassini e Pierre Mechain, nas medições geodésicas realizadas em conjunto com o Royal Greenwich Observatory em Londres. Nessa época, ele também se tornou membro da British Royal Society . Em 1791 ele foi nomeado junto com Cassini e Mechain para um comitê especial para desenvolver osistema métrico e, em particular, realizar as medições necessárias para determinar o medidor padrão . Ele também trabalhou em projetos para produzir tabelas logarítmicas e trigonométricas .

Resolvendo a Equação de Legendre Usando Séries de Potências

Dividindo a equação (1) por 1 - x^2 encontramos a equação y'' - \frac{2x}{\left( 1-x^2 \right)} y' + \frac{n(n+1)}{\left( 1-x^2 \right)} y = 0 \tag{3} que está na forma canônica do Teorema da Existência de Soluções em Série de Potências. Além disso, podemos ver que os coeficientes da equação resultante são analíticas em x=0, o que nos permite aplicar o método das séries de potências.

Substituindo $$y = \sum_{m=0}^{\infty}{c_m  x ^m} \label{4} $$ e suas derivadas na equação (1) e denotando a constante n (n+1) por k nós obtemos $$ \left( 1-x^2 \right) \sum_{m=2}^{\infty}{m(m-1)c_{m}  x ^{m-2}} – 2x \sum_{m=1}^{\infty}{m c_{m}  x ^{m-1}} + k \sum_{m=0}^{\infty}{c_{m}  x ^{m}} = 0 $$ que nos leva a $$ \sum_{m=2}^{\infty}{m(m-1)c_{m}  x ^{m-2}} – \sum_{m=2}^{\infty}{m(m-1)c_{m}  x ^{m}}  – 2 \sum_{m=1}^{\infty}{m c_{m}  x ^{m}} + k \sum_{m=0}^{\infty}{c_{m}  x ^{m}} = 0 .$$

Expandindo alguns termos para colocar todas as séries começando na potência x^2 encontramos $$ = \left[ n(n+1) c_0 + 2 c_2 \right] x^0 + \left[ n(n+1) c_1 + 2 c_1 + 6 c_3 \right] x^1  + \\ + \sum_{m=4}^{\infty}{m(m-1)c_{m}  x ^{m-2}} – \sum_{m=2}^{\infty}{m(m-1)c_{m}  x ^{m}}  – 2 \sum_{m=2}^{\infty}{m c_{m}  x ^{m}} + k \sum_{m=2}^{\infty}{c_{m}  x ^{m}} = 0.$$

Agora, fazendo j = m - 2 na primeira série,  j = m nas demais, e lembrando que k = n (n+1) que encontramos $$ = \left[ n(n+1) c_0 + 2 c_2 \right]  + \left[ (n-1)(n+2) c_1 + 6 c_3 \right] x  + \\ + \sum_{j=2}^{\infty}{\left[ (j+2)(j+1)c_{j+2} + (n-j)(n+j +1) c_j \right]x^{j}} = 0.$$ Daí, como a soma dos coeficientes de cada potência de x tem que ser zero, encontramos o sistema \begin{eqnarray} n(n+1)c_0 + 2 c_2 & = & 0  \\  (n-1)(n+2)c_1 + 6 c_3 & = & 0 \\ (j+2)(j+1)c_{j+2} + (n-j)(n+j+1)c_j & = & 0 \end{eqnarray}  o que nos leva à fórmula de recorrência $$ c_2 = – \frac{n(n+1)}{2!} c_0 $$ $$ c_3 = – \frac{(n-1)(n+2)}{3!} c_1 $$ $$ c_{j+2} = – \frac{(n-j)(n+j+1)}{(j+2)(j+1)} c_j , \qquad j = 2,3,4, …\;\;\; . \tag{4} $$

Expandindo a fórmula em (4), obtemos um coeficiente dado pelo segundo coeficiente precedente, exceto por c_0 e c_1 , os quais são dados por constantes arbitrárias. Assim, $$c_2 = – \frac{n (n+1)}{2!}c_0 $$ $$c_3 = – \frac{(n-1) (n+2) }{3!}c_1 $$ $$c_4 = – \frac{(n-2) (n+3) }{4 \times 3}c_2  = \frac{(n-2) n (n+1) (n+3)}{4!}c_0$$ $$c_5 = – \frac{(n-3) (n+4) }{5 \times 4}c_3 = \frac{(n-3) (n-1) (n+2) (n+4) }{5!}c_1 $$ e sucessivamente todos os coeficientes poderão ser colocados em termos de c_0 e c_1 . Pelo menos em |x| < 1 , obtemos duas soluções linearmente independentes dadas em séries de potências por $$ y_1 (x) = c_0 \left[ 1 – \frac{n (n+1)}{2!} x^2 + \frac{(n-2) n (n+1) (n+3)}{4!} x^4 – \\ \frac{(n-4)(n-2) n (n+1) (n+3) (n+5) }{6!} x^6 + … \right] $$ $$ y_2 (x) = c_1 \left[ x – \frac{(n-1) (n+21)}{3!} x^3 + \frac{(n-3) (n-1) (n+2)(n+4)}{5!} x^5 – \\ \frac{(n-5)(n-3) (n-1) (n+2) (n+4) (n+6) }{7!} x^7 + … \right] .$$

Note que se n for um inteiro par, a primeira série é finita, enquanto y_2 (x) é uma série infinita. Por exemplo, se n = 4 , então $$y_1(x) = c_0 \left[ 1 – 10 x^2 + \frac{35}{3} x^4 \right].$$ Analogamente, quando n foir um inteiro ímpar, a série para y_2 (x) termina com x^n ; isto é, quando n for um inteiro não negativo, obtemos uma solução polinomial de grau n da equação de Legendre.

Como qualquer múltiplo de uma solução para a equação de Legendre é também uma solução, é tradicional escolher valores específicos para c_0 e c_1 , dependendo do inteiro positivo n , se n for par e ímpar, respectivamente. Para n = 0 , escolhemos c_0 = 1 e para n = 2,4,6,... $$c_0 = (-1)^{n/2} \frac{1 \times 2 \times … \times (n-1)}{2 \times 4 \times … \times n} $$ enquanto que para n=1 , escolhemos  c_1 = 1 e para n = 3,5,7,... $$ c_1 = (-1)^{(n-1)/2} \frac{1 \times 3 \times … \times n}{2 \times 4 \times … \times (n-1)} .$$ Por exemplo, quando n = 4 , temos $$y_1 (x) = \frac{1}{8} \left( 35 x^4 – 30 x^2 + 3 \right) .$$

No caso geral, inserindo os coeficientes na solução geral dada em (4), a solução da equação de Legendre é dada por $$ y(x) = c_0 y_1 (x) + c_1 y_2 (x) $$ no intervalo -1 < x <1 . A solução resultante da equação de Legendre é denominada polinômio de Legendre de grau n e é denotado por P_n (x) , que é dada por $$ P_n (x) = \sum_{m=0}^{M}{(-1)^m \frac{(2n – 2m)! }{2^n m! (n-m)!(n-2m)!} x^{n-2m} } $$ onde M = \dfrac{n}{2} ou \dfrac{(n-1)}{2} qualquer que seja o valor do inteiro M .

Os Polinômios de Legendre

Em várias aplicações, o parâmetro n na equação de Legendre sera um inteiro não negativo. Então se n é par, y_1 (x) reduz a um polinômio de grau n . Por outro lado, se n é ímpar, o mesmo é verdade com respeito a y_2 (x) . Estes polinomios, multiplicados por alguma constante, são chamados de polinômios de Legendre.

Estes polinômios de Legendre são denotados por P_n (x) , através das séries de y_1 (x) e y_2 (x) e pelas escolhas de c_0 e c_1 , encontramos os polinômios de Legendre, ou seja, $$ P_0 (x) = 1, \qquad P_1(x) = x, \qquad P_2 (x) = \frac{1}{2} \left( 3 x^2 – 1 \right), $$ $$ P_3 (x) = \frac{1}{2} \left( 5 x^3 – 3x \right), \qquad P_4 (x) = \frac{1}{8} \left( 35 x^4 – 30 x^2 +3 \right), $$ $$ P_5 (x) = \frac{1}{8} \left( 63 x^5 – 70 x^3 + 15 x \right).$$

Lembre-se que P_0 , P_1 , P_2 , P_3 , ... são soluções particulares para as equações diferenciais \begin{eqnarray} n=0 & , & (1-x^2 ) y” – 2x y’ = 0 \\ n=1 & , & (1-x^2 ) y” – 2x y’ +2y = 0 \\ n=2 & , & (1-x^2 ) y” – 2x y’+6y = 0 \\ n=3 & , & (1-x^2 ) y” – 2x y’ + 12 y = 0 \end{eqnarray}. Abaixo temos os gráficos dos 14 primeiros polinômios de Legendre no intervalo -1 < x <1 :

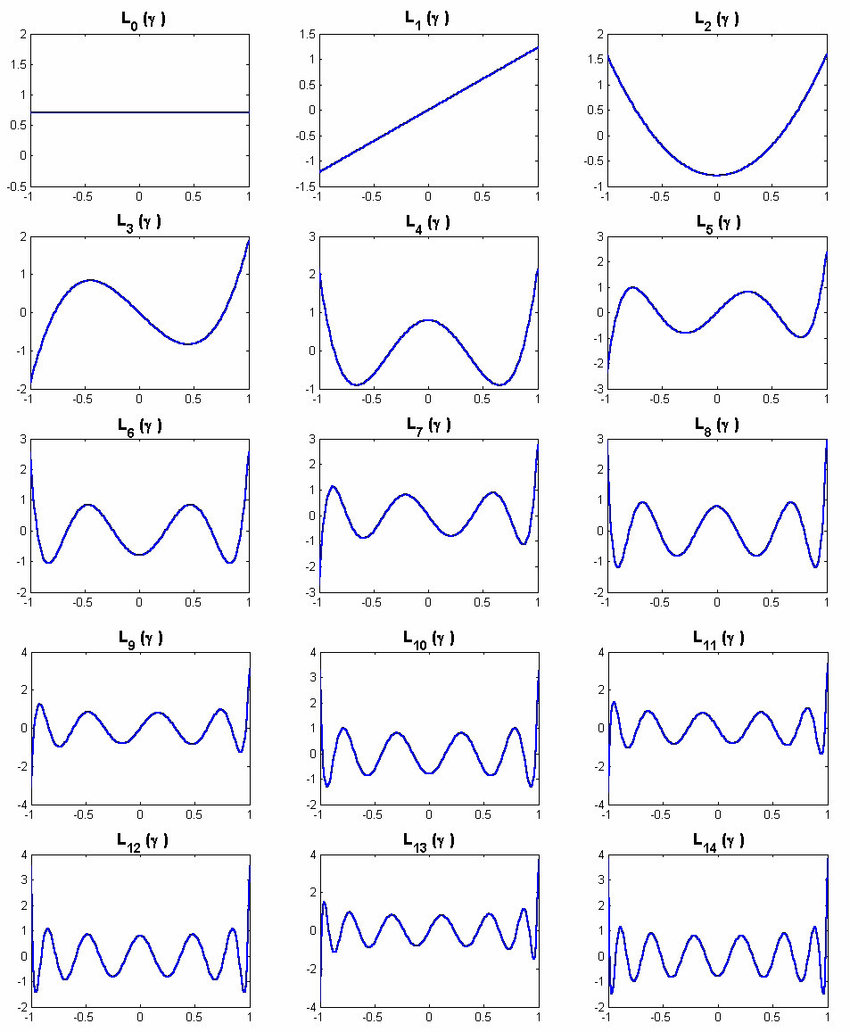
PROPRIEDADES DOS POLINÔMIOS DE LEGENDRE

As seguintes propriedades dos polinômios de Legendre podem ser facilmente verificadas a partir de P_0 , P_1 , P_2 , P_3 , ... e dos gráficos:

1. P_n (-x) = (-1)^n P_n (x) . Esta propriedade significa que P_n (x) é uma função par ou ímpar, dependendo de n ser par ou ímpar;
2. P_n (1) = 1 ;
3. P_n (-1 ) = (-1)^n ;
4. P_n (0) = 0 com n = 1,3,5,... ;
5. P' _n (0) = 0 , onde n = 0,2,4,... .

Relação de Recorrência

Relações de recorrência que relacionam polinômios de Legendre de diferentes graus são muito importantes em alguns aspectos de suas aplicações. Reduzimos uma dessas relações usando a fórmula $$ (1-2xt+t^2)^{-1/2} = \sum_{n=0}^{\infty}{P_n ( x) t^n} \label{5} .$$ A função da esquerda é chamada de função geradora dos polinômios de Legendre.

Partindo desta equação, derivando em ambos os lados em relação a t , multiplicando por 1 -2xt + t^2 termo a termo e observando os cancelamentos apropriados, simplificando e trocando os índices de soma, após igualar o coeficiente de t^k a zero, conseguiremos a seguinte relação: $$ (k+1)P_{k+1} (x) – [2k+1]P_k (x) + k P_{k-1} (x) = 0, \qquad k=2,3,4,… \tag{6}$$ que é uma fórmula válida também quando k = 1 (este processo pode ser detalhadamente encontrado no primeiro livro das referências bibliográficas).

Se, digamos, quisermos encontrar o polinômio P_6 (x) , podemos usar a fórmula (6) com k = 5 . Essa relação expressa então P_6 (x) em termos de quantidades conhecidas de P_4 (x) e P_5 (x) .

Livros-texto usados no artigo

1. “Equações Diferenciais: Volume 1” – Dennis G. Zill e Michael R. Cullen
2. Erwin Kreyszig – “Advanced Engineering Mathematics” | Link do Livro

Listas de Exercícios Resolvidos Sobre Soluções de E.D.O.’s por Séries

• E.D.O.’s e as Séries de Potências | 1ª Lista de Exercícios Resolvidos
• E.D.O.’s e as Séries de Potências | 2ª Lista de Exercícios Resolvidos

Leia Mais:

• Solução de Equações Diferenciais Ordinárias por Séries de Potência
• E.D.O.’s Por Séries de Potência | Solução em Torno de Pontos Ordinários
• O que são Séries de Potências? Definição, Convergência e Exemplos.
• Séries de Potências | 1ª Lista de Exercícios Resolvidos
• Séries de Fourier | História, Definição e Condições de Convergência.