PRECISANDO DE AJUDA COM SEUS EXERCÍCIOS SOBRE ESTE CONTEÚDO? Entre em contato com a gente via WhatsApp clicando aqui. |
A função Gama é importante em matemática pura e aplicada, ciência e engenharia, incluindo aplicações que envolvem a condução de calor em lasers e tecidos humanos. Em estatística, a função gama é utilizada para calcular a função de densidade de probabilidade e função de distribuição acumulada da distribuição gama, que pode ser usada para descrever os dados positivamente assimétricos.
As funções Gama, Gama incompleta e logaritmo natural gama estendem a generalizam a função fatorial f(n) = n! , para que “fatoriais” possam ser calculadas para as números irracionais e frações.
Em aplicações computacionais a função logaritmo natural gama às vezes é usada, pois apresenta menos probabilidade de gerar números grandes que possam ser maiores do que a capacidade de armazenamento, gerando menos custo computacional.
A Definição da Função Gama
A definição de Euler para a função Gama, definida por ele em seu texto “Instituitiones Calculi Integralis”, publicado em 1768, é dada por $$ \Gamma (x) = \int_{0}^{ \infty}{t^{x-1}e^{-t} dt}.$$ A convergência desta integral requer x-1 > -1 , ou seja, x >0 .
A relação de recorrência $$\Gamma (x+1) = x \Gamma (x),$$ pode ser obtida à partir à partir desta definição usando a técnica de integração por partes.
Embora a a condição de convergência diga o contrário, e a integral que define a função gama não convirja para x < 0 , é possível mostrar através de definições alternativas que a função gama é definida para todos os valores reais e complexos, exceto para os inteiros não-positivos.
Desta forma, a relação de recorrência $$\Gamma (x+1) = x \Gamma (x)$$ é válida todo x \neq - n , sendo n = 0, 1, 2, 3, 4, … .
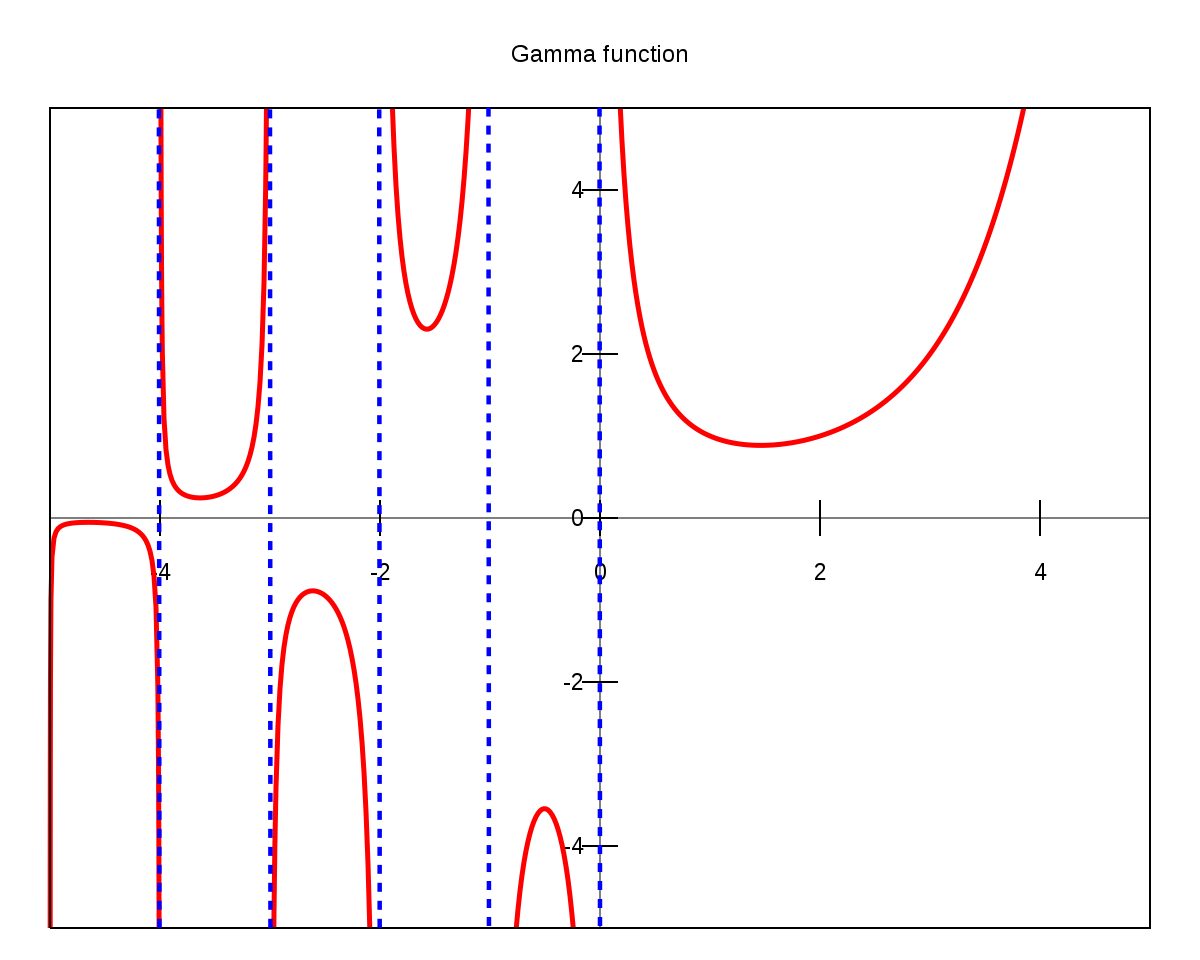
Sendo assim, \Gamma (x) é considerada uma função real e seu gráfico é dado abaixo. Observe que todos os inteiros não positivos determinam assíntotas verticais no gráfico da função gama.
O Fatorial Generalizado
Quando x= 1 , temos $$ \Gamma (1) = \int_{0}^{ \infty}{e^{-t} dt}.= 1$$ e pela fórmula de recorrência acima $$ \Gamma (2) = 1 \Gamma (1) = 1$$ $$ \Gamma (3) = 2 \Gamma (2) = 2 \times 1$$ $$ \Gamma (4) = 3 \Gamma (3) = 3 \times 2 \times 1$$ e assim por diante. Desta maneira, vemos que quando n é número inteiro positivo, $$ \Gamma (n) = n! $$
Por esta razão, a função Gama é frequentemente chamada de fatorial generalizado.
Assim, a função gama nada mais é do que uma extensão do nosso já conhecido fatorial, dado através da definição abaixo:
DEFINIÇÃO:
Para todo real \alpha > -1 definimos o fatorial de \alpha por $$ \alpha ! = \Gamma (\alpha +1) . $$
Abaixo, construímos uma tabela com o auxílio do software xMaxima:
| \alpha | -0,99 | -0,9 | -0,1 | 0 | 0,4 | 0,45 | 0,5 | 0,6 | 1 | 2,5 | 3 |
| \alpha ! | 99,4325 | 9,5135 | 1,0686 | 1 | 0,8873 | 0,8856 | 0,8862 | 0,8935 | 1 | 3,3233 | 6 |
A Função Gama Incompleta
A função Gama incompleta, \gamma , é uma variação da função gama completa definida por uma integral com um limite superior finito, e não infinito. Para um dado número a e um limite superior x ,
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
$$ \gamma (x,a) = \int_{0}^{ x}{t^{a-1}e^{-t} dt}.$$
A Função Logaritmo Natural Gama
Por sua vez, a função logaritmo natural gama, \ln \left( \Gamma (z) \right) é o logaritmo natural da função gama completa, ou seja,
$$\ln \left( \Gamma (x) \right) = \ln \left( \int_{0}^{ \infty}{t^{x-1}e^{-t} dt} \right).$$
sendo uma função convexa definida apenas para números positivos.
Fórmula Assintótica para a Função Gama
Se n é grande, são evidentes as dificuldades inerentes ao cálculo de \Gamma (n) . A relação a seguir constitui um resultado útil em tais casos: $$ \Gamma (n+1) = \sqrt{2 \pi n} n^n e^{-n} e^{\frac{ \theta }{12(n+1)}} \qquad 0 < \theta < 1 .$$ Para quase todos os fins práticos, podemos omitir o último fator, que é muito próximo de 1. Se n é inteiro, podemos escrever $$ n! \approx \sqrt{2 \pi n} n^n e^{-n}$$ que é por vezes denominada aproximação fatorial de Stirling (ou fórmula assintótica) para n! .
