Se você está estudando elipses como uma curva gerada por seções cônicas e tendo problemas, não se preocupe! Este artigo oferecerá explicações claras para ajudá-lo a compreender as propriedades e equações das elipses.

A elipse é uma forma geométrica que é formada cortando um cone em um ângulo. Tem um conjunto único de propriedades e equações que o tornam um assunto fascinante em matemática. Neste guia, exploraremos os fundamentos das elipses e sua equações
O que são seções cônicas?
As seções cônicas são as curvas que resultam da interseção de um plano e um cone. O cone pode ser um cone circular reto ou um cone oblíquo. As curvas resultantes são classificadas em quatro tipos: círculos, elipses, parábolas e hipérboles. Cada tipo de curva tem suas próprias propriedades e aplicações únicas em matemática e física. As parábolas, em particular, têm uma propriedade foco-diretriz que as torna úteis em óptica e comunicação por satélite.

O que é uma elipse e como ela é definida?
Uma elipse é uma curva fechada que é formada cortando um cone em um ângulo que não é perpendicular à base. Possui dois focos, que são pontos dentro da elipse equidistantes do centro. O eixo maior é o diâmetro mais longo da elipse, enquanto o eixo menor é o diâmetro mais curto. A distância entre os focos é chamada de distância focal e é igual ao comprimento do eixo maior. A excentricidade de uma elipse é uma medida de quão alongada ela é, e é definida como a razão entre a distância entre os focos e o comprimento do eixo maior.
| Os livros usados como referência deste artigo sobre Norma e Produto Escalar de Vetores no Plano são dados abaixo: | ||
Construindo uma Elipse
Um elipse com focos F e F' é o conjunto dos pontos P do plano cuja somas das distâncias a F e F' é igual uma constante denotada por 2a . É conveniente escolher um sistema de eixos tal que os os focos tenham coordenadas F(c,0) e F' (-c,0) . A distância 2c entre os focos é chamada de distância focalda eleipse.

| 
|
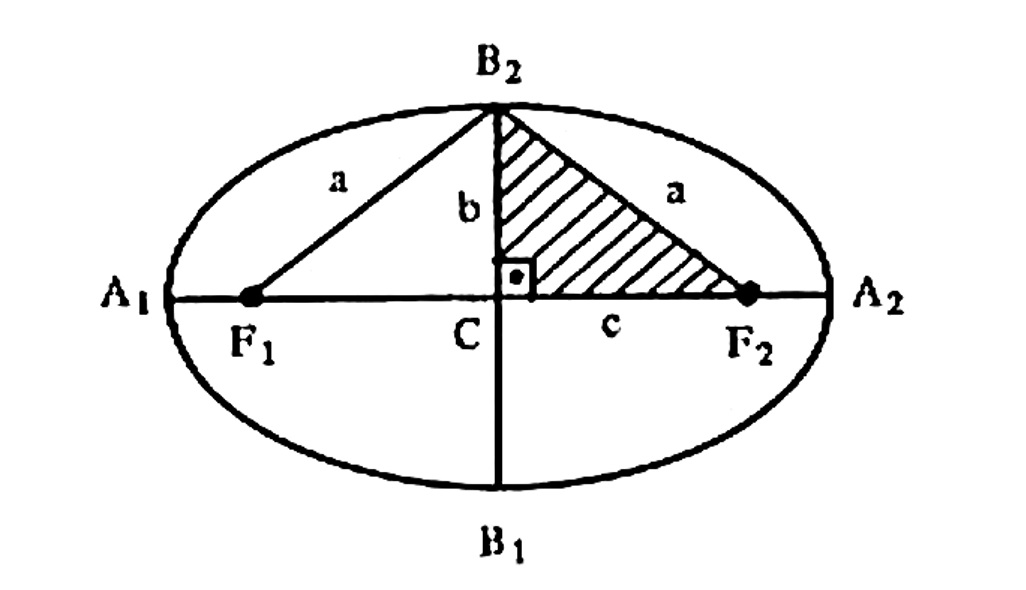
Elementos da Elipse
Considerando a figura abaixo, temos:

- Focos: são os F_1 e F_2 ;
- Distância Focal: é a distância 2c entre os focos;
- Centro: é o ponto médio C do segmento F_1 F_2 ;
- Eixo Maior: é o segmento A_1 A_2 de comprimento 2a (que contém os focos e os seus extremos pertencem à elipse);
- Eixo Menor: é o segmento B_1 B_2 de comprimento 2b (perpendicular ao eixo maior passando pelo seu ponto médio);
- Vértices: são os pontos A_1 , A_2 , B_1 e B_2 .
- Excentricidade: é o número dado por e = \dfrac{c}{a} . Tendo em vista que c<a , tem-se: 0 < e < 1 .
Observação: Em todo a elipse vale a relação $$a^2 = b^2 + c^2.$$ Na verdade, esta igualdade é a relação de Pitágoras no triângulo retângulo B_2 C F_2 .
A Equação da Elipse – O Caso mais Simples: vértice na origem do sistema
Um elipse com focos F_1 e F_2 é o conjunto dos pontos P do plano cuja somas das distâncias a F_1 e F_2 é igual uma constante denotada por 2a .
Eixo maior da elipse esta sobre o eixo Ox:
Um ponto P(x,y) pertence à elipse com focos F_1 (-c,0) e F_2 (c,0) , quando $$ d(P,F_1)+d(P,F_2) = 2a $$ isto é $$\sqrt{(x-c)^2 +(y-0)^2} + \sqrt{(x+c)^2 +(y-0)^2} = 2a $$ $$\sqrt{(x-c)^2 +y^2} = 2a – \sqrt{(x+c)^2 +y^2}$$ Elevando ambos os membros ao quadrado, obtemos $$ (x-c)^2 +y^2 = 4a^2 – 4a\sqrt{(x+c)^2 +y^2}+ (x+c)^2 +y^2$$ que, após simplificações, resulta $$ a \sqrt{(x+c)^2 +y^2} = a^2 +cx.$$ Elevando novamente ao quadrado: $$ a^2 (x^2+2cx+c^2 +y^2) = a^4 +2a^2cx+c^2 x^2,$$ e daí, $$(a^2-c^2)x^2+a^2y^2 = a^2 (a^2 – c^2).$$ É usual representar a diferença a^2 - c^2 por b^2 . A equação pode então ser escrita na forma $$b^2x^2 +a^2 y^2 = a^2 b^2.$$ Dividindo ambos os membros por a^2 b^2 obtemos finalmente $$ \frac{x^2}{a^2}+ \frac{y^2}{b^2} = 1,$$ que é a forma mais usual de escrever a equação da elipse, chamada de equação reduzida da elipse de centro na origem e eixo maior sobre o eixo dos x .
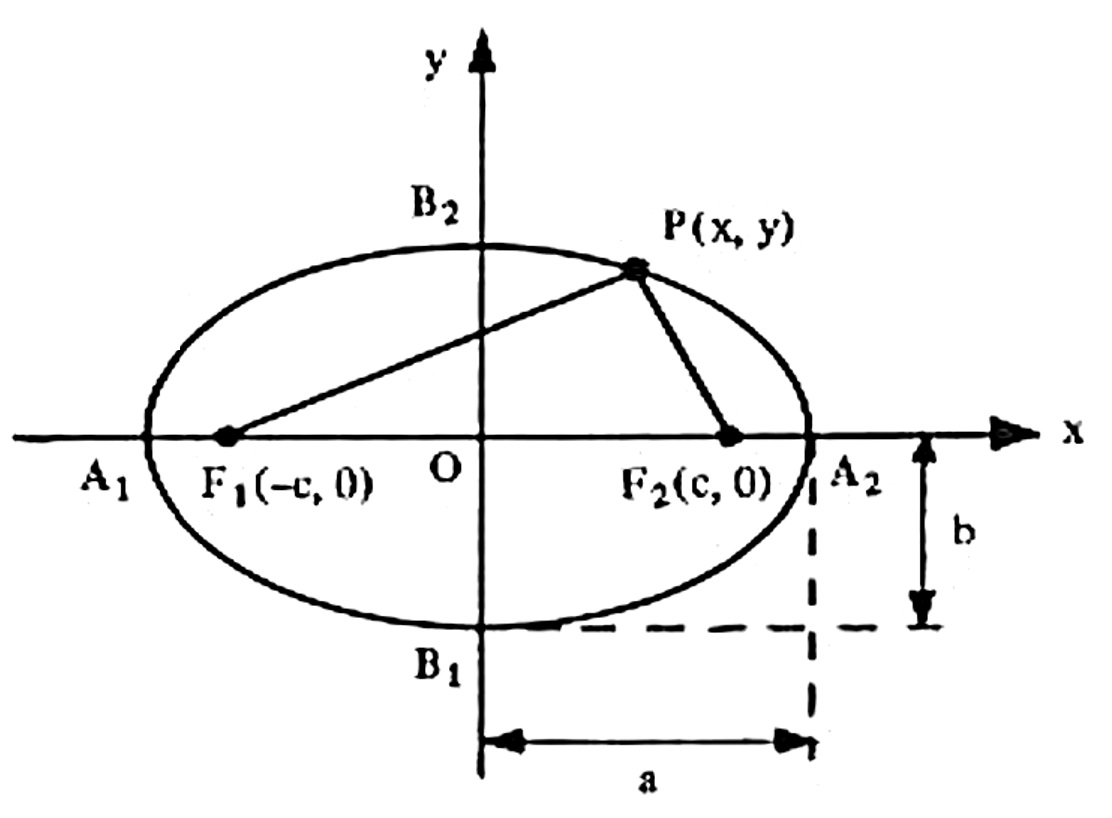
É fácil verificar que os pontos A_2(a,0) , A_1(-a,0) , B_2(0,b) e B_1(0,-b) (chamados de vértices) pertencem à elipse. Os segmentos A_1 A_2 e B_1 B_2 são eixos de simetria da elipse e são chamados de eixo maior (ou focal) e eixo menor (ou transverso).
Eixo maior da elipse esta sobre o eixo Oy:
Com procedimento análogo ao caso anterior encontraremos a equação reduzida $$ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 .$$

Observação: Tendo em vista que a^2 = b^2 + c^2 , segue-se que a^2 > b^2 \Rightarrow a > b . Então, sempre o maior dos denominadores na equação reduzida representa o número a^2 , onde a é medida do semi-eixo maior. Ainda mais: se na equação da elipse o número a^2 é denominador de x^2 , a elipse tem seu eixo maior sobre o eixo dos x .
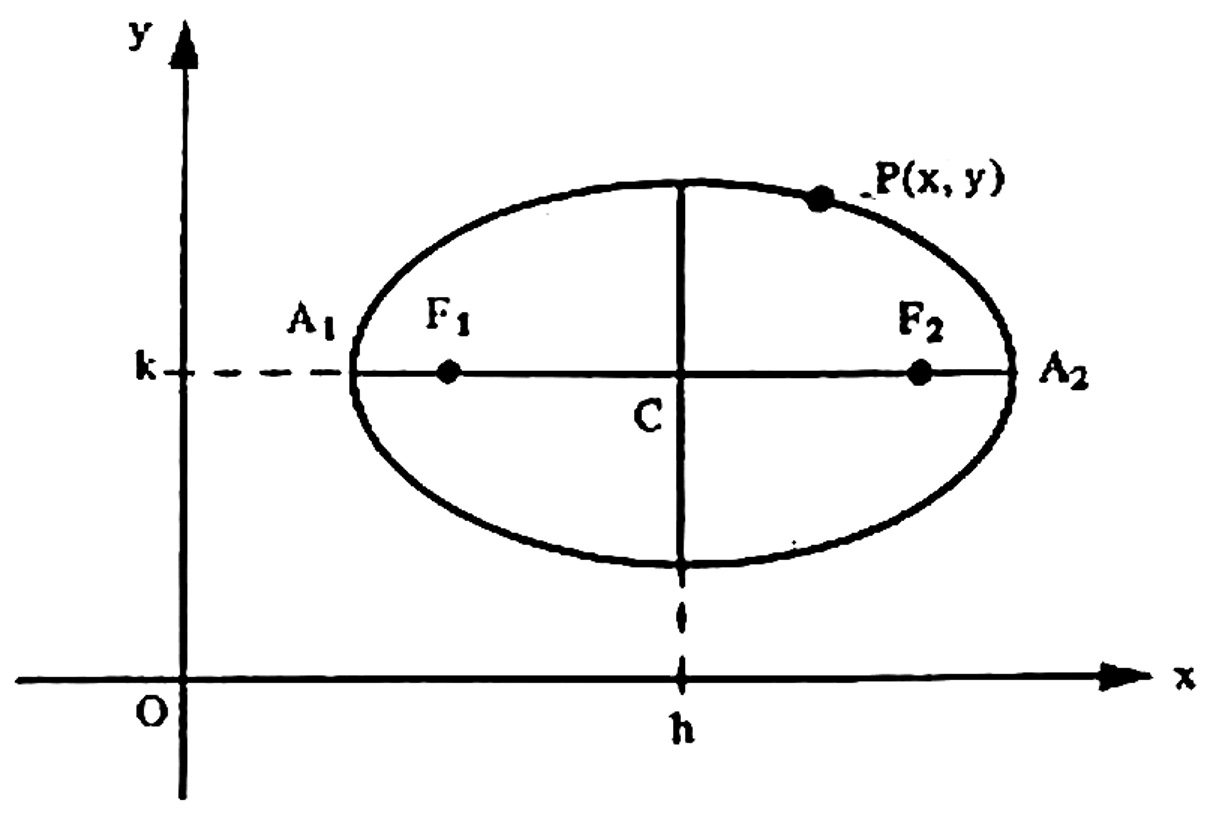
Equação da Elipse: A Translação de Eixos
Consideremos no plano cartesiano xOy num ponto O'(h,k) , arbitrário. Vamos introduzir um novo sistema x'Oy' tal que os eixos Ox' e Oy' tenham a mesma unidade de medida, a mesma direção e o mesmo sentido dos eixos Ox e Oy . Nesta condições, um sistema pode ser obtido do outro, através de uma translação de eixos.

Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Seja P um ponto qualquer do plano tal que suas coordenadas são:
- x e y em relação ao sistema xOy ;
- x' e y' em relação ao sistema x'Oy' ;
Pela figura acima, obtem-se $$ x = x’ + h \qquad y = y’+k$$ ou $$ x’ = x-h \qquad y’ = y – k $$ que são as formas de translação e que permitem transformar coordenadas de uma siste ma para outro, sendo que, a principal finalidade da transformação de coordenadas é modificar a forma de equações.
A Equação da Elipse de Vértices Fora da Origem do Sistema
1º Caso: O eixo maior da elipse é paralelo ao eixo dos x: Seja uma elipse com centro V(h,k) e eixo maior paralelo ao eixo dos x , sendo h e k coordenadas de V em relação ao sistema xOy . Seja P(x,y) um ponto qualquer da elipse. Considerando um novo sistema x'Oy' é $$\frac{x’^2}{a^2}+ \frac{y’^2}{b^2} = 1$$ mas, como $$ x’ = x-h \qquad y’ = y – k $$ então a equação da elipse com centro em V(h,k) e eixo paralelo ao eixo dos y é dada por $$\frac{(x-h)^2}{a^2}+ \frac{(y-k)^2}{b^2} = 1$$ e chamada de forma padrão da equação da elipse.
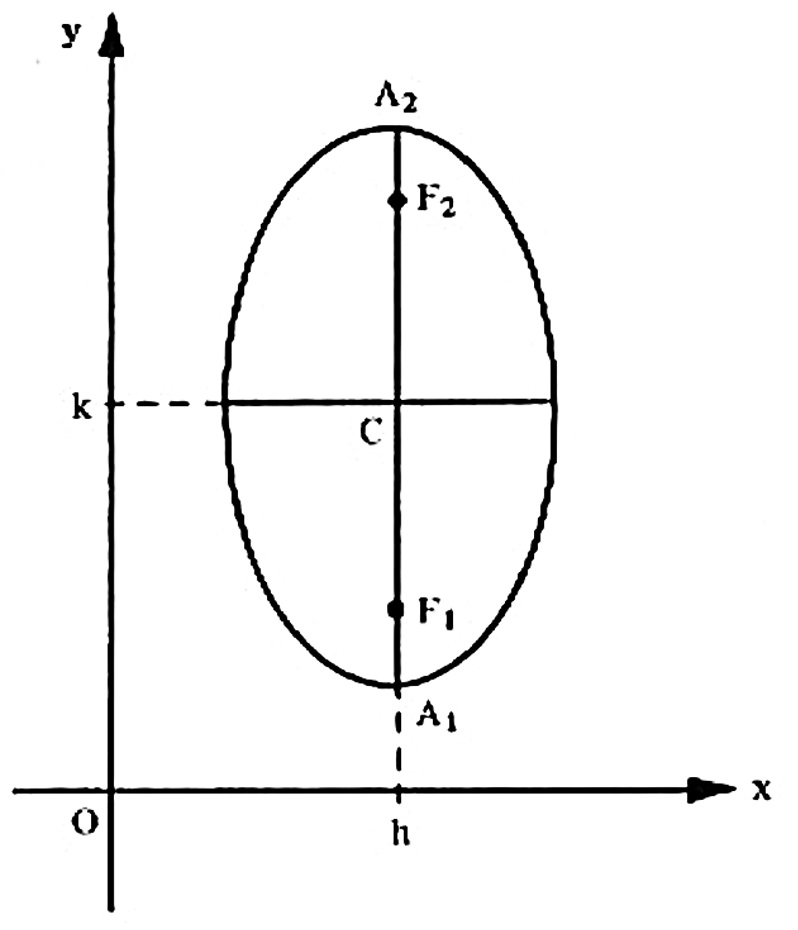
2º Caso: O eixo maior da elipse é paralelo ao eixo dos y: De modo análogo ao caso anterior, teremos: $$\frac{(x-h)^2}{b^2}+ \frac{(y-k)^2}{a^2} = 1.$$
Leia Mais Sobre Geometria Analítica
- Compreendendo as Seções Cônicas: Um Guia Introdutório
- A Parábola: Um estudo desta curva como seção cônica
- Retas No Plano Cartesiano: Posições Relativas Entre Retas
- Retas no Plano Cartesiano: Equações Reduzida, Geral, Vetorial e Paramétrica
- Vetores no Plano R²: Norma e Produto Escalar
- Vetores no R² | Um guia ilustrado dos vetores no plano cartesiano


