Desafios de Matemática: 18 problemas para desafiar sua mente!

Procurando por desafios de matemática para exercitar seu pensamento lógico? Este guia oferece uma variedade de desafios para você testar suas habilidades matemáticas.

Se você está procurando por desafios de matemática para exercitar seu pensamento lógico, você veio ao lugar certo. Neste guia, você encontrará uma variedade de desafios matemáticos para testar suas habilidades e aprimorar seu conhecimento em matemática. Prepare-se para enfrentar problemas intrigantes e divertidos que irão desafiar sua mente.

Desafios de matemática são atividades e jogos que usam a matemática como base e/ou forma de solução e servem de grande ajuda para aprender a disciplina ao mesmo tempo que desenvolvem outras faculdades como dedução lógica, interpretação de texto.

Os desafios matemáticos podem ser vistos como um passatempo ou até mesmo uma brincadeira, dependendo de como são colocados para serem resolvidos. Outra forma de utiliza-los é como recurso didático. Inclusive, entre os recursos didáticos citados nos Parâmetros Curriculares Nacionais (PCN) destacam-se os ”jogos”.

Segundo os PCN, “não existe um caminho único e melhor para o ensino da Matemática, no entanto, conhecer diversas possibilidades de trabalho em sala de aula é fundamental para que o professor construa sua prática”.

Miguel de Guzmán expressa muito bem o sentido que essa atividade tem na educação matemática: ”O interesse dos jogos na educação não é apenas divertir, mas sim extrair dessa atividade matérias suficientes para gerar um conhecimento, interessar e fazer com que os estudantes pensem com certa motivação”.

Abaixo, disponibilizamos 11 destes desafios.

Estabelecendo Uma Rota

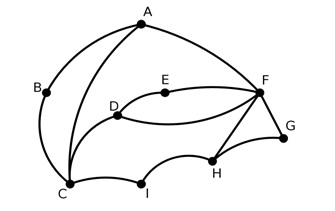
Um funcionário, encarregado de verificar, periodicamente, o estado das estradas, deseja planejar a sua rota de inspeção. Esta rota pode se iniciar em qualquer cidade e terminar em qualquer cidade.  Existe tal rota?

A Divisão do Vinho

Caminham juntos dois bêbados que compraram 8 litros de vinho de um bom taberneiro. Têm uma discussão a meio do caminho e decidem separar-se repartindo o vinho de forma igual. A única medida que têm é o barril de 8 litros onde transportam o vinho, uma vasilha de 5 LITROS e outra de 3 litros. Como devem fazer?

Desafio 3

Um Sheikh Árabe diz aos seus filhos para fazerem umDesafio 3 até a uma cidade distante para determinarem quem irá herdar a sua fortuna. Aquele que tiver o camelo mais lento vencerá. Os irmãos, depois de vaguearem sem destino durante dias, decidem aconselhar-se com um sábio. Imediatamente após ouvir o seu conselho, saltam para os camelos e correm o mais rapidamente que podem até a cidade. Que conselho lhes deu o sábio?

Um Problema de Raciocínio Lógico

Depois de morrer, Joãozinho se viu em uma sala com duas portas e dois guardas. Uma das portas o leva ao Céu, e a outra ao Inferno. Como Joãozinho era religioso, sempre quis ir para o céu desde sua primeira comunhão, ele tem que descobrir qual porta abrir: direita ou esquerda. Joãozinho também sabe que são pode fazer uma pergunta para qualquer um dos guardas. Os guardas a

Responderão de acordo com suas características: um sempre mente e o outro sempre fala a verdade. Contudo, não se sabem qual e qual. E agora? Você decide! Porta da direita ou porta da esquerda. Muito bem, quem se habilita a ajudar o pobre Joãozinho??

Lembrem-se:

1) Duas portas, uma saída.

2) Dois guardas idênticos — um mentiroso e um não.

3) Uma pergunta apenas para um dos guardas.

Construindo Estradas

Em certa região de um estado há 5 cidades. Será que é possível fazer estradas interligando as cidades de modo que cada cidade esteja interligada a exatamente 3 outras cidades?

Uma Pergunta de Matemática

Quantos números de 7 dígitos, maiores do que 6000000, podem ser formados usando apenas os algarismos 1, 3, 6, 6, 6, 8, 8?

Cores e Livros

Um artesão precisa colocar capas em 12 livros idênticos usando capas de cores vermelha, verde ou azul. De quantas maneiras ele pode fazer isto?

Um Estranho Jogo

Uma torre está no quadrado da extrema esquerda em uma tira  de quadrados e pode pular qualquer quantidade de quadrados para a direita em uma única jogada.

1. a) De quantas maneiras a o torre pode chegar ao quadrado da extrema direita?
2. b) De quantas maneiras a torre pode chegar ao quadrado da extrema direita em exatamente 7 jogadas?

Três Homens em Conflito

Três homens querem atravessar um rio. O barco que eles possuem suporta, no máximo, 130 quilogramas. Eles “pesam” 60, 65 e 80 kg. Como deve proceder para atravessar o rio sem afundar o barco?

Uma Conta de Matemática Difícil de Resolver

Três pessoas foram a um restaurante e no final a conta deu R$30,00. Cada um deles deu R$10,00 para pagar a conta.

O garçom levou o dinheiro até o caixa e o dono do restaurante disse o seguinte: Esses três são clientes antigos do restaurante, então vou devolver R$5,00 para eles! E entregou ao garçom cinco moedas de R$ 1,00. O garçom, muito esperto, fez o seguinte: pegou R$ 2,00 para ele e deu R$1,00 para cada um deles. No final ficou assim:

1ª pessoa: R$ 10,00 (– R$1,00 que foi devolvido) = gastou R$9,00.

2ª pessoa: : R$ 10,00 (– R$1,00 que foi devolvido) = gastou R$9,00.

3ª pessoa: :R$ 10,00 (– R$1,00 que foi devolvido) = gastou R$9,00.

Logo, se cada um deles gastou R$ 9,00, juntos gastaram R$ 27,00. E se o garçom pegou R$2,00 para ele, temos:

3 pessoas: R$27,00

Garçom: R$2,00

TOTAL: R$29,00

Onde foi parar o R$1,00?…

Lendo um Livro

Se eu leio 5 páginas por dia de um livro, eu termino de ler 16 dias antes do que se eu estivesse lendo 3 páginas por dia. Quantas páginas tem o livro?

Contando Quadrados

Quantos quadrados há na figura estilizada do rapaz com turbante?

Contando Quadrados – Parte 2

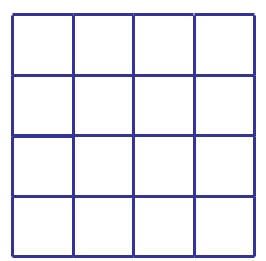
Quantos quadrados existem na figura abaixo?

Contando Triângulos Mágicos

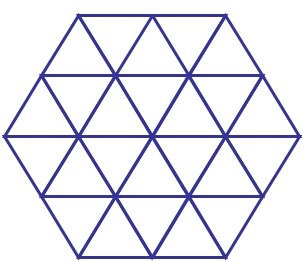
Quantos triângulos existem na figura?

Enigmas Matemáticos com Figuras

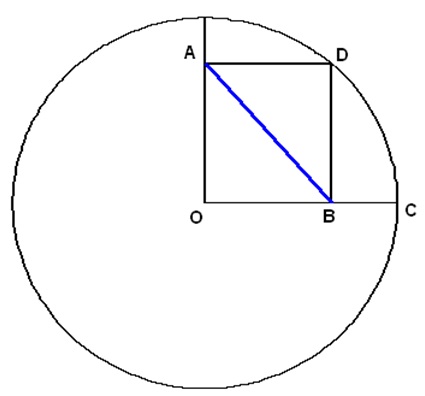
Se OC é um raio do círculo, OB = 4 cm, BC = 2 cm, O é o centro do círculo e ADBO é um retângulo, quanto mede AB?

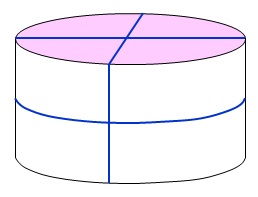
Dividindo o Bolo

Com apenas três cortes divida um bolo circular em 8 partes iguais.

Pinturas na Parede

Numa galeria de arte serão expostas obras de um artista famoso e excêntrico. Este artista fez uma pilha com diferentes pinturas, e periodicamente ele pegava uma delas e pendurava-a na parede.

Às 11:00, a pintura intitulada “número 30” foi pendurada.

Às 16:00, a pintura intitulada “número 240” foi pendurada.

Às 19:30, a pintura intitulada “número 315” foi pendurada.

Pergunta: Qual pintura o artista pendurará na parede às 21:20?

Um Vidro Cheio de Bactérias

Diversas bactérias estão colocadas em um vidro. Um segundo depois cada bactéria se divide em duas, no próximo segundo todas as bactérias se dividem novamente em duas, e assim por diante. Depois de um minuto, o vidro está cheio. Quando o vidro estava pela metade?

RESPOSTAS DOS NOSSOS DESAFIOS DE MATEMÁTICA E LÓGICA:

ESTABELECENDO UMA ROTA

Isso é um exercício de teoria de grafos.

Se a rota começa e termina em cidades diferentes, então tanto a cidade de partida como a de chegada devem ter um número ímpar de estradas.

Todas as outras cidades devem possuir um número par de estradas, pois toda vez que se chega a uma destas cidades, devemos sair dela por outra estrada.

Observe que os graus dos vértices A, D, F e H são ímpares (5 para F e 3 para as outras cidades). Logo tal rota não existe.

A DIVISÃO DO VINHO

Enchemos a vasilha de 3 litros. Passamos os 3 litros para a vasilha de 5 litros.

Enchemos novamente a vasilha de 3 litros.

Enchemos a vasilha de 5 litros com a de 3, pelo que nesta ficará um litro. V

azamos a vasilha de 5 no barril.

Passamos o litro da de 3 para a de 5.

Enchemos a vasilha de 3 e passamos o vinho desta para a de 5, que agora passa a ter 4 litros para um dos transportadores.

O barril tem também 4 litros para o outro transportador.

Desafio 3

“Troquem de Camelos”

UM PROBLEMA DE RACIOCÍNIO LÓGICO

Esse problema tem duas soluções:

1ª. Joaozinho deve fazer a pergunta ” Se eu perguntar ao outro guarda qual a porta para o céu, que porta vai ele me indicar ?” O guarda a quem perguntar, seja mentiroso ou não, vai indicar a porta para o inferno. Portanto Joaozinho deve seguir pela outra porta.

2ª Outra possibilidade será perguntar ” Se eu perguntar ao outro guarda qual a porta para o inferno, que porta vai ele me indicar ?” O guarda a quem perguntar, seja mentiroso ou não, vai indicar a porta para o ceu. Portanto Joaozinho deve seguir pela porta indicada.

CONSTRUINDO ESTRADAS

Suponhamos que seja possível. Considere o grafo no qual os vértices representam as cidades e as arestas as estradas. Assim, este grafo possui 5 vértices, onde cada um deles tem grau 3. Vamos contar o número de arestas neste grafo. Para isso, podemos somar os graus de todos os vértices. No entanto, nesta soma, cada aresta é contada duas vezes e assim, o número de arestas tem que ser igual a 5×3/2, que não é um número inteiro. Portanto, tal grafo não pode existir. Isto é, não é possível interligar as cidades da maneira pedida.

CORES E LIVROS

Arrumemos os 12 livros em uma fileira. Para determinar a distribuição das capas pelos livros, precisamos dividir a fileira em 3 grupos de livros usando 2 divisórias: o primeiro grupo receberá capas vermelhas, o segundo grupo receberá capas verdes e o terceiro grupo receberá capas azuis. Cada fileira composta de 12 livros e 2 divisórias corresponde, sem ambiguidade, a alguma maneira de distribuir as capas pelos livros. Portanto, o número de maneiras de distribuir as capas pelos livros é 91.

UM ESTRANHO JOGO

1. a) Como cada um dos 10 quadrados entre os quadrados da extrema esquerda e da extrema direita pode ser visitado ou não durante as jogadas, então a resposta é .
2. b) Arrumemos 11 bolas em uma fileira. Cada uma das bolas corresponde a um dos quadrados à esquerda do quadrado da extrema direita. Usando 6 divisórias precisamos dividir esta fileira em 7 grupos: o primeiro grupo corresponde aos quadrados que serão pulados na primeira jogada, o segundo corresponde aos quadrados que serão pulados na segunda jogada, e assim por diante. Assim, o número de maneiras da torre chegar no quadrado da extrema direita em exatamente 7 jogadas é igual ao número de maneiras de colocar 6 divisórias entre as bolas na fileira. Qualquer divisória pode ser colocada em qualquer um dos 10 espaços entre as 11 bolas e duas divisórias não podem ficar num mesmo espaço (pois duas divisórias num mesmo espaço não correspondem a uma jogada). Logo, a resposta é 210.

TRÊS HOMENS EM CONFLITO

No primeiro momento devem embarcar os mais leves ou seja os de 60 kg e 65 kg (total = 125 kg).
Logo em seguida um desses homens deve voltar a margem de origem. Sai do barco e deixa o homem de 80 kg embarcar e atravessar sozinho para a margem 2. O outro homem mais leve então pega o barco e retorna para pegar o outro mais leve. No final voltam os dois novamente juntos.

Uma Conta de Matemática Difícil de Resolver

Isso é tudo menos um problema de matemática financeira e, na realidade, somos induzido ao erro pelo narrador, então vamos ao segredo:

O gerente do bar recebeu R$ 30,00 e deu o troco de R$ 5,00 ao garçom para que este o devolvesse aos homens. Logo, então o gerente ficou com R$ 25,00. O garçom devolveu R$ 3,00 aos homens, ficando com R$ 2,00.

Mas o que está sendo dito erradamente é que os homens pagaram R$ 27,00, ao invés dos R$ 25,00,

Temos no cálculo real:

R$ 25,00 que o gerente recebeu +

R$ 3,00 que o garçom devolveu +

R$ 2,00 que ficaram com o garçom

Total R$ 30,00 iniciais.

O desaparecimento de R$ 1,00 é porque o garçom ficou com R$ 2,00,e esse valor não foi contabilizado  pelos homens. Dessa forma fomos levados a pensar que  eles teriam pago R$ 27,00 e não R$ 25,00, valor real pago.

Lendo um Livro

supondo x o número de páginas do livro, então:

x/5 = x/3 -16

x/5 – x/3 = -16

(3x – 5x)/15 = -16

3x – 5x = -16*15

-2x = -240

x = 120

Contando Quadrados

11 quadrados.

Precisamente, há:

• 5 quadrados 1×1;
• 5 quadrados 2×2;
• 1 quadrado 3×3.

Contando Quadrados – Parte 2

30 Quardados

• 16 quadrados unitários
• 9 quadrados 2×2
• 4 quadrados 3×3
• 1 quadrado 4×4

Contando Triângulos Mágicos

São 38 triângulos = 24 Triângulos Básicos + 12 Triângulos compostos por quatro triângulos básicos + 2 Triângulos compostos por 9 triângulos básicos.

Enigmas Matemáticos com Figuras

Como ADBO é um retângulo temos que AB = OD. Mas OD é um raio, cujo comprimento também é igual ao comprimento de OC, que por sua vez é igual a OB + BC = 4 + 2 = 6 cm

Dividindo o Bolo

Pinturas na Parede

Observe que o número da pintura é exatamente o ângulo entre o ponteiro das horas e o ponteiro dos minutos, quando este último se desloca no sentido anti-horário até sobrepor-se ao ponteiro das horas.

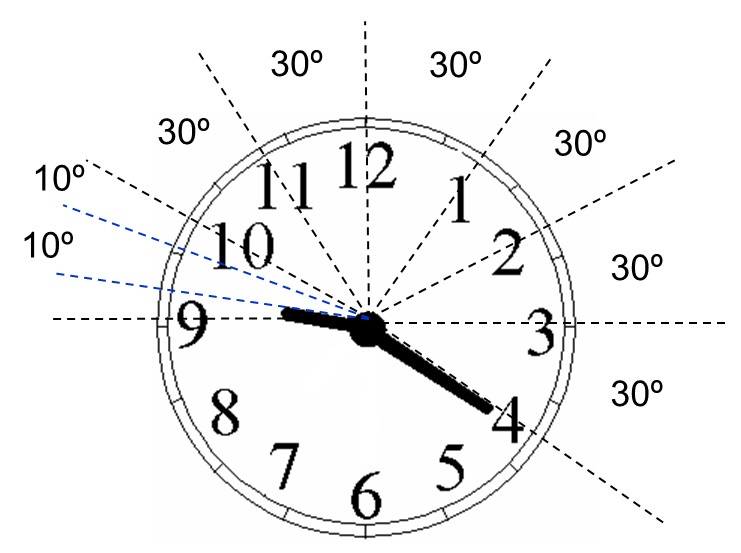
Assim: 6 x 30º + 10º + 10º = 200º. Às 21h 20min o artista pendurará a obra “número 200”.

Um Vidro Cheio de Bactérias

Como a quantidade de bactérias sempre dobra a cada segundo, no segundo anterior ao vidro encher ele deveria estar completo pela metade. Logo, o vidro estava com bactérias até a metade no segundo 59.

Você pode encontrar esta mesma solução matematicamente observando que no segundo s, temos 2^{s}k bactérias no vidro, se k é a quantidade inicial de bactérias. Desta forma, 2^{60}k é quantidade de bactérias que encheria o vidro. Dividindo esta quantidade por 2, ou seja, a metade do vidro, encontraríamos exatamente 2^{59}k . Portanto, o vidro estava com bactérias pela metade aos 59 segundos.

Leia Mais:

• Problemas do Milênio | Os 7 Problemas de Matemática para o Século XXI
• Gráficos | Da Análise Estatística ao Mercado de Ações
• Matemática Financeira Usando a HP-12C
• Ajuste de Dados – Como fazer arredondamento de números?
• Efeito Borboleta | Edward Lorenz e a Teoria do Caos
• Corda Vibrante | A Equação da Onda Unidimensional