Transformada de Fourier | 1ª Lista de Exercícios Resolvidos

Neste artigo queremos apresentar uma lista de exercícios resolvidos sobre a Transformada de Fourier, que é uma transformada integral que expressa uma função em termos de funções de base sinusoidal.

A Transformada de Fourier de uma função f(x) é definida pela integral $$\mathscr{F}\{ f(x) \} = \int\limits^{\infty}_{-\infty}{f(x)e^{-i\alpha x}dx} = F(\alpha)$$ e sua Transformada Inversa de Fourier é dada por $$\mathscr{F}^{-1}\{ F(\alpha) \} = \frac{1}{2\pi}\int\limits^{\infty}_{-\infty}{F(\alpha)e^{i\alpha x}d\alpha} = f(x).$$ As constantes 1 e \dfrac{1}{2 \pi} que precedem as integrais da definição da Transformada de Fourier poderiam ser substituídas por quaisquer outras constantes cujo produto fosse \dfrac{1}{2 \pi} .

Transformada de Fourier | 1ª Lista de Exercícios Resolvidos

1) Usando a Transformada de Fourier da derivada, determine a transformada de f(x) = e^{-x^2/2}.

SOLUÇÃO: Da propriedade da Transformada de Fourier da derivada temos que, $$\mathscr{F}\{f'(x)\} = -i\alpha F(\alpha) \Leftrightarrow \mathscr{F}\{-xe^{-x^2/2}\} = -i\alpha \mathscr{F}\{e^{-x^2/2}\}.$$ Usando a Tabela de Transformada de Fourier encontramos $$ \mathscr{F}\{-xe^{-x^2/2}\} = -\frac{\sqrt{ \pi }}{4} \alpha e^{-\alpha^2 /4}.$$

Logo, $$-\frac{\sqrt{ \pi }}{4} \alpha e^{-\alpha^2 /4} = -i\alpha \mathscr{F}\{e^{-x^2/2}\} .$$ Portanto, $$\mathscr{F}\{e^{-x^2/2}\} = \frac{\sqrt{ \pi }}{4i} e^{-\alpha^2 /4} .$$

2) (a) Ache a Transformada de Fourier, F ( \alpha ) , de $$f(x) = \left\{ \begin{array}{ll}
1; & |x|<a,\\
0; & |x|>a.
\end{array}
\right.$$

SOLUÇÃO: A transformada de Fourier desta função é dada por $$F(\alpha) = \int\limits_{- infty}^{+\infty}{f(u)e^{-i \alpha u} du} = \int\limits_{- a}^{+a}{e^{-i \alpha u} du} = \frac{2 sen(\alpha a)}{\alpha}; \;\; a \neq 0.$$

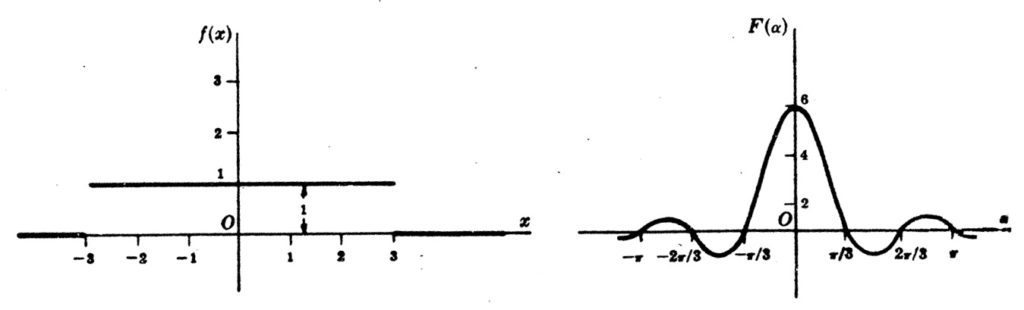
(b) Esboce os gráficos de f(x) e F ( \alpha ) para a=3.

SOLUÇÃO: 

(c) Use o resultado do item (a) para calcular $$ \int \limits_{- \infty}^{ \infty}{\frac{sen (\alpha a ) cos ( \alpha x )}{\alpha} d \alpha}$$

SOLUÇÃO: Pela transformada de Fourier Inversa obtemos $$f(x) = \frac{1}{2 \pi}\int\limits_{- \infty}^{+ \infty}{F( \alpha) e^{i \alpha x}d \alpha},$$ e pela relação com a Integral de Fourier obtemos $$ \frac{1}{2 \pi}\int\limits_{- \infty}^{+ \infty}{ \frac{2 sen(\alpha a)}{\alpha} e^{i \alpha x}d \alpha} = \left\{ \begin{array}{ll} 1; & |x|<a,\\ 1/2; |x| = a \\ 0; & |x|>a. \end{array} \right.$$

O lado esquerdo da equação pode ser escrito, usando a fórmula e^{i \alpha x} = \cos{\alpha x} + i \sin{\alpha x} , como $$ \frac{1}{\pi}\int\limits_{- \infty}^{+ \infty}{ \frac{sen(\alpha a) \cos{\alpha x}}{a} d \alpha} + \frac{i}{ \pi}\int\limits_{- \infty}^{+ \infty}{ \frac{sen(\alpha a) sen{\alpha x}}{a} d \alpha}.$$ Observe que o integrando na segunda integral é ímpar, de modo que a integral é zero. Então, podemos afirmar que $$ \frac{1}{2 \pi}\int\limits_{- \infty}^{+ \infty}{ \frac{2 sen(\alpha a)}{\alpha} e^{i \alpha x}d \alpha} = \frac{1}{\pi}\int\limits_{- \infty}^{+ \infty}{ \frac{sen(\alpha a) \cos{\alpha x}}{\alpha} d \alpha}. $$ Portanto, $$ \frac{1}{\pi}\int\limits_{- \infty}^{+ \infty}{ \frac{sen(\alpha a) \cos{\alpha x}}{\alpha} d \alpha} = \left\{ \begin{array}{ll} 1; & |x|<a,\\ 1/2; & |x| = a \\ 0; & |x|>a. \end{array} \right.$$

(d) Deduza o valor de $$ \int \limits_{0}^{ \infty}{\frac{sen ( u ) }{u} d u}$$

SOLUÇÃO: Se x = 0 e a = 1 no resultado do item anterior, temos que $$\int\limits_{- \infty}^{+ \infty}{ \frac{sen(\alpha a)}{\alpha} d \alpha} = \pi \Leftrightarrow \int\limits_{- \infty}^{+ \infty}{ \frac{sen(\alpha a)}{\alpha} d \alpha} = \frac{\pi}{2},$$ pois o integrando é par.

3) (Equação do calor numa haste infinita) Resolva, usando a transformada de Fourier, a equação $$k\frac{\partial ^2 u}{\partial x^2} = \frac{\partial u}{\partial t},\;\;\;\;\; -\infty < x < \infty, \;\;\;\;\;t>0,$$ sujeita a $$u(x,0) =f(x)$$

O problema acima é o da determinação da temperatura em uma barra delgada infinita cuja superfície é isolada e cuja temperatura inicial é f(x) .

SOLUÇÃO: Tomando a transformada de Fourier em relação a x de ambos os membros da equação diferencial parcial dada, temos, por processos similares ao aos exemplos deste artigo, $$ \frac{d}{dt} \mathscr{F}(u) = -k \lambda ^2 \mathscr{F}(u) $$ onde escrevemos a derivada total pois \mathscr{F}(u) depende apenas de t e não de x . Resolvendo a equação diferencial ordinária dada pela equação anterior possui solução dada por $$ \mathscr{F}(u) = C e^{-k \alpha ^2 t}$$ ou mais explicitamente $$ \mathscr{F} \left\{ u(x,t) \right\} = C e^{-k \alpha ^2 t}.$$ Fazendo t = 0 nesta solução, vemos que $$ \mathscr{F} \left\{ u(x,0) \right\} = C = f(x)$$ de modo que obtemos $$ \mathscr{F}(u) = \mathscr{F} \left\{ f \right\}  e^{-k \alpha ^2 t}.$$

Usando a convolução para a Transformada de Fourier, podemos encontrar $$ u(x,t) = f(x) * \mathscr{F}^{-1} \left\{ e^{-k \alpha ^2 t} \right\} .$$

Como, pela tabela de Transformadas de Fourier, $$ \mathscr{F}^{-1} \left\{ e^{-k \alpha ^2 t} \right\}  = \sqrt{\frac{1}{4 \pi k t}} e^{-x^2/4kt}, $$ então, $$ u(x,t) = f(x) * \sqrt{\frac{1}{4 \pi k t}} e^{-x^2/4kt} = \int\limits_{- \infty}^{\infty}{f(w)\sqrt{\frac{1}{4 \pi k t}} e^{-(x-w)^2/4kt} dw}.$$ Usando a mudança de variável z^2 = \dfrac{(x-w)^2}{4kt} \Leftrightarrow z = \dfrac{(x-w)}{2 \sqrt{kt}} , o que nos leva a $$u(x,t) = \frac{1}{ \sqrt{ \pi}} \int\limits_{- \infty}^{\infty}{e^{z^2} f(x-2z \sqrt{kt})dz}.$$

Leia Mais:

• Corda Vibrante | A Equação da Onda Unidimensional
• Séries de Fourier | História, Definição e Condições de Existência.
• Solucionando EDO’s por Transformada de Laplace | Exercícios Resolvidos
• A Integral de Fourier

Assista Nossa Vídeo-Aula Sobre Transformadas de Fourier:

https://www.youtube.com/watch?v=q11XX_7jaxw