O Teorema de Pitágoras é um dos resultados mais importantes da matemática e uma de suas bases fundamentais, colecionando inúmeras e diferentes demonstrações desde o século V a.C., quando foi proposto. Em seu texto “Teorema de Pitágoras e Áreas”, que foi uma de nossas fontes para este artigo, Eduardo Wagner conta que “em 1940, o matemático americano E. S. Loomis publicou 370 demonstrações deste teorema”.
O enunciado do Teorema de Pitágoras nos diz que: “Em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa é igual à soma das áreas dos quadrados que têm como lados cada um dos catetos.” Ou seja, se a é a medida da hipotenusa e b e c são as medidas dos catetos, este enunciado é equivalente à equação $$ a^2 = b^2 + c^2.$$
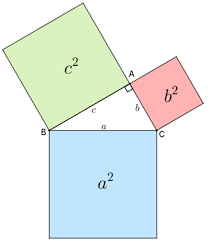 O Teorema de Pitágoras afirma que a área em azul é igual à soma das areas verde e vermelha
O Teorema de Pitágoras afirma que a área em azul é igual à soma das areas verde e vermelha
Quem Foi Pitágoras?
Pitágoras (569 – 480 a.C.) foi um dos maiores expoentes do pensamento grego, nascido na ilha de Samos, e que junto com Tales (que havia nascido em Mileto 50 anos antes) estabeleceu as bases para o pensamento matemático moderno. Personagem intrigante, Pitágoras acumula lendas em torno de seu nome, que o liga a sociedades secretas modernas como a própria Maçonaria.
O que se sabe de fato é que Pitágoras bebeu da fonte de todo o conhecimentos disponível em sua época, viajando por Egito, Babilônia e Índia, absorvendo as ideias filosóficas e matemáticas de cada um destes locais. Tanto que ao voltar à Grécia Antiga, fundou uma escola iniciática em Crotona dedicada ao estudo da filosofia e da matemática
Foi Realmente Pitágoras o Descobridor do Teorema?
Infelizmente não é possível responder esta pergunta com total certeza, pois todos os documentos da época se perderam e o que se sabe vem de referências de outros autores que viveram séculos depois. Além disso, a escola que ele gerenciava era colaborativa, ou seja, todo o conhecimento e todas as descobertas eram comuns, pertenciam a todos.
Assim, não podemos garantir nem se foi Pitágoras ou algum de seus alunos que demonstrou o Teorema que leva seu nome, pois era também habitual que o mestre levasse todo o crédito pela descoberta do aluno.
Além disso, existes provas irrefutáveis de que os babilônios conheciam o Teorema de Pitágoras desde por volta de 1800 a 1600 a.C., ao menos a relação entre os lados do triângulo retângulo. Entretanto, não há, como é de se esperar, vestígios de alguma demonstração desta relação. Lembremos que este não era o objetivo da matemática no período.
Duas Demonstrações do Teorema de Pitágoras
Os problemas com os registros históricos nos impedem de garantir qualquer foi a demonstração inicial do Teorema de Pitágoras, mas especula-se que foi usada primeiramente uma abordagem com áreas. Abaixo apresento as duas demonstrações mais conhecidas deste teorema: a clássica, possivelmente desenvolvida pelos pitagóricos, e uma por semelhança de triângulos.
Além destas duas demonstrações, existe uma outra ainda mais elegante, publicada em 1873 por Henry Preigal, um livreiro de Londres, que usa apenas elementos básicos da geometria em seu argumento. “Trata-se da forma mais evidente de mostrar que a soma das áreas dos quadradas construídos sobre os catetos preenchem o quadrado construído sobre a Hipotenusa” escreveu Eduardo Wagner em “Teorema de Pitágoras e Áreas”.
Ele continua, ao expor o raciocínio da demonstração de Perigal para o Teorema de Pitágoras: “Perigal corta o quadrado construído sobre o maior cateto por duas retas passando pelo seu centro, uma paralela à hipotenusa do triângulo e outra perpendicular, dividindo esse quadrado em quatro partes congruentes. Essas quatro partes e mais o quadrado construído sobre o menor cateto, preenchem completamente o quadrado construído sobre a hipotenusa”.
1) A DEMONSTRAÇÃO CLÁSSICA DO TEOREMA DE PITÁGORAS
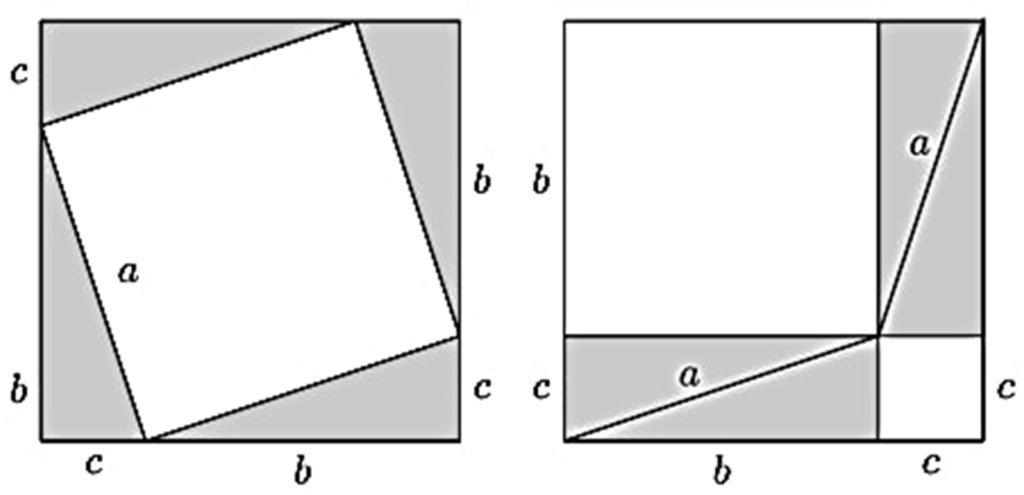
Considerando a como a medida da hipotenusa e b e c as medidas dos catetos, tome o quadrado cujo lado é b +c conforme a a figura abaixo, onde retiramos do quadrado de lado b +c quatro triângulos iguais ao triângulo retângulo dado, restando um quadrado de lado a .
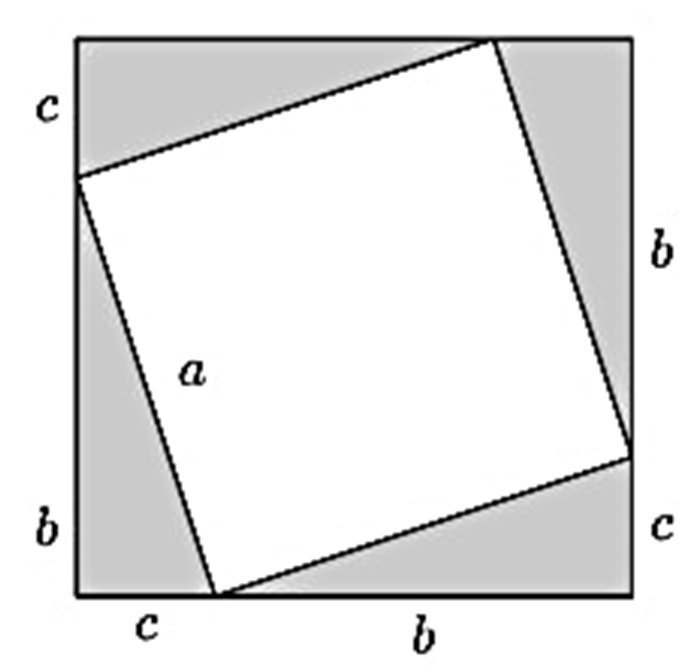
Agora, retiramos do quadrado de lado b +c os quatro triângulo iguais ao triângulo retângulo dado, restando um quadrado de lado b e um quadrado de lado c , como vemos na figura abaixo:
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Portanto, a área do quadrado de lado a é igual à soma das áreas dos quadrados cujos lados medem b e c .
2) A DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS POR SEMELHANÇAS
Considere um triângulo ABC, retângulo em Â, onde traçamos a altura AH. Podemos mostrar que os triângulos AHB e AHC são semelhantes ao triângulo ABC. De fato, pela figura abaixo, podemos mostrar que como a_1 + b_1 = 90º pela soma dos ângulos internos de um triângulo e a_1 + a_2 = 90º podemos concluir que a_1 = b_2 e a_2 = b_1 . Desta forma, os três triângulos são semelhantes pela congruência entre os ângulos.
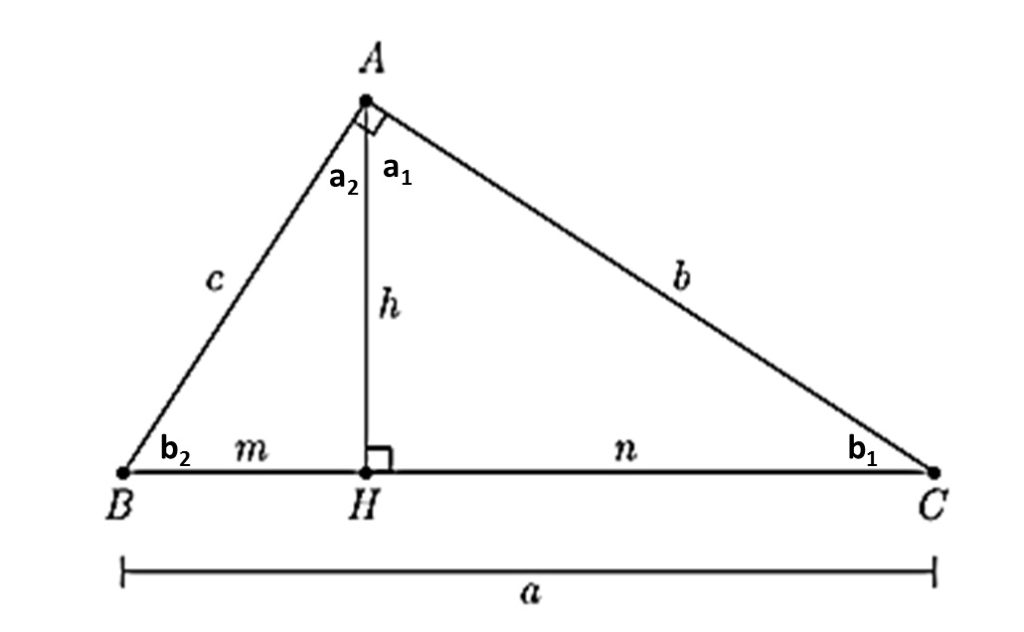 Desta semelhança dos triângulos AHB e ABC, temos que c^2 = am e, da semelhança dos triângulos AHC e ABC, temos que b^2 = a n . Somando essas duas relações membro a membro, encontramos $$ b^2 + c^2 = am + an = a \times a = a^2 .$$
Desta semelhança dos triângulos AHB e ABC, temos que c^2 = am e, da semelhança dos triângulos AHC e ABC, temos que b^2 = a n . Somando essas duas relações membro a membro, encontramos $$ b^2 + c^2 = am + an = a \times a = a^2 .$$
A Recíproca do Teorema de Pitágoras
Uma pergunta imediata sobre o Teorema de Pitágoras é sobre a recíproca: Todo triângulo com medidas de lado a, b, \text{ e } c, tais que a^2 = b^2 + c^2 , é retângulo? A resposta é sim, mas não iremos demonstrar esta recíproca neste artigo.
Os Ternos Pitagóricos
Leia Mais:
- O que são Números Irracionais? Definição, História e Propriedades
- Funções Trigonométricas (Seno, Cosseno, Tangente…) | Pré-Cálculo
- Análise Combinatória | Resumo de Fórmulas e Exercícios Resolvidos
- Números Racionais | Definição, Propriedades e Operações Elementares

