Série de Fourier | 3ª Lista de Exercícios Resolvidos

Neste artigo apresentamos uma terceira lista de exercícios resolvidos sobre a Série de Fourier, que são largamente utilizadas na resolução de muitos problemas de valores de contorno.

As condições de Dirichlet nos diz que supondo f(x) definida, exceto possivelmente em um número finito de de pontos do intervalo (-L,L), periódica de período 2L, sendo f(x) e f'(x) seccionalmente contínuas em (-L,L), então a série de Fourier $$\frac{1}{2} a_0 + \sum\limits_{n=1}^{\infty}\left( a_n \cos{\left( \frac{n\pi x}{L} \right)}+b_n \sin{\left( \frac{n\pi x}{L} \right)} \right)$$ com coeficientes dados por $$a_n = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \cos{\left( \frac{n\pi x}{L} \right)} dx} $$ e $$b_n = \frac{1}{L}\int\limits _{-L}^{L}{f(x) \sin{\left( \frac{m\pi x}{L} \right)} dx}$$ converge para f(x) se x é ponto de continuidade; \frac{f(x+0) + f(x-0) }{2} se x é ponto de descontinuidade, sendo f(x+0) o limite de f(x) à direita de x e f(x-0) o limite de f(x) à esquerda de x.

Séries de Fourier | 3ª Lista de Exercícios Resolvidos

1) Desenvolva as funções abaixo em Séries de Fourier:

a) f(x) = x; se -2 <x <2.

SOLUÇÃO: Esta função é ímpar, logo a_0 = a_n = 0 . Portanto sua expansão em série de Fourier será dada por $$f(x) = \sum\limits_{n=1}^{\infty}{b_n \text{sen}{\left( \frac{n \pi}{2} x \right)}},$$ onde $$b_n = \frac{2}{2}\int\limits_{0}^{2}{f(x) \text{sen}{\left( \frac{n \pi}{2} x \right)} dx} = \int\limits_{0}^{2}{f(x) \text{sen}{\left( \frac{n \pi}{2} x \right)} dx}$$

Por integração por partes encontramos que $$b_n = \frac{4 (-1)^{n+1}}{n \pi}$$ portanto, $$f(x) = \sum\limits_{n=1}^{\infty}{ \frac{4 (-1)^{n+1}}{n \pi} \text{sen}{\left( \frac{n \pi}{2} x \right)}}$$

b) f(x) = 0, se - \pi < x <0 , e f(x) = \pi - x se 0<x< \pi .

SOLUÇÃO: Neste caso, L = \pi , logo, nossa função será expandida em série de Fourier como $$ f(x) = \frac{ a_0}{2} + \sum\limits_{n=1}^{\infty}{ \left[ a_n \text{cos}{\left( n x \right)}+ b_n \text{sen}{\left( n x \right)} \right]},$$ onde $$a_0 = \frac{1}{ \pi } \int\limits_{- \pi}^{\pi}{f(x)dx} = \frac{1}{ \pi } \int\limits_{0}^{\pi}{[\pi – x]dx} = \frac{\pi}{2}$$ e usando integração por partes encontramos $$ a_n = \frac{1}{ \pi } \int\limits_{- \pi}^{\pi}{f(x) cos(nx)dx} = \frac{1}{ \pi } \int\limits_{0}^{\pi}{[\pi – x]cos(nx)dx} = \frac{1-cos(n \pi)}{\pi n^2} = \frac{1-(-1)^n }{\pi n^2} $$ $$ b_n = \frac{1}{ \pi } \int\limits_{- \pi}^{\pi}{f(x) sen(nx)dx} = \frac{1}{ \pi } \int\limits_{0}^{\pi}{[\pi – x]sen(nx)dx} = \frac{1}{n} .$$

Portanto, $$ f(x) = \frac{ \pi}{4} + \sum\limits_{n=1}^{\infty}{ \left[\frac{1-(-1)^n }{\pi n^2} \text{cos}{\left( n x \right)}+ \frac{1}{n} \text{sen}{\left( n x \right)} \right]},$$

c) f(x) = -1 , se - \pi < x <0 , e f(x) = 1 se 0 \leq x < \pi .

SOLUÇÃO: Esta função é chamada de onda retangular e basta um esboço de seu gráfico para perceber que ela ímpar, logo a_0 = a_n = 0 . Portanto sua expansão em série de Fourier será dada por $$f(x) = \sum\limits_{n=1}^{\infty}{b_n \text{sen}{\left( nx \right)}},$$ onde $$b_n = \frac{2}{\pi}\int\limits_{0}^{\pi}{f(x) \text{sen}(nx) dx} = \frac{2}{\pi}\int\limits_{0}^{\pi}{1 \text{sen}(nx) dx} = \\ = \frac{2}{n \pi} \left[ (-1)^{n+1} +1 \right].$$ Desta forma, obtemos que $$ b_{2n} = 0 \qquad \text{e} \qquad b_{2n-1} = \frac{4}{(2n-1) \pi}$$ Portanto, $$f(x) = \sum\limits_{n=1}^{\infty}{\frac{4}{(2n-1) \pi} \text{sen}{\left( [2n-1]x \right)}}$$

d) f(x) = | sen(x) | se x \in [ \pi , \pi ] .

SOLUÇÃO: Um esboço do gráfico desta função nos mostra que ela é par:

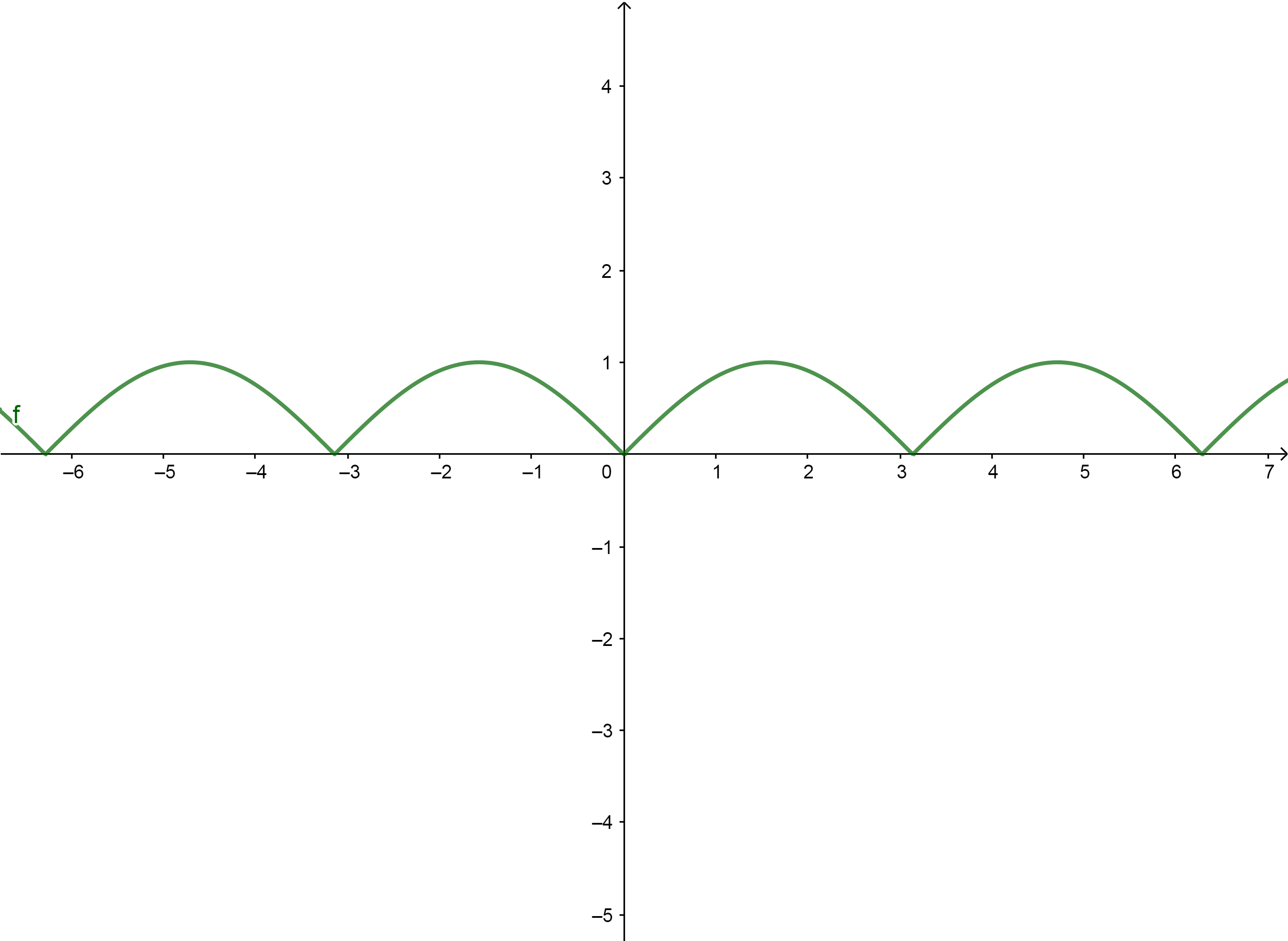
Logo, b_n = 0 . Assim, nossa função será expandida em série de Fourier como $$ f(x) = \frac{a_0}{2}+\sum\limits_{n=1}^{+ \infty}{a_n \text{cos}\left( n x \right) }$$ onde $$ a_0 = \frac{2}{ \pi} \int\limits_{0}^{ \pi }{sen(x) dx} = \frac{4}{\pi}$$ $$a_n = \frac{2}{ \pi} \int\limits_{0}^{ \pi }{sen(x) cos (nx) dx} = \\ =\frac{1}{\pi} \int\limits_{0}^{ \pi }{\left[ sen([n+1]x) – sen([n-1] x) \right] dx} = \\ = \frac{1}{ \pi} \left[ \frac{1}{n+1} (1-cos([n+1] \pi) ) – \frac{1}{n-1} (1-cos([n-1] \pi) ) \right] = \\ = \left\{ \begin{array}{lll} 0 & ; & \text{ se n é ímpar}\\ \frac{-4}{(n^2 -1) \pi}& ; & \text{ se n é par} \end{array} \right.$$

Assim, $$ a_{2n} = \frac{-4}{([2n]^2 -1) \pi} \qquad \text{e} \qquad a_{2n-1} = 0 $$ Portanto, $$ f(x) = \frac{2}{\pi}+\sum\limits_{n=1}^{+ \infty}{ \frac{-4}{(4n^2 -1) \pi} \text{cos}\left( 2n x \right) }$$

e) f(x) = |x|; \qquad -1 < x <1 .

SOLUÇÃO: Aqui, L = 1 . Como f é uma função par, b_n = 0 e $$ a_0 =  2 \int\limits_{0}^{1}{xdx} = 1 $$ $$ a_n = 2 \int\limits_{0}^{1}{x \text{cos} (n \pi x )dx} = \frac{2}{\pi ^2 n^2} \left( \text{cos} (n \pi  ) – 1 \right) = \frac{2}{\pi ^2 n^2} \left( (-1)^n – 1 \right).$$ Portanto, $$f(x) = \frac{1}{2} – \frac{4}{ \pi ^2 }\sum\limits_{ n =1 }^{ + \infty}{\frac{\text{cos} ([2n-1] \pi x)}{(2n-1)^2} }.$$

Exercícios Resolvidos sobre Séries de Fourier

• Séries de Fourier | 1ª Lista de Exercícios Resolvidos
• Séries de Fourier | 2ª Lista de Exercícios Resolvidos

Leia Mais:

• Séries de Fourier | História, Definição e Condições de Convergência.
• Séries de Fourier | Ortogonalidade das Funções Seno e Cosseno
• O Que São Funções Periódicas? Definição e Exemplos.
• Séries de Fourier | Os Coeficientes de Fourier
• Séries de Fourier de Senos e Cossenos | A Expansão em Meio-Intervalo.

Assista Nossa Vídeo-Aula Sobre Séries de Fourier: