Números Complexos | A Forma Polar e as Operações Elementares

Neste artigo queremos falar sobre a forma polar, ou trigonométrica, dos números complexos. Um número complexo z é um par ordenado (x,y) de número reais x e y onde se escreve $$z=(x,y)$$ e denominamos x de parte real e y de parte imaginária de z e escrevemos $$x=Re(z)\;\;\;e\;\;\;y=Im(z).$$

Dois números complexos são iguais se, e somente se, suas partes real e imaginária são iguais. Assim, (1,0) = (1,0), mas (1,0) \neq (0,1). O ponto (0,1) é denominado unidade imaginária e é denotado por i. Ou seja, $$i=(0,1).$$ Desta forma, (0,y) = y (0,1) = yi. De maneira análoga, podemos encarar (x,0) = x.

Assim, $$(x,y) = (x,0)+(0,y) = x(1,0) + y(0,1) = x+iy.$$ Na prática, um número complexo z=(x,y) é representado na forma $$z=x+iy=Re(z)+Im(z) i$$ que é denominada forma cartesiana de z. Se Re(z) = 0, então z é chamado de imaginário puro. O conjugado de um número complexo z=x+yi é denotado por \bar{z} e é dado por $$\bar{z} = x-yi.$$

A Forma Polar de Um Número Complexo

Em alguns problemas, a forma cartesiana de um numero complexo não é tão prática. Sendo assim, utilizamos uma transformação para os termos x e y da seguinte forma: $$x=r\cos{\theta}$$ e $$y=r\sin{\theta}$$ onde, $$|z| = r = \sqrt{x^2 + y^2} = \sqrt{z\bar{z}}$$ sendo r denominado valor absoluto, ou módulo de z e $$\theta = \arctan{\frac{y}{x}};\;\;\;\;- \pi < \theta \leq \pi$$ que é denominado argumento de z.

Desta forma, $$z=x+iy = r\left( cos(\theta) + i sen(\theta) \right).$$ Esta é chamada de forma trigonométrica ou polar de um número complexo  z , onde o números reais r e \theta são as coordenadas polares do ponto P(x,y) do plano.

O Argumento de um Número Complexo

Um argumento de um número complexo z \neq 0 , z = x + y i , é, por definição, qualquer dos ângulos \theta = \text{arg}(z) que o vetor \vec{OP} forma com o semi-eixo positivo dos x (como podemos ver na figura anterior).

É claro que todo número complexo não-nulo tem um infinidade de argumentos, dois quaisquer deles diferindo entre si por um múltiplo de 2 \pi . O argumento que pertence ao intervalo ( - \pi , \pi ] é chamado de argumento principal e é representado por \text{Arg}(z) .

Se \theta é um argumento de z = x + i y então $$ x = r \text{cos}( \theta ) \qquad \text{e} \qquad y = r \text{sen}( \theta ) .$$ Para z=0, nao existe o argumento de z.

Podemos garantir que $$ \text{ arg }(z_1 \cdot z_2 ) = \text{ arg }(z_1 ) + \text{ arg } (z_2 ) $$ $$\text{ arg } \left( \frac{ z_1 }{ z_2 } \right) =  \text{ arg }(z_1 ) – \text{ arg } (z_2 ) .$$

O Módulo de um Número Complexo

Geometricamente, |z| representa a distância de z à origem. Analogamente, |z-z_1| representa a distância entre z e z_1. O módulo de um número complexo z satisfaz as seguintes propriedades abaixo. Sejam z_1 e z_2 dois números complexos:

1. |z_1 z_2| = |z_1||z_2|
2. \left| \dfrac{z_1 }{ z_2} \right| = \dfrac{ |z_1| }{ |z_2| }
3. |z_1 + z_2| \leq |z_1| + |z_2| (Desigualdade Triangular)
4. |z_1 z_1| \geq 0 e |z_1 z_1| = 0 \Leftrightarrow z_1 =0

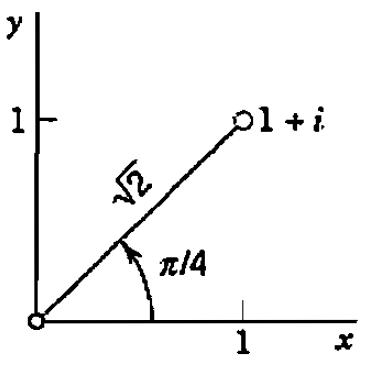
EXEMPLO 1: Considere o complexo z=1 + i.

1.  O módulo de z é \sqrt{2};
2.  o argumento de z é \frac{\pi}{4};
3.  a forma polar de z é \sqrt{2}\left( cos(\pi /4 ) + i sen(\pi /4 ) \right).
4.  a representação gráfica polar z

EXEMPLO 2: O número complexo z = 3 i é representado pelo ponto (0,3) , ou seja, pelo ponto 3 sobre o eixo dos y. Portanto, |z| = 3 e um dos argumentos de z é \dfrac{ \pi }{2} . Portanto, a forma trigonométrica de z é $$ z = 3 \left[ \text{cos} \left( \frac{\pi}{2} \right) + i \text{sen} \left( \frac{\pi}{2}  \right) \right].$$

Operações Algébricas Envolvendo a Forma Polar

Podemos definir uma regra muito conveniente para a multiplicação de dois números complexos utilizando suas formas polares.

Sejam z_1 = r_1(\cos{\theta _1} + i \sin{\theta _1}) e z_2 = r_2 (\cos{\theta _2} + i\sin{\theta _2}) então $$z_1 . z_2 = r_1 r_2 \left[ \cos{(\theta _1 + \theta _2)} + i \sin{(\theta _1 + \theta _2)} \right]$$ e para a divisão $$\frac{z_1}{z_2} = \frac{r_1}{ r_2} \left[ \cos{(\theta _1 – \theta _2)} + i \sin{(\theta _1 – \theta _2)} \right].$$

Da fórmula para a multiplicação, provêm a fórmula de potenciação $$z^n = r^n \left( \cos{n \theta} + i \sin{n \theta} \right).$$ Se z=w^n, sendo w um número complexo, daí, $$w = \sqrt[n]{z} = \sqrt[n]{r} \left( \cos{\left( \frac{\theta +2k \pi}{n} \right)} + i \sin{\left( \frac{\theta +2k \pi}{n} \right)} \right).$$

Observe que as raízes de um número complexo tem todas o mesmo módulo \sqrt[n]{r} . Se r \neq 0 , as imagens dessas raízes se situam em uma circunferência de centro na origem e raio \sqrt[n]{r} como ilustrado na figura abaixo:

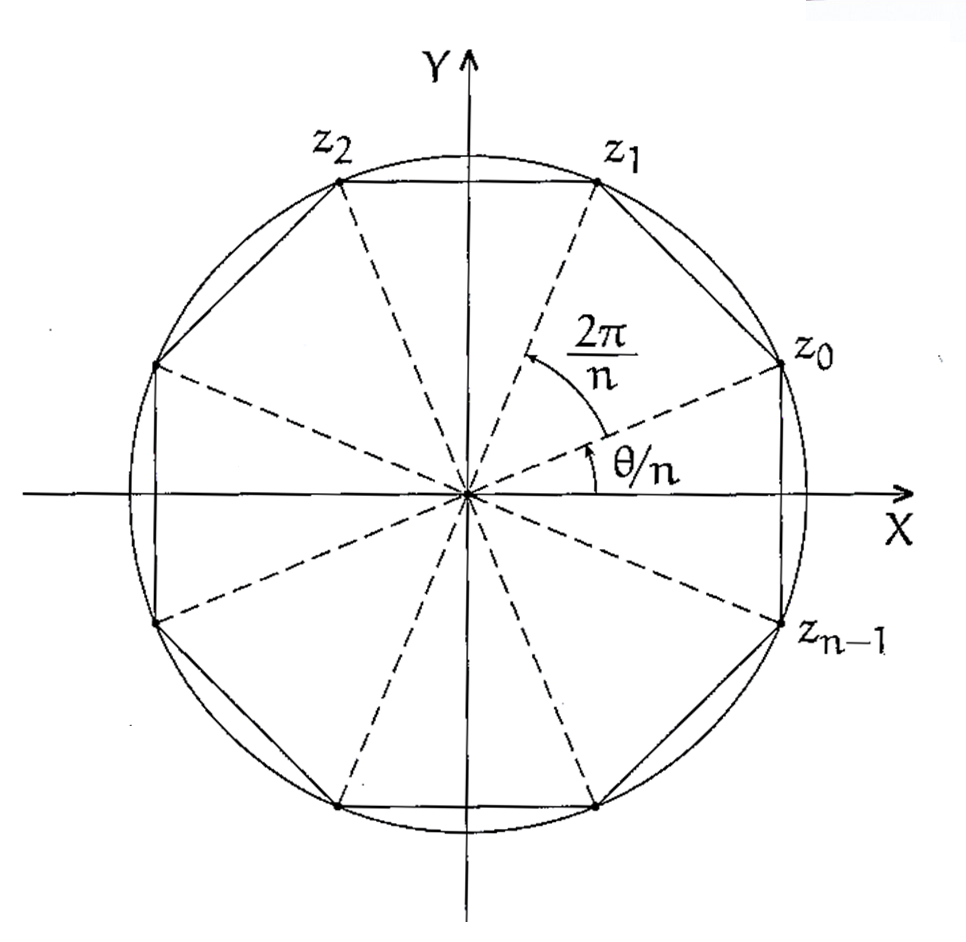
Observe ainda por esta figura que dando valores inteiros para k , os argumentos crescem em progressão aritmética de razão 2 \pi / n , o que nos mostra que as raízes estão uniformemente espaçadas na circunferência.

As Raízes Complexas da Unidade

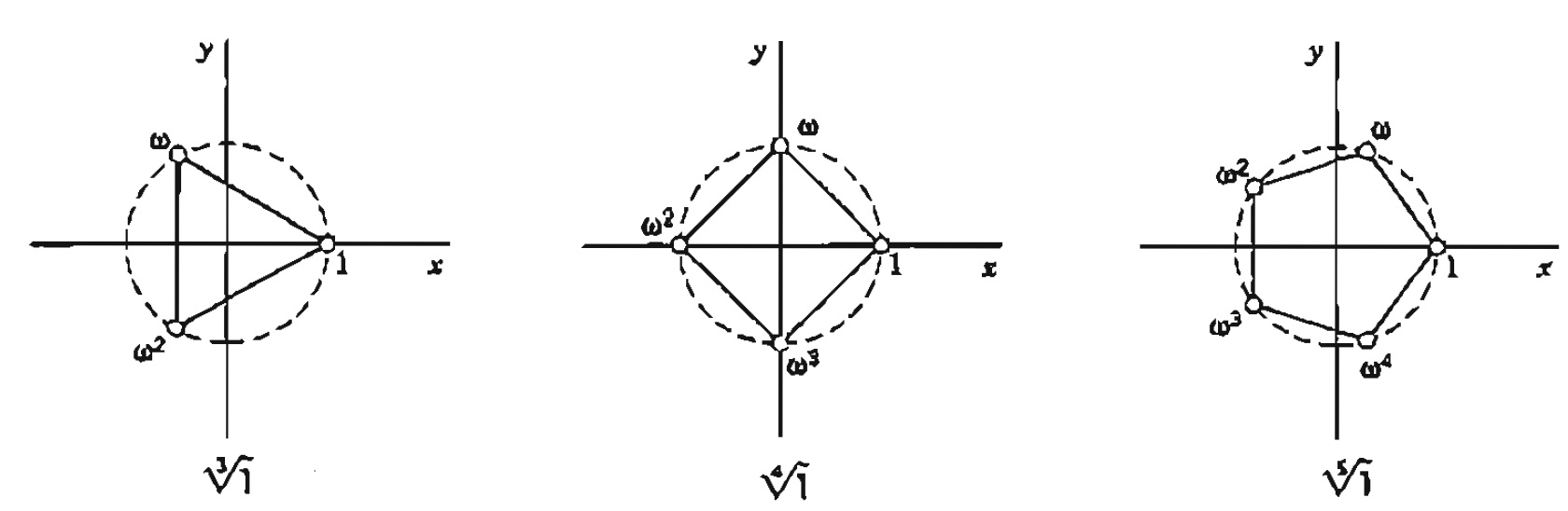
Considere z =1. Assim, $$z = \cos{0} + i \sin{0}$$, logo, $$\sqrt[n]{z} = \left( \cos{\left( \frac{2k \pi}{n} \right)} + i \sin{\left( \frac{2k \pi}{n} \right)} \right)$$ Observe que as raízes n-ésimas da unidade representadas no plano complexo são os vértices d e um polígono regular de n lados como mostra a figura abaixo:

A Fórmula de De Moivre

Abraham de Moivre (1667–1754) nasceu em Vitry-Vitry-le-François, França, e era amigo íntimo de Sir Isaac Newton , James Stirling e Edmond Halley. Um matemático apaixonado, de Moivre fez contribuições significativas para a geometria analítica, trigonometria e a teoria da probabilidade.

No entanto, ele é mais conhecido pela Lei de De Moivre (freqüentemente chamada de Fórmula de De Moivre) e pela Aproximação de Stirling. A fórmula da multiplicação de dois complexos escritos na forma polar estende-se para um número qualquer de fatores.

Considere $$z_j = r_j (\cos{\theta _j} + i \sin{\theta _j})\;\;\;\;\;j=1,2,3,4,…,n.$$ Daí o produto dos n fatores z_j é dado pela fórmula $$z_1 z_2 … z_n = r_1 r_2 … r_n \left( \cos{(\theta _1 + \theta _2 + … + \theta _n)} + i \sin{(\theta _1 + \theta _2 + … + \theta _n)} \right).$$

Em particular, quando todos os z_n = z são iguais e com módulo igual a 1, temos que z_n = z = (\cos{\theta} + i \sin{\theta}) e aí obtemos a conhecida Fórmula de Moivre $$z^n = (\cos{\theta} + i \sin{\theta})^n = (\cos{n\theta} + i \sin{n\theta})$$ que vale para qualquer n \in \mathbb{Z}.

Podemos generalizar a Fórmula de De Moivre da seguinte maneira (uma demonstração desta fórmula será feita na lista de exercícios linkada abaixo):

FÓRMULA DE De MOIVRE: Se n é inteiro, então $$ \left[ r (\cos{\theta} + i \sin{\theta}) \right]^n  = r^n (\cos{n \theta} + i \sin{ n \theta}) .$$

A Exponencial de um Número Complexo

Sabemos pelo artigo sobre expansão em Série de Potências que \begin{eqnarray*}
e^x & = & \sum_{n=0}^{\infty}{\frac{x^n}{n!}} = 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+…. \\
\cos{x} & = & \sum_{n=0}^{\infty}{\frac{(-1)^n x^{2n}}{(2n)!}} = 1- \frac{x^2}{2!}+\frac{x^4}{4!}-…. \\
\sin{x} & = & \sum_{n=0}^{\infty}{\frac{(-1)^n x^{2n+1}}{(2n+1)!}} = x- \frac{x^3}{3!}+\frac{x^5}{5!}-…. \end{eqnarray*}

Considere z=x+yi. Assim,

\begin{eqnarray*}
e^z & = & e^{x+yi} \\
& = & e^x e^{iy} \\
& = & e^x \left( \sum_{n=0}^{\infty}{\frac{(yi)^n}{n!}} \right) \\
& = & e^x \left( 1+yi+\frac{(yi)^2}{2!}+\frac{(yi)^3}{3!}+…. \right) \\
& = & e^x \left( 1+yi-\frac{(y)^2}{2!}-i\frac{(y)^3}{3!}+\frac{(y)^4}{4!} + i \frac{(y)^5}{5!}+…. \right) \\
& = & e^x \left( 1-\frac{y^2}{2!}+\frac{(y)^4}{4!} -\frac{y^6}{6!}…. \right) + e^x \left( y-\frac{y^3}{3!}+\frac{y^5}{5!} -\frac{y^7}{7!}…. \right)i\\
& = & e^x (\cos{y} + i \sin{y})
\end{eqnarray*}

EXEMPLO

Calcule exp{(3 + 7 \pi i)}.

Pela fórmula da exponencial $$exp{(3 + 7 \pi i)} = e^3 \left( \cos{7 \pi} + i \sin{7\pi} \right) = e^3 \left( -1 \right) = -e^3.$$

Propriedades da Exponencial de um Número Complexo

Da definição da exponencial complexa e^{z} que acabou de ser enunciada, e das propriedades das funções e^x, \sin{x} e \cos{x}, decorrem as seguintes propriedades da exponencial:

1. e^{z_1} e^{z_2} = e^{z_1 + z_2}
2. e^{-z} =\frac{1}{e^{z}}
3. \left( e^z \right)^n = e^{nz}; n inteiro.
4. e^z \neq 0, \forall z;
5. \left| e^{z} \right| = e^{Re(z)}
6. e^z = 1 \Leftrightarrow z= 2k\pi i, k inteiro.

OBSERVAÇÕES:

1. Se considerarmos z escrito a sua forma polar, então e^z assume sua forma compacta dada por $$e^z = r e^{i \theta}.$$
2. Muitas vezes, quando o expoente é muito carregado utilizamos a notação exp (z). Por exemplo, costuma-se escrever $$exp \left[\frac{z}{2} \left( t – \frac{1}{t}\right) \right]$$ em vez de $$e^{\frac{z}{2} \left( t – \frac{1}{t}\right)}.$$

Listas de Exercícios Resolvidos:

• A Forma Polar de Um Número Complexo | Lista de Exercícios Resolvidos
• Números Complexos: Módulo e Conjugado | Exercícios Resolvidos

Referências Bibliográficas:

Abaixo seguem os títulos usados como base para este artigo. Para conferir os títulos específicos basta clicar nos links em azul.

1. KREYSZIG, E. Advanced Engineering Mathematics, John Wiley & Song, Inc., 8th Edition, 1999.
2. ÁVILA, Geraldo S. S. Variáveis Complexas e Aplicações. 3ª Edição. Rio de Janeiro: LTC, 2000.
3. ZILL, Dennis G. “Curso Introdutório à Análise Complexa com Aplicações”. 2ª edição, LTC, Rio de Janeiro, 2011 
4. LIMA, Elon Lages, CARVALHO, Paulo Cezar Pinto, WAGNER, Eduardo e MORGADO, Augusto César. “A Matemática do Ensino Médio, volume 3”.

Leia Mais:

• Números Complexos | A Forma Polar e as Operações Elementares
• Números Complexos | A Exponencial de um Número Complexo
• Funções de Variáveis Complexas | Uma Introdução.
• O que são Conjuntos Numéricos? Dos Naturais aos Complexos.