Na história da matemática, o primeiro a utilizar os números complexos foi o matemático italiano Girolando Cardano por volta do século XVI para solucionar equações cúbicas. Porém, foi Gauss (1787 – 1855), o maior matemático de todos os tempos, quem apresentou uma teoria consistente para os números complexos.
Em 1545, Cardano (1501 – 1576), em seu livro “Ars Magna” (“A Grande Arte”), mostrou o método para resolver equações do terceiro grau que é hoje chamado de Fórmula de Cardano que recaia em raízes quadradas de números complexo. Bombelli (1526 – 1572), seu discípulo trabalhava sistematicamente com a quantidade \sqrt{-1} , que hoje chamamos de unidade imaginária e representado por i . Entretanto, apenas no século XIX, quando Gauss divulga a representação geométrica dos números complexos é que essa unidade imaginária começou soar menos desconfortável.
A definição formal de um número complexo
Equações na forma x^2+1=0 são observadas desde os primórdios da matemática e elas deram origem ao que hoje chamado de número complexo e utilizamos na forma geral como $$ z = x + i y; \qquad x,y \in \mathbb{R} \text{ e } \sqrt{-1} = i . $$
Desta forma, fixando um sistema de coordenadas no plano este número complexo z = x+iy pode ser relacionado com o par ordenado P(x,y) , daí, formalmente, temos a seguinte definição de número complexo:
DEFINIÇÃO: Um número complexo z é um par ordenado (x,y) de número reais x e y onde se escreve $$z=(x,y)$$ e denominamos x de parte real e y de parte imaginária de z e escrevemos $$x=Re(z)\;\;\;e\;\;\;y=Im(z).$$
OBSERVAÇÃO: Algumas pontos necessitam de um olhar mais atento.
- Dois números complexos são iguais se, e somente se, suas partes real e imaginária são iguais. Assim, (1,0) = (1,0), mas (1,0) \neq (0,1).
- O ponto (0,1) é denominado unidade imaginária e é denotado por i. Ou seja, $$i=(0,1).$$ Desta forma, (0,y) = y (0,1) = yi. De maneira análoga, podemos encarar (x,0) = x. Assim, $$(x,y) = (x,0)+(0,y) = x(1,0) + y(0,1) = x+iy.$$ Na prática, um número complexo z=(x,y) é representado na forma $$z=x+iy=Re(z)+Im(z) i$$ que é denominada forma cartesiana de z.
- Se Re(z) = 0, então z é chamado de imaginário puro.
O Conjugado de Um Número Complexo
O conjugado de um número complexo z=x+yi é denotado por \overline{z} e é dado por $$\overline{z} = x-yi.$$ É fácil ver que complexos conjugados têm imagens simétricas em realação ao eixo real. Note que o produto $$ z\overline{z} = (x+yi) (x-yi) = x^2 -y^2 i^2 = x^2+y^2 $$ é um número real.
As Propriedades do Conjugado de Um Número Complexo
- Re(z) = \frac{1}{2} (z+\overline{z}) ;
- Im(z) = \frac{1}{2} (z - \overline{z}) ;
- \overline{(z_1 \pm z_2)} = \overline{z_1} \pm \overline{z_2} ;
- \overline{z_1 z_2} = \overline{z_1} \overline{z_2} ;
- \overline{\left( \dfrac{z_1}{z_2} \right)} = \dfrac{\overline{z_1}}{\overline{z_2}} ;
- z\overline{z} = x^2+y^2.
- Se n é um inteiro positivo, \left( \overline{z} \right)^n = \overline{ \left( z \right)^n }.
Operações Envolvendo Números Complexos
Dados dois números complexos z_1 = x_1+y_1 i e z_2 = x_2 + y_2 i definimos a adição e, por consequência, a subtração, z=z_1 \pm z_2, como $$z=z_1 \pm z_2 = (x_1 \pm x_2) + (y_1 \pm y_2)i.$$ Por sua vez, a multiplicação z=z_1 z_2 é dada por $$z= (x_1+y_1 i) (x_2 + y_2 i) = x_1 x_2 +x_1 y_2 i + x_2 y_1 i – y_1 y_2 \\ = (x_1 x_2 – y_1 y_2) + (x_1 y_2 + x_2 y_1) i$$ Desta definição da multiplicação de números complexos, segue que $$i^2 = (0+1.i)^2 = (0.0 – 1.1) + (0.1+ 1.0)i = -1,$$ ou seja, $$\sqrt{-1} = i.$$
A divisão éntre dois números complexos z=\frac{z_1}{z_2}, sendo z_1 e z_2 como definidos anteriormente, se baseia no fato de que z_2 \neq 0 e que exista z=x+yi de modo que z_1=z.z_2. Na prática, a divisão z=\frac{z_1}{z_2} é operada da seguinte forma $$z=\frac{z_1}{z_2} = \frac{z_1}{z_2}.1=\frac{z_1}{z_2}.\frac{\overline{z_2}}{\overline{z_2}}=\frac{(x_1 x_2 -y_1 y_2)}{x_2^2 +y_2^2} + \frac{(x_1 y_2 + y_1 x_2)}{x_2^2 +y_2^2} i$$
EXEMPLO: Considere z_1 = 2+3i e z_2 = 4-i.
1) Os conjugados de z_1 e z_2 são dados por \overline{ z_1 } = 2-3i e \overline{ z_2 }= 4+i.
2) A soma e a subtração entre z_1 e z_2 são dadas por $$ z_1 + z_2 = (2+3i) + (4-i) = (2+4) + (3-1)i = 6 + 2i;$$ $$ z_1 – z_2 = (2+3i) – (4-i) = (2 – 4) + (3+1)i = -2 + 4i. $$
3) O produto z_1 \times z_2 é dado por $$ z_1 \times z_2 = (2+3i) \times (4-i) =8 – 2i+12i-3i^2 = 11 + 10 i.$$
4) Fazendo z_1 = 2+3 i e z_2 = 4 - i , o quociente \dfrac{z_1}{z_2} será dado por $$z=\frac{2+3 i}{4 – i} = \frac{2+3 i}{4 – i}.1=\frac{2+3 i}{4 – i}.\frac{\overline{4 – i}}{\overline{4 – i}}= \frac{8+ 2i +12 i +3 i^2}{16 – i^2} = \frac{5}{17} + \frac{14}{17} i.$$
As Potências da Unidade Imaginária
As potências de i apresentam um comportamento interessante, se repetindo em ciclos quaternários de potência como podemos ver abaixo na tabela:
| i^{0} = 1 | i^{4} = i^{2} \times i^{2} = 1 |
| i^{1} = i | i^{5} = i^{4} \times i = i |
| i^{2} = -1 | i^{6} = i^{4} \times i^{2} = -1 |
| i^{3} = -i | i^{7} = i^{4} \times i^{3} = -i |
Seguindo adiante nesta tabela podemos observar o padrão para as potências da unidade imaginária dado por $$ i^{n+4} = i^{n} \times i^{4} = i^{n} \times 1 = i^{n}.$$ Com isso podemos estabelecer uma regra para o cálculo das potências de i : para calcular i^{n} , divida n por 4 e o resto r desta divisão será a potência equivalente, ou seja, i^n = i^r .
EXEMPLO: Para calcular i^{999\;945\;347}, dividimos 999\;945\;347 por 4 e encontramos resto 3 . Ou seja, $$ i^{999\;945\;347} = i^3 = -i .$$
O Diagrama de de Argand-Gauss
Após um panorama algébrico dos números complexos, vamos passar para um olhar geométrico deste conjunto. A representação geométrica dos números complexos é feita no plano cartesiano, onde o eixo x é denominado eixo real e o eixo y é o eixo imaginário.
Os números representados no eixo dos x são da forma (x,0) = x+0i , ou seja, são os números reais puros, por isto este é chamado de eixo real. Já os complexos representados no eixo dos y , e por isso chamado de eixo imaginário, são da forma 0 + yi = yi. Sendo assim, o número complexo z=x+yi é plotado como o par ordenado (x,y).
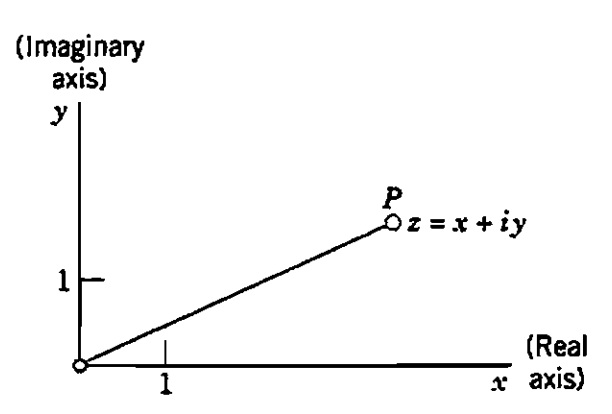 Diagrama de Argand: O Plano Complexo
Diagrama de Argand: O Plano Complexo
O plano xy onde são representados os números complexos é chamado de plano complexo ou diagrama de Argand.
Jean-Robert Argand foi um matemático suíço amador mais conhecido como um dos primeiros a fornecer uma descrição geométrica dos números complexos. Argand publicou em 1806 uma interpretação geométrica dos números complexos, o Diagrama de Argand. Esta descrição geométrica dos números complexos também é associada ao nome de Gauss, embora anteriormente a Gauss, Caspar Wessel também tenha descrito o diagrama.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
A adição e a subtração de dois números complexos, de acordo com a “regra do paralelogramo”, pode ser representado n plano complexo da seguinte forma:
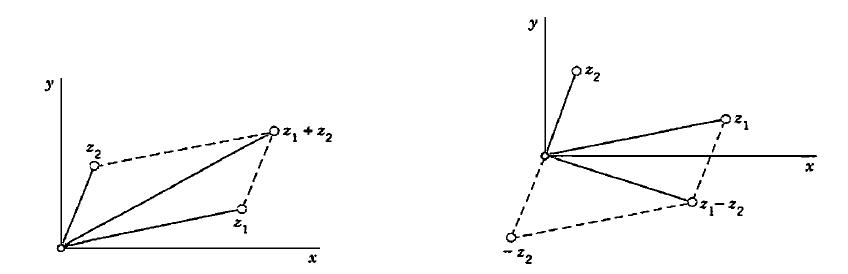 Soma de Números Complexos no Plano de Argand
Soma de Números Complexos no Plano de Argand
O complexo conjugado também pode ser representado no plano complexo. Para exemplificar considere z = 5 + 2i.
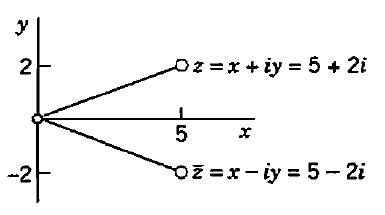 Representação do complexo conjugado no Plano de Argand
Representação do complexo conjugado no Plano de Argand
O Módulo de um Número Complexo
Dado um número z = a +bi , chama-se módulo de z , denotado por | z | , ao número real não negativo $$|z| = \sqrt{a^2 + b^2}.$$ Geometricamente, no plano de Argand, o módulo dá a distância da origem do sistema ao ponto z = (x,y) .
Com esta definição, podemos concluir que $$z\overline{z} = x^2+y^2 = | z |^2, $$ ou seja, o produto de um número complexo com seu conjugado é igual ao quadrado do seu módulo. Além disso, pode-se mostrar que $$ \frac{1}{z} = \frac{\overline{z} }{|z|^2} = \frac{x}{x^2 + y^2} – \frac{y}{x^2 + y^2}i $$ e $$| z_1 \times z_2 | = |z_1| \times |z_2| .$$
Listas de Exercícios Resolvidos:
- A Forma Polar de Um Número Complexo | Lista de Exercícios Resolvidos
- Números Complexos: Módulo e Conjugado | Exercícios Resolvidos
Referências Bibliográficas:
Abaixo seguem os títulos usados como base para este artigo. Para conferir os títulos específicos basta clicar nos links em azul.
- KREYSZIG, E. Advanced Engineering Mathematics, John Wiley & Song, Inc., 8th Edition, 1999.
- ÁVILA, Geraldo S. S. Variáveis Complexas e Aplicações. 3ª Edição. Rio de Janeiro: LTC, 2000.
- ZILL, Dennis G. “Curso Introdutório à Análise Complexa com Aplicações”. 2ª edição, LTC, Rio de Janeiro, 2011
- LIMA, Elon Lages, CARVALHO, Paulo Cezar Pinto, WAGNER, Eduardo e MORGADO, Augusto César. “A Matemática do Ensino Médio, volume 3”.
Leia Mais:
- Números Complexos | A Forma Polar e as Operações Elementares
- Números Complexos | A Exponencial de um Número Complexo
- Funções de Variáveis Complexas | Uma Introdução.
- O que são Conjuntos Numéricos? Dos Naturais aos Complexos.


