O numero π (pi) é a razão entre o comprimento de uma circunferência e seu diâmetro, tendo um valor aproximado de 3,14 ou 3,14159. Embora seja um número irracional, algumas pessoas usam expressões racionais, como 22/7 ou 333/106, para estima-lo.

Introdução
O número π (pi) é uma das constantes matemáticas mais conhecidas e intrigantes da história. Ele aparece em diversas áreas da matemática e da física, sendo utilizado em fórmulas que vão desde o cálculo de áreas de círculos até aplicações mais complexas na engenharia e astronomia.
O π (pi) é um número que relaciona a circunferência de um círculo ao seu diâmetro. Essa relação é explorada em detalhes no artigo “Número pi (π): valor, história, cálculo” do Brasil Escola. Além disso, o π (pi) é um número irracional, o que significa que é um número real que não pode ser expresso por uma fração simples. Isso porque π (pi) é o que os matemáticos chamam de “decimal infinito” – após o ponto decimal, os dígitos continuam para sempre.
\pi ocorre em vários problemas matemáticos envolvendo os comprimentos de arcos ou outras curvas, as áreas de elipses , setores e outras superfícies curvas e os volumes de muitos sólidos. Também é usado em várias fórmulas da física e da engenharia para descrever fenômenos periódicos como o movimento dos pêndulos , a vibração das cordas e as correntes elétricas alternadas.
Qual o Valor de Pi?
- 3,14 (aproximação para cálculos simples);
- 3,14159 (comum em aplicações matemáticas);
- As 100 primeiras casas decimais de pi: 3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679.
 Sugestão de Leitura: “Almanaque das Curiosidades Matemáticas”, de Ian Stewart, com 20% de desconto
Sugestão de Leitura: “Almanaque das Curiosidades Matemáticas”, de Ian Stewart, com 20% de desconto
Quantas Casas Decimais Tem o Número Pi?
A Importância de Pi na Matemática
- Cálculo de áreas e volumes: essencial em círculos, esferas e cilindros;
- Trigonometria: usado em funções trigonométricas como seno e cosseno;
- Análise matemática: aparece em séries infinitas e integrais;
- Ciências aplicadas: em engenharia, astronomia e até na música.
Quais são As 100 primeiras casas decimais do número Pi?
 Aprenda matemática de forma prática e simples com o curso Matemática para ENEM por Vando Mat. Prepare-se para o ENEM e aumente suas chances de sucesso! Saiba mais aqui.
Aprenda matemática de forma prática e simples com o curso Matemática para ENEM por Vando Mat. Prepare-se para o ENEM e aumente suas chances de sucesso! Saiba mais aqui.
A História do Número Pi
Número pi (π): o que é e para que serve
Os Babilônicos descobriram o Número Pi
Pi é conhecido há quase 4.000 anos e foi descoberto pelos antigos babilônios. Um registro em barro datado de algo entre 1900 a.C. e 1680 a.C. descobriu que \pi era já estimado próximo de 3 nesta época. Os babilônios (c. 2000 AC ) usaram 3,125 para aproximar \pi , pois foi um valor que obtiveram calculando o perímetro de um hexágono inscrito em um círculo e supondo que a razão entre o perímetro do hexágono e a circunferência do círculo fosse 24/25.
No antigo Egito estavam fazendo descobertas semelhantes, como evidenciado pelo papiro Rhind de 1650 a.C. Neste documento, os egípcios calcularam a área de um círculo por uma fórmula dando para \pi um valor aproximado de 3,1605. Um dos primeiros cálculos de \pi foi realizado pelo matemático grego Arquimedes de Siracusa (287 a.C. a 212 a.C.).
 Descubra a história fascinante por trás do número π e como o Papiro Rhind, do Egito Antigo, revolucionou os cálculos matemáticos! Compartilhe este artigo com amigos e mergulhe no passado da matemática!
Descubra a história fascinante por trás do número π e como o Papiro Rhind, do Egito Antigo, revolucionou os cálculos matemáticos! Compartilhe este artigo com amigos e mergulhe no passado da matemática!
Arquimédes e o Valor de Pi
Arquimedes usou o teorema de Pitágoras para encontrar as áreas de dois polígonos, aproximou a área de um círculo com base na área de um polígono regular inscrito no círculo e na área de um polígono regular dentro do qual o círculo foi circunscrito. Os polígonos, como Arquimedes os mapeou, deram os limites superior e inferior para a área de um círculo, e ele aproximou pi entre 3 1/7 e 3 10/71, num processo similar ao que mostraremos mais adiante.
Com isso ele deu um grande passo à frente ao conceber um método para obter \pi com qualquer precisão desejada, desde que você tivesse paciência suficiente (um matemático, como veremos à seguir, tentou por 30 anos). Ao inscrever e circunscrever polígonos regulares em torno de um círculo para obter limites superiores e inferiores, ele obteve 223/71 < π < 22/7, ou um valor médio de cerca de 3,1418. Arquimedes também provou que a razão entre a área de um círculo e o quadrado de seu raio é a mesma constante.
Anteriormente, o matemático e astrônomo chinês Zu Chongzhi (429 aC a 501 aC) havia calculado \pi usando um método semelhante, encontrando o valor como 355/113. Infelizmente, o livro de escrita de Zu foi perdido, então pouco se sabe sobre seu trabalho ou métodos.
Origem do Símbolo π
No final do século XVII, no entanto, novos métodos de análise matemática na Europa forneceram maneiras aprimoradas de calcular \pi envolvendo série infinita. Por exemplo, Isaac Newton usou seu teorema binomial para calcular 16 casas decimais rapidamente.
O matemático britânico William Jones foi o primeiro a começar a usar o símbolo \pi para representar esta razão, em 1706. O símbolo π foi adotado por William Jones em 1706, mas só se popularizou com o matemático Leonhard Euler, que o usou amplamente em seus trabalhos. A escolha do símbolo vem da letra grega que representa “perímetro”, indicando a relação entre o perímetro de um círculo e seu diâmetro.
Em 1761 Lambert provou que \pi era irracional, isto é, que não pode ser escrito como uma razão de números inteiros. Em 1882 Lindeman provou que \pi era transcendental, ou seja, que \pi não é a raiz de nenhuma equação algébrica com coeficientes racionais. Essa descoberta provou que não se pode “quadrar um círculo”, o que era um problema que ocupava muitos matemáticos até então.
 Conheça William Jones, o matemático que deu ao número π seu símbolo icônico! Descubra mais sobre sua contribuição no artigo e compartilhe com outros apaixonados por matemática!
Conheça William Jones, o matemático que deu ao número π seu símbolo icônico! Descubra mais sobre sua contribuição no artigo e compartilhe com outros apaixonados por matemática!
Os Computadores deram mais de 1oo casas para o número Pi
No início do século 20, o matemático indiano Srinivasa Ramanujan desenvolveu maneiras excepcionalmente eficientes de calcular \pi que mais tarde foram incorporadas em algoritmos de computador. No início do século 21, os computadores calcularam \pi com 62.831.853.071.796 casas decimais, bem como seu dígito de dois quadrilionésimos quando expresso em binário.
Representação Visual de Pi: O Princípio da Exaustão de Arquimédes.
Como vimos anteriormente, \pi é a razão entre o comprimento de uma circunferência e seu diâmetro, independente de qual seja a circunferência. Sendo C o comprimento da circunferência de raio R , então, por definição: $$ \frac{C}{2R} = \pi .$$ O comprimento da circunferência, é, por definição, o número real cujas aproximações por falta são os perímetros dos polígonos regulares e cujas aproximações por excesso são os perímetros dos polígonos regulares circunscritos.
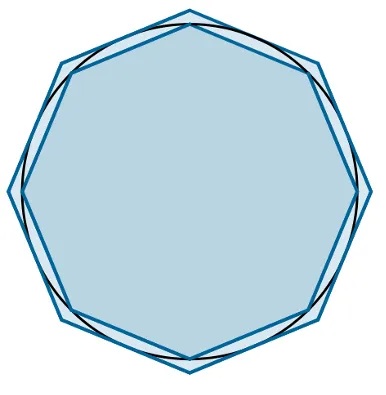 O comprimento da circunferência por definição.
O comprimento da circunferência por definição.
Considere que C é o comprimento da circunferência, p_n o perímetro do polígono inscrito e P_n o perímetro do circunscrito. Desta forma, $$ p_n < C < P_n $$ e quando n cresce, os valores de p_n aumentam e os de P_n diminuem, sendo que ambos se aproximam do valor de C .
Sendo R o raio da circunferência, as razões $$ \frac{p_n}{2R} \qquad e \qquad \frac{P_n}{2R},$$ quando n cresce, vão se aproximando, uma por um lado e outra pelo outro, de $$ \frac{C}{2R},$$ ou seja, de \pi , conforme vemos na tabela abaixo, com polígonos até 384 lados já podemos estimar \pi com as três primeiras casas decimais:

Até por isso, o número \pi é um número irracional, aproximado por 3,1416 . O uso da letra grega \pi para representar a razão entre o comprimento da circunferência e seu diâmetro deve-se a Euler, que a adotou em 1737. Mas esta razão sempre fascinou matemáticos e curiosos de toda a história.
O número \pi ainda aparece na fórmula da área da circunferência, dada por $$ \text{Área da Circunferência } = \pi R^2, $$ que é o número real cujas aproximações por falta são as áreas dos polígonos regulares inscritos, e, consequentemente, na fórmula da áreas de setores circulares, dada por $$ \text{Área do setor circular } = \frac{ \alpha }{360} \pi R^2 $$ sendo \alpha a medida em graus do ângulo central do setor circular.
Lembrando que se L é o comprimento do arco deste mesmo setor circular, podemos garantir que $$ \text{Área do setor circular } = \frac{ \alpha }{360} \pi R^2 = \frac{LR}{2}$$ sendo R o raio da circunferência, uma fórmula bastante interessante, pois dá a ideia de que o setor circular seria um “triângulo” de base de comprimento L e altura R .
Cálculo do Pi Pelo Método dos Polígonos
Na figura abaixo, l_n = AB é o lado do polígono regular de n lados inscrito numa circunferência de raio 1. Se C é o ponto médio do arco AB , então AC = l_{2n} é o lado do polígono regular de 2 n lados inscrito na mesma circunferência .
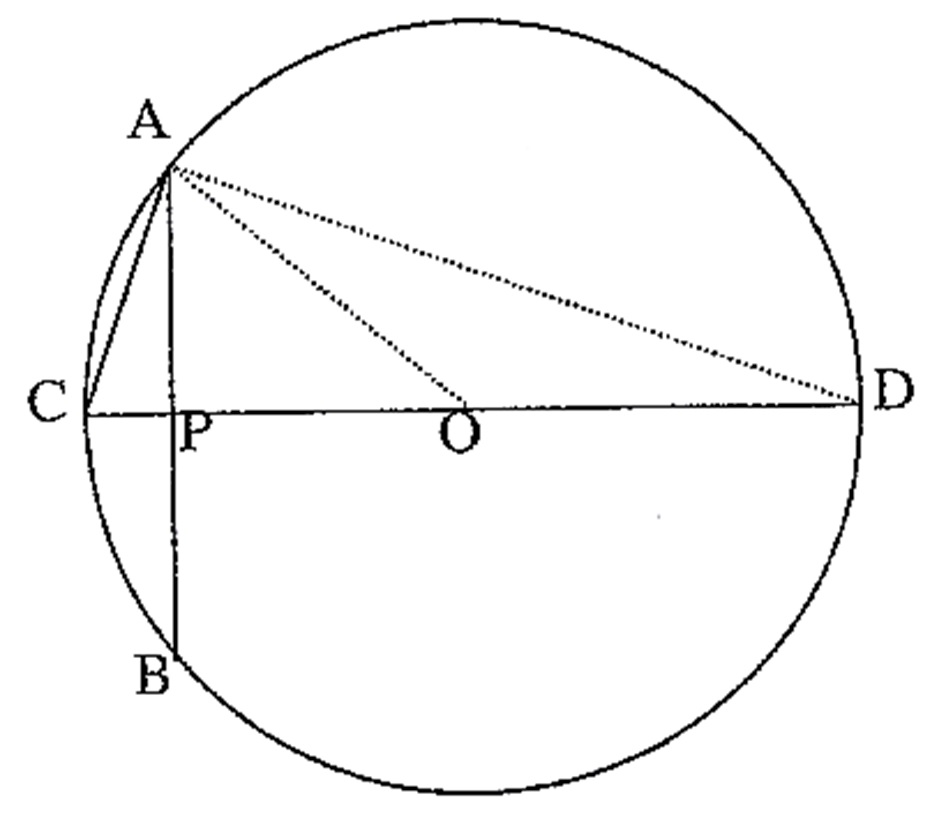
Sendo CD o diâmetro, O o centro da circunferência e P e o ponto de intersecção de AB com CD temos, no triângulo retângulo ACD , a relação $$ AC^2 = CD \cdot CP.$$ Observe que AC = l_{2n} e $$OP = \sqrt{1 – \frac{(l_n)^2}{4} } = \frac{1}{2} \sqrt{4 – (l_n)^2} .$$
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Daí, $$ (l_n)^2 = 2 \left(1 – \frac{1}{2} \sqrt{4 – (l_n)^2} \right) = 2- \sqrt{4 – (l_n)^2} .$$ Assim, $$l_{2n} = \sqrt{2 – \sqrt{4 – (l_n)^2} } .$$ Usando esta fórmula de recorrência podemos inferir que o prímetro do polígono 2^{n+1} lados é igual a 2^{n+1} \cdot l_{2^{n+1}} , que tende a 2 \pi quando n cresce. Assim, aproximações de \pi podem ser obtidas por: $$ \pi \approx 2^{n} \cdot \sqrt{2- \sqrt{2+\sqrt{2 + \sqrt{2 + \sqrt{2+ \sqrt{2+\sqrt{2+\sqrt{…}}}}}}}}$$ onde as reticências representam os n radicais na expressão.
Por mais contraproducente que possa parecer, os matemáticos antigos calculavam essas raízes manualmente, com um número elevado de casas decimais, para conseguirem obter umas poucas casas decimais precisas de \pi . Uma curiosidade interessante é que L.van Ceulen conseguiu 35 casas decimais exatas. Como morreu logo em seguida, a viúva mandou gravar esse valor de \pi em sua lápide: $$3,14159265358979323846264338327950288.$$ Ludolph van Ceulen empreendeu mais de trinta anos da sua vida aperfeiçoando o método de cálculo do número irracional \pi .
A Irracionalidade de Pi que é, também, um número transcendental.
A demonstração de que \pi é um número irracional se mostra muito sofisticada e depende de argumentos que fogem do escopo ilustrativo do nosso artigo. A irracionalidade de \pi foi demonstrada pela primeira vez, no século XVIII, pelo matemático francês Johann Heinrich Lambert. Embora não possamos escrever uma representação numérica exata de \pi , podemos anotar diversas fórmulas que o definem precisamente, e a prova de Lambert utiliza uma destas fórmulas
Mas, intuitivamente, como podemos entender que \pi é irracional? Como pudemos ver pela tabela de razões dos polígonos inscritos e circunscritos na circunferência de raio R , por mais que aperfeiçoemos a aproximação de \pi por uma razão \dfrac{x}{y} usando números cada vez maiores, jamais chegaremos a \pi , pois isso só aconteceria quando o número de lados dos dois polígonos atingisse o infinito. Como isso é impossível, intuitivamente podemos inferir que \pi é irracional.
Mais do que irracional, \pi é um número transcendental, ou seja não satisfaz nenhuma equação algébrica que o relacione aos números racionais. Isso foi provado por Ferdinand Lindemann em 1882, utilizando técnicas de cálculo diferencial e integral, num problema que é equivalente à histórica busca da quadratura do círculo, um problema proposto pelos antigos geômetras gregos consistindo em construir um quadrado com a mesma área de um dado círculo servindo-se somente de uma régua não graduada e um compasso em um número finito de etapas.
Um Estado Norte-Americano Quiz Determinar o valor de Pi por lei
A lei de número 246, aprovada por unanimidade na Assembléia Legislativa de Indiana no ano de 1897, dava poder ao Estado de determinar um valor para \pi . Não se sabe ao certo qual era o valor em questão, pois o documento parece implicar nove valores diferentes, todos eles errados. A proposta foi motivada pelos resultados errados de Edwin J. Goodwin, um médico que estudava matemática e alegava ter trissectado um ângulo, duplicado um cubo e realizado a quadratura do círculo, três problemas demonstrados sem solução.
Em suma, o estado de Indiana estava criando uma nova matemática, onde a quadratura do círculo era possível de ser resolvida, ou seja, esta lei permitia que \pi pudesse ser construído geometricamente. Além disso, seriam possíveis demonstrar sentenças falsas como verdadeiras, por exemplo, que 0 = 1 . Isso abria um precedente intrigante: livraria assassinos da cadeia, que podiam alegar que como 0 = 1 , eles cometeram zero assassinatos. Na verdade, este fato garantiria que poderíamos provar legalmente qualquer afirmação que queríamos. Alem disso, a ciência da computação seria impossível de ser desenvolvida. Mas a lei foi barrada por outro motivo.
Obviamente, esta lei absurda só foi aprovada pois não trazia custo ao Estado, mas os esforços do professor C. A. Waldo, da Academia de Ciências de Indiana, um matemático que visitou a Assembléia quando a lei era discutida, ajudou a clarear os problemas científicos da questão. Porém, os políticos não debateram a validade da matemática em questão apenas decidiram que não se tratava de uma questão sobre a qual poderiam legislar. E adiaram a votação… até hoje!
Conclusão
MATEMÁTICA PARA ENEM Clique aqui e saiba mais
Clique aqui e saiba mais
Bibliografia
- Eduardo Wagner – “Teorema de Pitágoras e Áreas”.
- Michael Spivak – “Calculus”. | Link do Livro
- Ian Stewart – “Almanaque das Curiosidades Matemáticas” | Link do Livro.
- Carl B. Boyer – “História da Matemática” | Link do Livro.


Queria saber o porque o pi foi criado