Multiplicadores de Lagrange – 3ª Lista de Exercícios Resolvidos

Os Multiplicadores de Lagrange se aplicam em muitos casos onde temos o problema de achar os extremos de uma função apresenta-se sujeito a certas condições nas variáveis independentes, que são chamadas de vínculo e o problema correspondente é um problema de extremos condicionados.

Seja f(x,y) diferenciável no aberto A e seja B = \{ (x,y); g(x,y)=0 \}, onde g é diferenciável e possui derivadas parcias contínuas em A e \nabla g(x,y) \neq (0,0), \forall (x,y) \in B. Uma condição necessária para que (x_0,y_0) seja extremante local de f em B é que exista um real \lambda tal que $$\nabla f(x_0, y_0) = \lambda _0 \nabla g(x_0, y_0).$$

Podemos garantir, para uma função f(x,y,z) diferenciável no aberto A \in \mathbb{R} ^3 e para um conjunto B = \{ (x,y,z); g(x,y,z)=0 \}, onde g é diferenciável e possui derivadas parcias contínuas em A e \nabla g(x,y,z) \neq (0,0,0), \forall (x,y,z) \in B, a existencia de um \lambda _0 que satisfaz a relação $$\nabla f(x_0, y_0, z_0) = \lambda _0 \nabla g(x_0, y_0,z_0)$$ para um extremante local (x_0, y_0, z_0) de f.

Multiplicadores de Lagrange – 3ª Lista de Exercícios Resolvidos

1) Calcule a distância da superfície z = x^2 + y^2 +10 ao plano 3x+2y-6z-6=0 . (Lembre-se: a distância entre duas superfícies é menor distância entre dois de seus pontos)

SOLUÇÃO: 

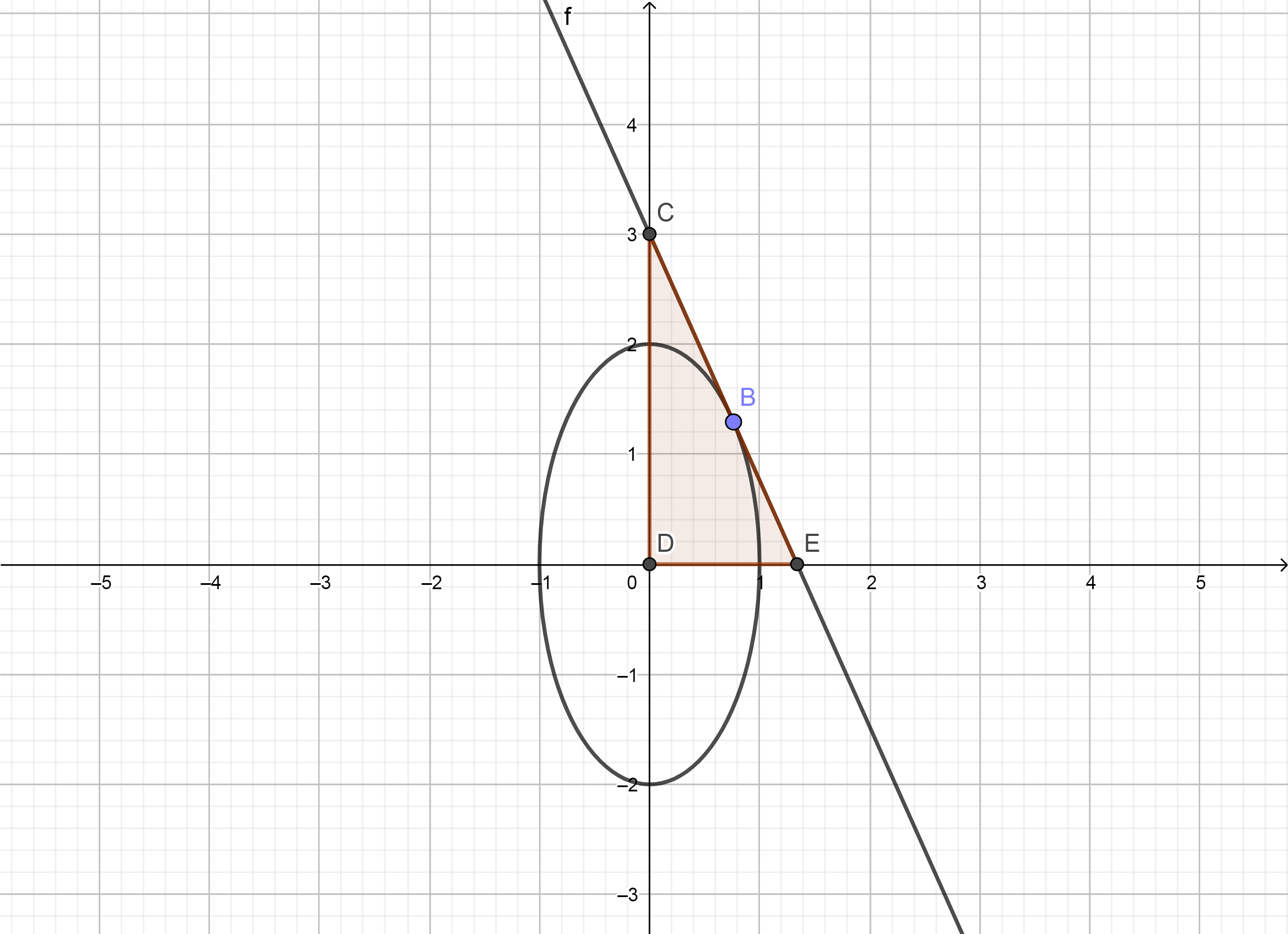
2) Determine a reta tangente à curva x^2 + \dfrac{y^2}{4} = 1, x>0, y>0 que forma com os eixos um triângulo de área mínima.

3) Determinar três números positivos cujo produto seja 100 e cuja soma seja mínima.

Queremos minimizar a função f(x,y,z) = x+y+z sujeita à condição xyz-100 = 0 .

Usando os Multiplicadores de Lagrange, obtemos o sistema $$ \nabla f(x,y,z) = (1,1,1) = \lambda \nabla g(x,y,z) = \lambda (yz, xz, xy) .$$ Desta forma obtemos que $$x=y=z.$$ Assim, substituindo na condição xyz-100 = 0 , obtemos que x=y=z=\sqrt[3]{100} .

4) Encontre e classifique os extremantes de f(x,yz) = xyz, sujeito à condição x^2 + y^2 + z^2 =1 .

SOLUÇÃO: 

Leia Mais:

• Multiplicadores de Lagrange | 1ª Lista de Exercícios Resolvidos
• Máximos e Mínimos de Funções de Várias Variáveis
• Máximos e Mínimos: O Método dos Multiplicadores de Lagrange
• Derivadas Parciais | Funções de Várias Variáveis a Valores Reais
  

Assista Nossa Video Aula: