PRECISANDO DE AJUDA COM SEUS EXERCÍCIOS SOBRE ESTE CONTEÚDO? Entre em contato com a gente via WhatsApp clicando aqui. |
Seja (x_0, y_0) um ponto interior de D_f e suponhamos que \frac{\partial f}{\partial x}(x_0,y_0) e \frac{\partial f}{\partial y}(x_0,y_0) existam. Nestas condições, uma condição necessária para que (x_0, y_0) seja um extremante local de f é que \frac{\partial f}{\partial x}(x_0,y_0) = \frac{\partial f}{\partial y}(x_0,y_0) = 0.
Agora, seja f duas vezes diferenciável e seja (x_0, y_0) um ponto interior do domínio de f. Então:
- Se \frac{\partial^2 f}{\partial x^2} (x_0,y_0) > 0 e H(x_0,y_0) >0, então (x_0,y_0) será um ponto de mínimo local de f
- Se \frac{\partial^2 f}{\partial x^2} (x_0,y_0) < 0 e H(x_0,y_0) >0, então (x_0,y_0) será um ponto de máximo local de f
- Se H(x_0,y_0) < 0, então (x_0,y_0) não será um extremante local, neste caso será um ponto de sela de f.
- Se H(x_0,y_0) = 0 nada podemos afirmar quanto ao ponto (x_0,y_0)
Além disso, se f(x,y) for contínua num conjunto compacto então esta função assumirá um valor de máximo e de mínimo neste conjunto.
Diz-se que (x_0, y_0) é ponto de máximo de uma função f(x,y) se $$f(x,y) \leq f(x_0, y_0)$$ para todo (x,y) \in D_f. Analogamente, (x_0, y_0) é ponto de mínimo de uma função f(x,y) se $$f(x,y) \geq f(x_0, y_0)$$ para todo (x,y) \in D_f.
Vamos analisar e determinar máximos/mínimos de funções de várias variáveis
1) Encontre e classifique os extremantes das funções abaixo:
a) f(x,y) = x^2 + y^2-2x-6y+14
SOLUÇÃO: Os pontos críticos desta função são dados pelas derivadas parciais $$ \frac{\partial f}{\partial x} = 2x – 2 \qquad \frac{\partial f}{\partial y} = 2y – 6 $$ e ambas são iguais a zero simultaneamente no único ponto (1,3) .
Como H(x,y) = 4 e \dfrac{\partial ^2 f}{\partial x^2} = 2 , então qualquer ponto crítico será um ponto de mínimo. Como temos apenas um ponto crítico, ele será um ponto de mínimo global como vemos no gráfico abaixo.
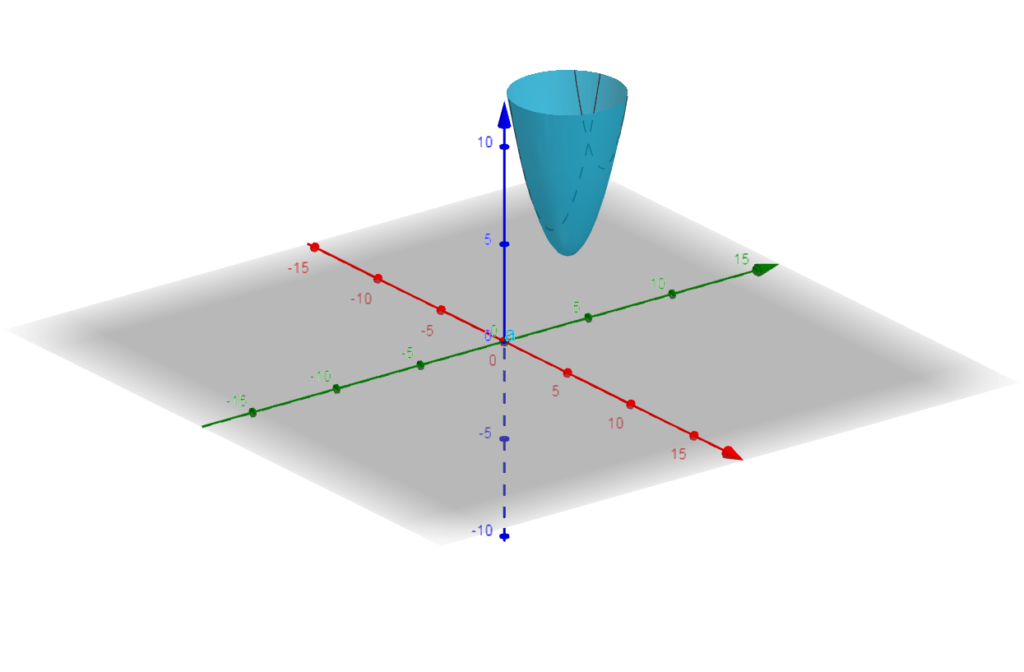
b) f(x,y) = y^2 - x^2 ;
SOLUÇÃO: Os pontos críticos desta função são dados pelas derivadas parciais $$ \frac{\partial f}{\partial x} = – 2x \qquad \frac{\partial f}{\partial y} = 2y $$ e ambas são iguais a zero simultaneamente no único ponto (0,0) . Como H(x,y) = - 4 , então a origem será um ponto de sela como vemos no gráfico abaixo.
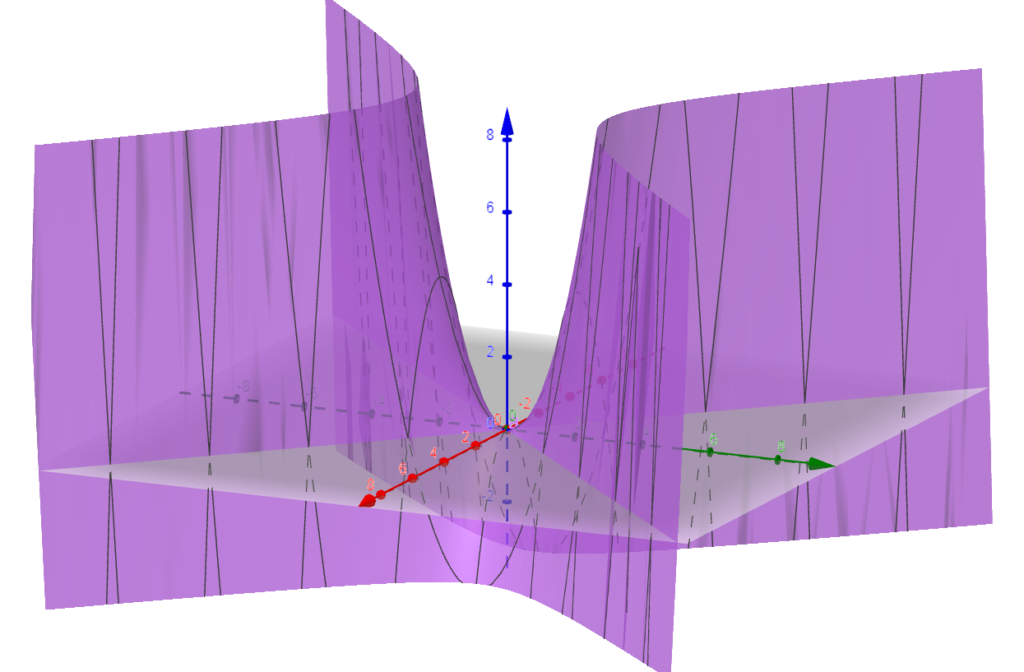
c) f(x,y) = x^4+y^2 - 4xy +1 ;
SOLUÇÃO: Os pontos críticos desta função são dados pelas derivadas parciais $$ \frac{\partial f}{\partial x} = 4x^3 – 4y \qquad \frac{\partial f}{\partial y} = 4 y^3 – 4x $$ que igualadas a zeros geram as equações $$ x^3 – y = 0 \qquad y^3 – x = 0$$ que podem ser resolvidas isolando y = x^3 na primeira equação e substituindo na segundo, nos dando três pontos críticos: $$ P_1(0,0), \qquad P_2(1,1), \qquad P_3(-1, -1) .$$
O determinante hessiano neste caso é dado por $$ H(x,y) = 144 x^2 y^2 – 16$$ e a derivada parcial de segunda ordem com a relação a x é dada por $$ \frac{\partial f}{\partial x} = 12 x^2 $$ que é sempre maior que zero. Desta forma,
- H(0,0) = -16 < 0. Logo, P_1 é um ponto de sela.
- H(1,1) = H(-1,-1) = 128 > 0 . Logo, como \dfrac{\partial f}{\partial x} = 12 x^2 é sempre maior que zero, então P_2 e P_3 são dois pontos de mínimo.
Estes pontos podem ser vistos no gráfico abaixo.
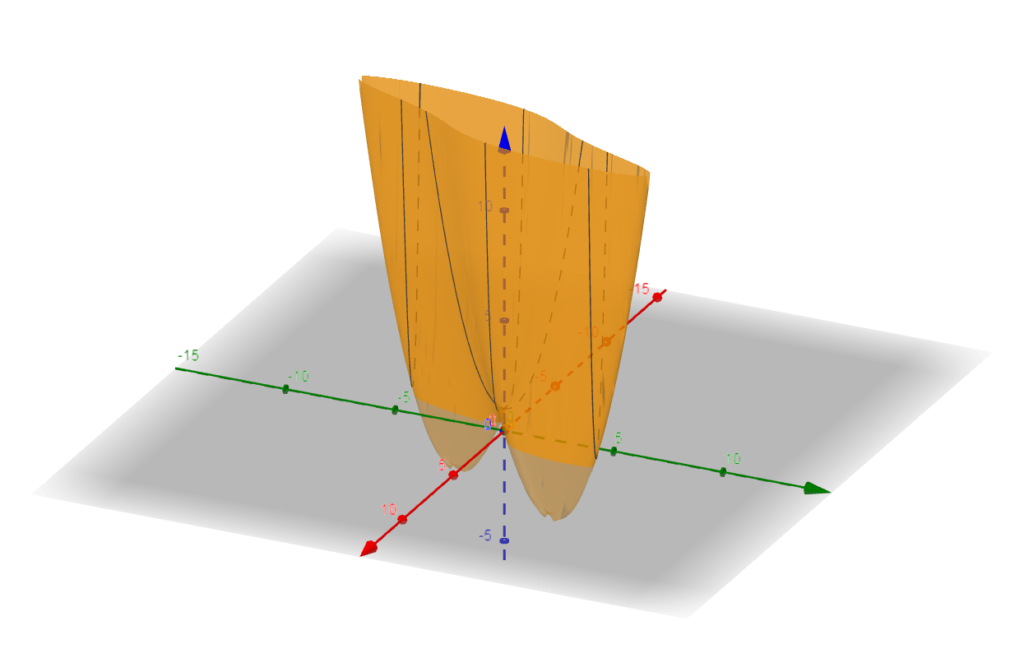
d) f(x,y) = 10 x^2y - 5x^2-4y^2-x^4-2y^4 ;
SOLUÇÃO: Os pontos críticos desta função são dados pelas derivadas parciais $$ \frac{\partial f}{\partial x} = 20 xy – 10 x – 4 x^3 \qquad \frac{\partial f}{\partial y} = 10 x^2 – 8y – 8 y^3 $$ que igualadas a zeros geram as equações $$ 2x (10 y – y – 2x^2) = 0 \;\;\;[1] \qquad e \qquad 5x^2 – 4y -4y^3 = 0 \;\;\;[2] .$$
Da equação [1] teremos $$ x=0 \qquad ou \qquad 10y-5-2x^2 = 0.$$ No primeiro caso, em que x = 0 a equação [2] se torna -4y (1 +y^2) = 0 , cuja solução é dada por y = 0 , logo teremos o ponto crítico (0,0). No segundo caso, em que 10y-5-2x^2 = 0 \Leftrightarrow x^2 = 5y - \dfrac{5}{2} [3] e substituindo na equação [5], obtemos $$25 y – \frac{25}{2} – 4y – 4 y^3 = 0 .$$ Logo, temos que resolver a equação cúbica $$4y^3 – 21 y + \frac{25}{2} = 0 .$$ Por métodos computacionais encontramos como raízes $$ y_1 \approx -2,5452 \qquad y_2 \approx 0,6468 \qquad y_3 \approx 1,8984 .$$ Agora substituindo na equação [3] encontramos os quatro pontos $$ P_{1,2}(\pm 0,8567 ; 0,6468 ) \qquad P_{3,4}( \pm 2,6442 ; 1,8984 )$$ pois para os y_1 \approx -2,5452 não encontramos valores reais para x. Portanto, teremos um total de cinco pontos críticos: $$ P_0 (0,0), \qquad P_{1,2}(\pm 0,8567 ; 0,6468 ) \qquad P_{3,4}( \pm 2,6442 ; 1,8984 ).$$
Agora, observando que $$ \frac{\partial ^2 f}{\partial x^2} =20y-10-12x $$ $$ H(x,y) = -480\,{y}^{2}+288\,x\,y+80\,y+400\,{x}^{2}+96\,x+80 $$ facilmente observamos que os ponto P_0, P_3 e P_4 são pontos de máximo locais e os pontos P_1 e P_2 são pontos de sela, conforme nos mostra a figura abaixo.
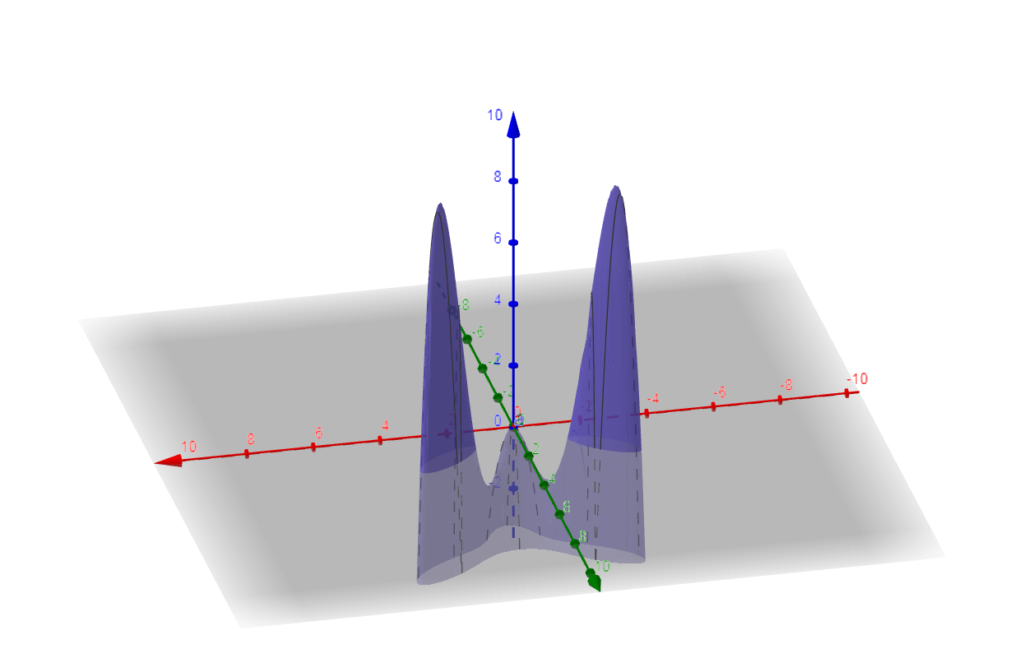
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
2) Encontre e classifique os extremantes de f(x,y) = x^2 +2 y^2 - x restrita ao conjunto x^2 + y^2 \leq 1.
SOLUÇÃO: A figura abaixo ilustra o gráfico da função z=f(x,y) = x^2 +2 y^2 - x e a região x^2 + y^2 \leq 1 sobre o plano xy.
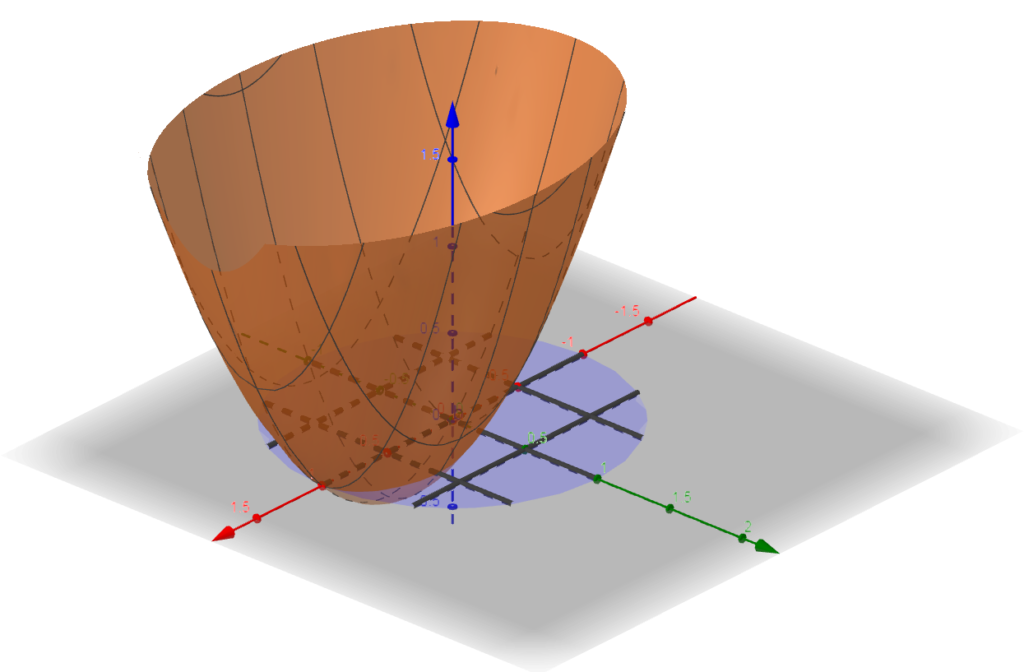
Primeiramente observe que $$ \frac{\partial z}{\partial x} = 2x -1, \qquad \frac{\partial z}{\partial y} = 4y.$$ Desta forma, o ponto crítico da função é dada por \left( \dfrac{1}{2} , 0 \right) , para o qual f\left( \dfrac{1}{2} , 0 \right) = - \frac{1}{4}.
Considere agora o conjunto $$E = \left\{ (x,y) \in \mathbb{R} ^2 | x^2 + y^2 \leq 1 \right\}.$$ Observe que \left( \dfrac{1}{2} , 0 \right) é um ponto interno deste conjunto, logo, este é um extremante da função neste conjunto.
Precisamos agora verificar os pontos da fronteira de E . A fronteira de E é dada pelos pontos do plano tais que x^2 + y^2 = 1 . Logo $$ z = 2 – x-x^2, \qquad com\;\;\; -1 \leq x \leq 1,$$ que é uma função de uma variável restrita ao intervalo [-1,1]. Usando técnicas de cálculo para máximos e mínimos de funções de uma varável, encontramos um ponto de máximo absoluto sobre a fronteira de E em x = - 1/2 (com imagem dada por 9/4 ) e um mínimo absoluto sobre a fronteira de E em x = 1 (com imagem dada por 0 ).
Portanto, o máximo absoluto acontece em \left( - \frac{1}{2} , \pm \frac{\sqrt{3}}{2} \right) e o mínimo absoluto ocorre em \left( \dfrac{1}{2} , 0 \right) .
Leia Mais:
- Máximos e Mínimos de Funções de Várias Variáveis
- Máximos e Mínimos de Campos Escalares | 2ª Lista de Exercícios Resolvidos
- Máximos e Mínimos de Campos Escalares | 1ª Lista de Exercícios Resolvidos
- Maximos e Mínimos: O Método dos Multiplicadores de Lagrange
