Máximos e Mínimos de Campos Escalares | 1ª Lista de Exercícios Resolvidos

Diz-se que (x_0, y_0) é ponto de máximo de uma função f(x,y) se $$f(x,y) \leq f(x_0, y_0)$$ para todo (x,y) \in D_f. Analogamente, (x_0, y_0) é ponto de mínimo de uma função f(x,y) se $$f(x,y) \geq f(x_0, y_0)$$ para todo (x,y) \in D_f.

Seja (x_0, y_0) um ponto interior de D_f e suponhamos que \frac{\partial f}{\partial x}(x_0,y_0) e \frac{\partial f}{\partial y}(x_0,y_0) existam. Nestas condições, uma condiçao necessária para que (x_0, y_0) seja um extremante local de f é que \frac{\partial f}{\partial x}(x_0,y_0) = \frac{\partial f}{\partial y}(x_0,y_0) = 0.

Agora, seja f duas vezes diferenciável e seja (x_0, y_0) um ponto interior do domínio de f. Então:

1. Se \frac{\partial^2 f}{\partial x^2} (x_0,y_0) > 0 e H(x_0,y_0) >0, então (x_0,y_0) será um ponto de mínimo local de f
2. Se \frac{\partial^2 f}{\partial x^2} (x_0,y_0) < 0 e H(x_0,y_0) >0, então (x_0,y_0) será um ponto de máximo local de f
3. Se H(x_0,y_0) < 0, então (x_0,y_0) não será um extremante local, neste caso será um ponto de sela de f.
4. Se H(x_0,y_0) = 0 nada podemos afirmar quanto ao ponto (x_0,y_0)

1ª Lista de Exercícios Resolvidos sobre Máximos e Mínimos

1. Encontre e classifique, se possível, os extremantes de f(x,y) = x^3-3x^2y+27y.

Nesse caso

$$\frac{\partial f}{ \partial x} (x,y) = 3x^2 – 6xy$$

$$\frac{\partial f}{ \partial y} (x,y) = -3x^2 + 27$$ e os únicos pontos que zeram as duas derivadas parciais simultaneamente são (-3,-3/2) e (3,3/2).

Como H(x,y) = -36 x^2, que é sempre um número real menor que zero, então ambos são pontos de sela.

2. Determine, se existirem, os extremantes das funções abaixo, e classifique-os.

a. f(x,y) = 5x^4y^2+xy^3 +4

Primeiramente vamos investigar a existência de pontos críticos, os candidatos a extremantes locais dessa função:

$$ \frac{\partial f}{\partial x} = 20 x^3 y^2 + y^3 = 0$$

$$ \frac{\partial f}{\partial x} = 10x^4 y + 3xy^2 = 0 $$

Da primeira linha encontramos $$ y^2 (20x^3 +y) = 0 \Rightarrow y=0\;\;\; ou \;\;\; y = -20 x^3.$$ Se y = -20 x^3 então encontramos $$x^4 (-200 x^3 -60) = 0 \Rightarrow x= 0 \;\;\; ou \;\;\; x=-\sqrt[3]{\frac{3}{10}}$$

Oque nos dá dois pontos candidatos a extremantes: $$ (0,0) \;\;\;e\;\;\; \left( -\sqrt[3]{\frac{3}{10}}, 6 \right).$$

Como H(x,y) = (60x^2 y^2)(10x^4 +6xy) - (40x^3y+3y^2) = -9y^4 + 120x^3y^3 - 1000x^6y^2, então, encontramos

1. H(0,0) = 0 , ou seja, nada podemos concluir.
2. H \left( -\sqrt[3]{\frac{3}{10}}, 6 \right) = - 22680 , ou seja, \left( -\sqrt[3]{\frac{3}{10}}, 6 \right) é ponto de sela.

O gráfico dessa função pode ser visto abaixo, onde essas conclusões podem ser observadas:

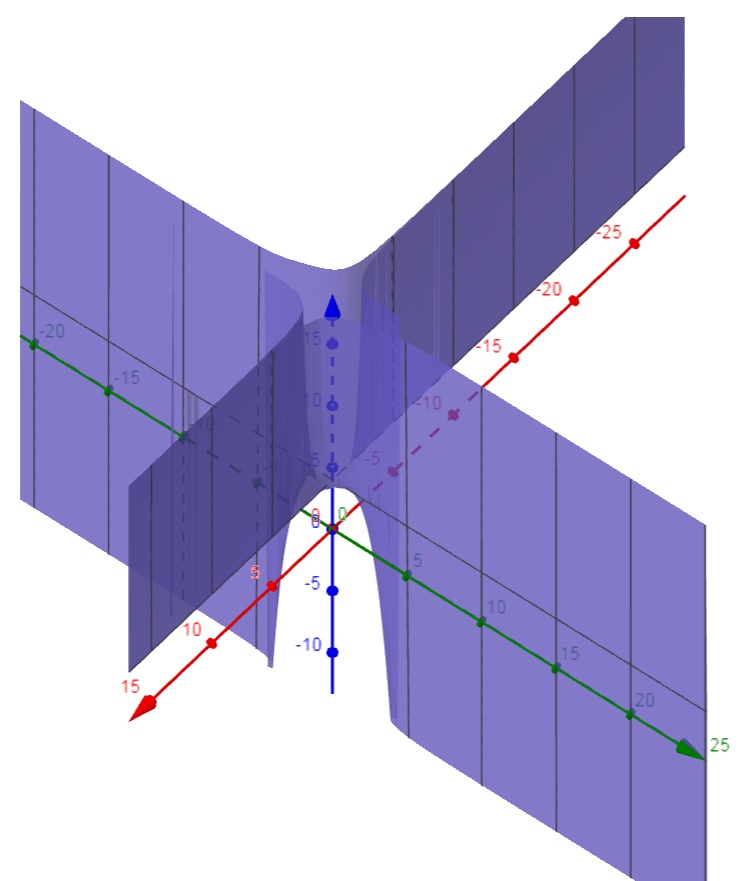
b. z = x^2 + 3 y^2

Nesse caso, apenas o ponto (0,0) satisfaz as equações

$$ \frac{\partial f}{\partial x} = 2x = 0$$

$$ \frac{\partial f}{\partial x} = 6y = 0 .$$

Desta forma, o único candidato a extremante de f(x,y) é  (x,y) = (0,0) .

Como H(x,y) = 12 >0 e como $$ \frac{\partial ^2 f}{\partial x^2} (x,y) = 2 >0, \;\;\; \forall (x,y) \in \mathbb{R}$$ então  (0,0) é ponto de mínimo de f(x,y) = x^2 + 3 y^2 .

Isso está bem ilustrado no gráfico abaixo:

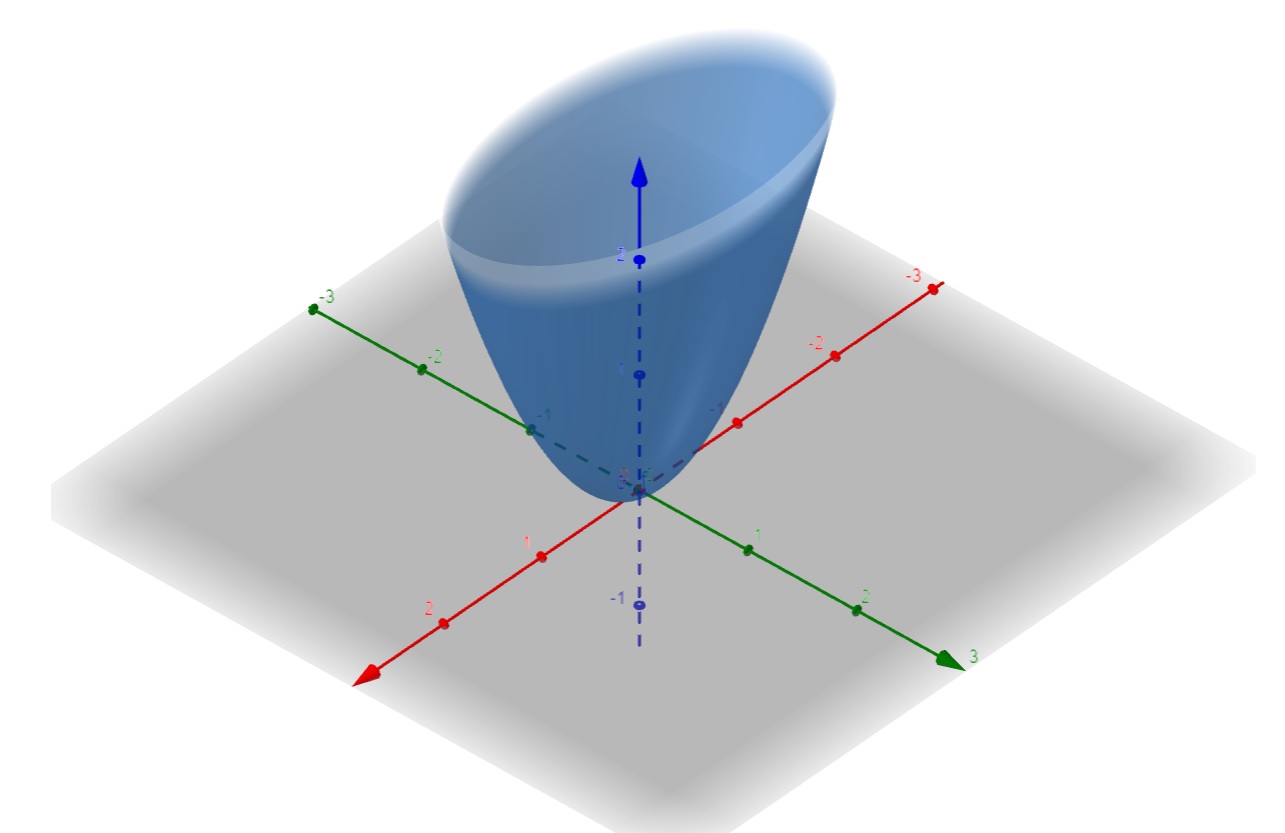
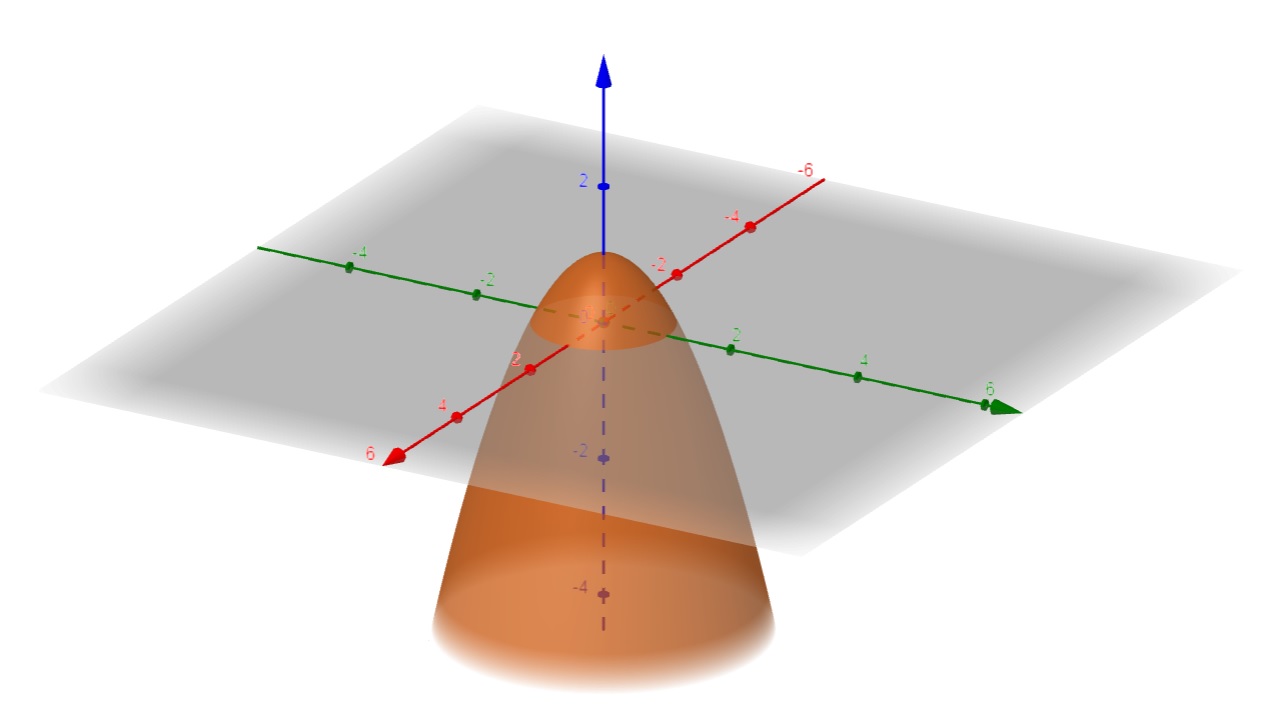
c. f(x,y) = 1 - x^2 - y^2

Nesse caso, também, apenas o ponto (0,0) satisfaz as equações

$$ \frac{\partial f}{\partial x} = -2x = 0$$

$$ \frac{\partial f}{\partial x} = -2y = 0 .$$

Como H(x,y) = 4 >0 e como $$ \frac{\partial ^2 f}{\partial x^2} (x,y) = -2 <0, \;\;\; \forall (x,y) \in \mathbb{R}$$ então  (0,0) é ponto de máximo de f(x,y) = 1 - x^2 - y^2 , como podemos ver no gráfico abaixo:

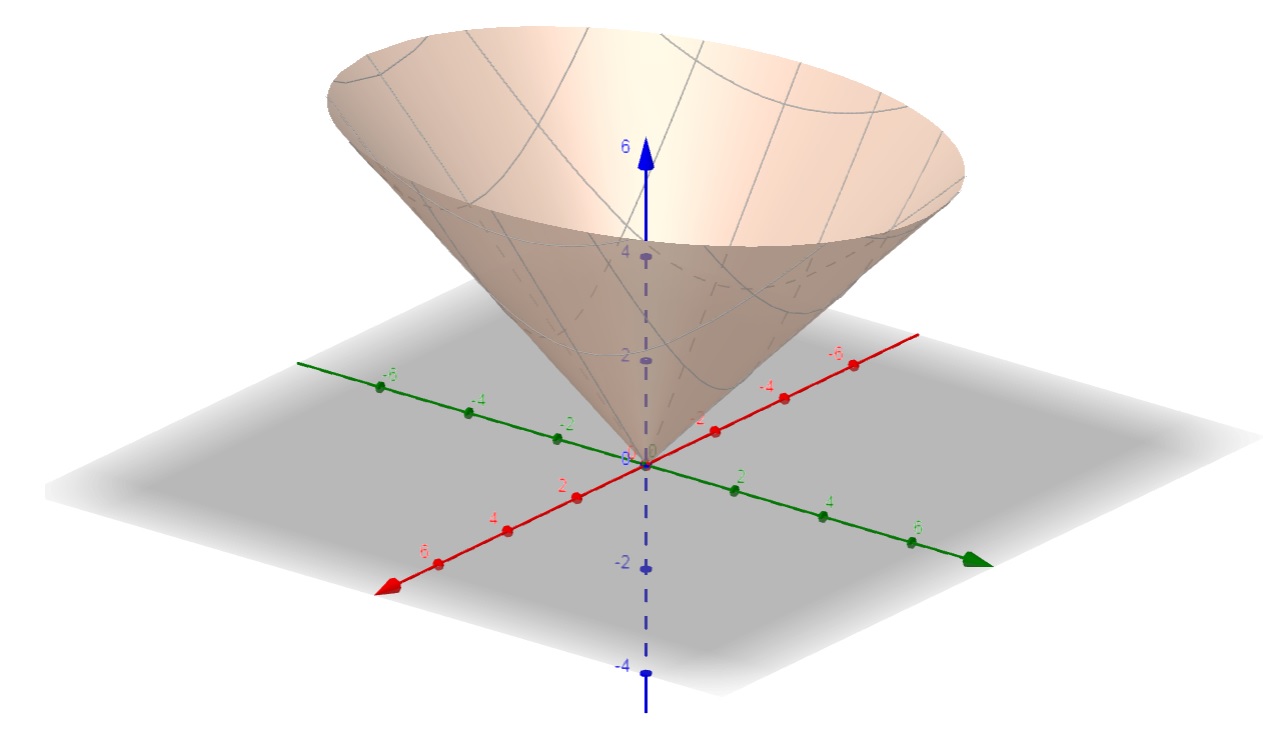
d. f(x,y) = \sqrt{2x^2+y^2}

Nesse caso, também, apenas o ponto (0,0) satisfaz as equações, afinal

$$ \frac{\partial f}{\partial x} = \frac{2x}{\sqrt{2x^2 + y^2}} = 0 \Leftrightarrow 2x=0$$

$$ \frac{\partial f}{\partial x} = -\frac{y}{\sqrt{2x^2 + y^2}} = 0 \Leftrightarrow y=0$$

Porém, como $$\frac{\partial f}{\partial x} (0,0) = \lim_{h \rightarrow 0}{\frac{\sqrt{2h^2}-0}{h}},$$ e esse limite não existe, a função não pode ser diferenciável no ponto (0,0). Desta forma, esse ponto não pode ser um extremante de f(x,y).

Isso fica claro no gráfico abaixo da função, onde percebemos, de fato, não admitir plano tangente no ponto (0,0,0) pela característica da superfície nesse ponto.

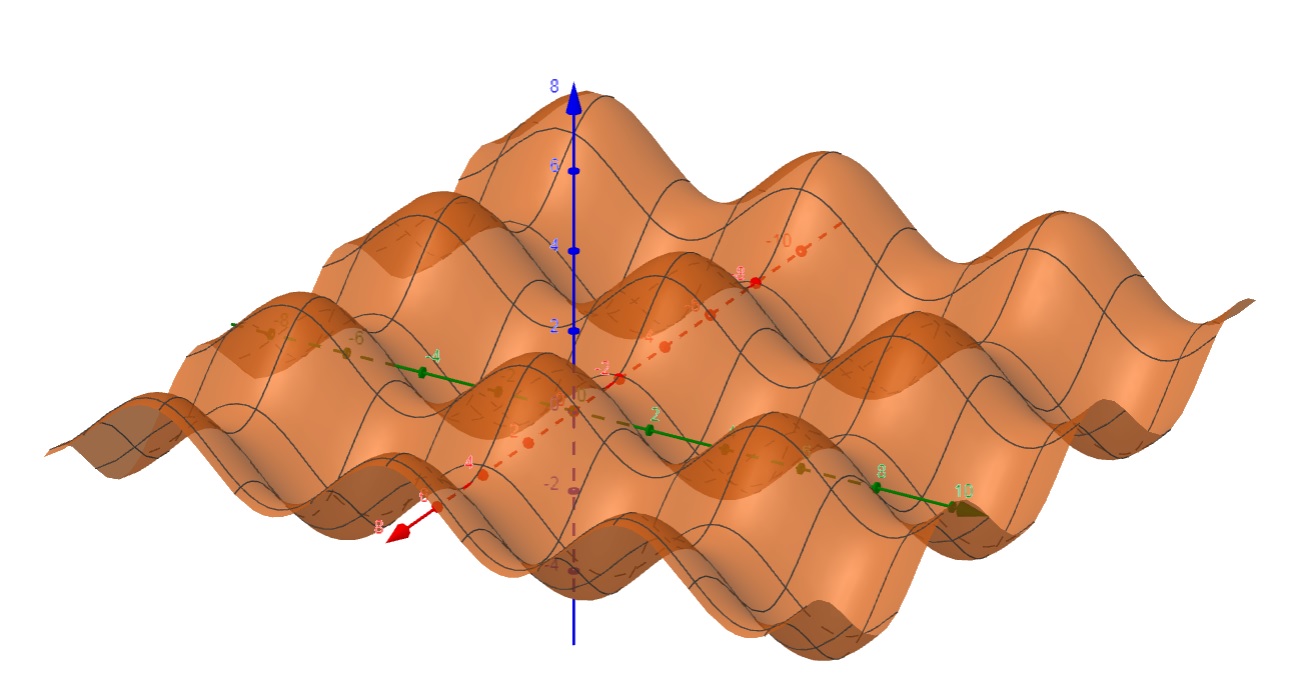
e. f(x,y) = sen(x) + cos (y)

Observe que nesse caso teremos infinitos pontos candidatos a extremantes:

$$ \frac{\partial f}{\partial x} = cos(x) = 0 \Leftrightarrow x = \frac{\pi}{2} + k \pi;\;\;\;k \in \mathbb{Z}$$

$$ \frac{\partial f}{\partial x} = -sen(y) = 0 \Leftrightarrow y = k \pi;\;\;\;k \in \mathbb{Z}$$

Portanto, todos os extremantes são da forma $$(x,y) = \left( \frac{\pi}{2} + k \pi ,  k \pi \right);\;\;\;k \in \mathbb{Z}.$$

Como H(x,y) = sen(x) cos (y) então $$H\left( \frac{\pi}{2} + k \pi ,  k \pi \right) = sen\left( \frac{\pi}{2} + k \pi \right)cos \left( k \pi \right) = 1,$$ pois, \left( \frac{\pi}{2} + k \pi \right)cos \left( k \pi \right) = (-1)\times (-1) se k é ímpar, ou \left( \frac{\pi}{2} + k \pi \right)cos \left( k \pi \right) = (1)\times (1) se k é par.

Logo, cada um desses pontos pode ser um ponto máximo ou ponto de mínimo. Para isso olhamos para a segunda derivada parcial de f com relação a x. Como \dfrac{\partial ^2 f}{\partial x^2} (x,y) = -sen(x) , então:

$$\frac{\partial ^2 f}{\partial x^2} \left( \frac{\pi}{2} + k \pi ,  k \pi \right) = -sen\left( \frac{\pi}{2} + k \pi\right) = \left\{ \begin{array}{lll}
1 & ; & k\;\;\;é\;\;\;ímpar\\
-1& ; & k\;\;\;é\;\;\;par\\
\end{array} \right. $$

Desta forma, \left(\dfrac{\pi}{2} +(2k+1) \pi, (2k+1) \pi \right) é ponto de mínimo e \left(\dfrac{\pi}{2} +2k \pi, 2k \pi \right) é ponto de máximo, para cada número inteiro k. 

Isso pode ser visto no gráfico da função abaixo, que se assemelha a uma “cartela de ovo”:

Leia Mais:

• Máximos e Mínimos de Funções de Várias Variáveis
• Máximos e Mínimos de Campos Escalares | 2ª Lista de Exercícios Resolvidos
• Máximos e Mínimos de Campos Escalares | 3ª Lista de Exercícios Resolvidos
• Maximos e Mínimos: O Método dos Multiplicadores de Lagrange

Assista Nossa Vídeo-Aula Sobre Máximos e Mínimos: