As integrais triplas podem ser calculadas de maneira análoga às integrais duplas, estendendo os conceitos de integrações sucessivas e de mudança de variáveis. De forma análoga à realizada para as integrais duplas podemos definir novas variáveis de integração em uma integral tripla $$I = \int \int_{T} \int{f(x,y,z)dxdydz}.$$
Introduzindo novas variáveis de integração u,v,w por meio de equações x=x(u,v,w), y=y(u,v,w) e z=z(u,v,w), a integral original pode ser expressa como
$$I = \int \int_{T} \int{f(x,y,z)dxdydz} = \int \int_{T} \int{f(x(u,v,w), y(u,v,w), z(u,v,w))\left| \frac{\partial (x,y,z)}{\partial (u,v,w)} \right| dudvdw}$$ onde o determinante jacobiano de x,y e z em relação a u, v e w dado por $$\left| \frac{\partial (x,y,z)}{\partial (u,v,w)} \right| = \left| \begin{array}{ccc}
\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w}\\
\\
\frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w}\\
\\
\frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w}\\\end{array}
\right|$$
| Mais abaixo, neste artigo, temos uma lista com vários exercícios resolvidos sobre a mudança de variável para Integrais Triplas. |
Coordenadas Cilíndricas
As coordenadas cilíndricas de um ponto P, cujas coordenadas cartesianas são (x,y,z), no espaço são dadas por $$r, \theta, z$$ onde r e \theta são as coordenadas polares da projeção de P sobre o plano xy .
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
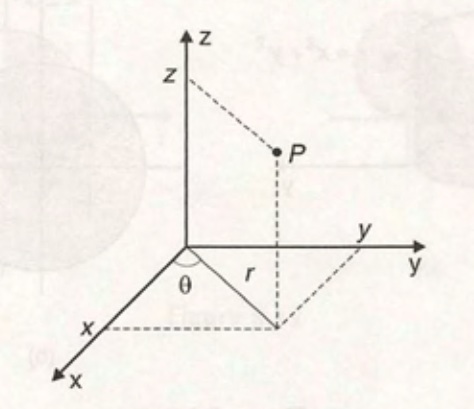 Coordenadas Cilíndricas
Coordenadas Cilíndricas
Desta forma, $$x(r, \theta, z) = r \cos{\theta},$$ $$y(r, \theta, z) = r \sin{\theta}$$ e z(r, \theta, z)=z e o determinate jacobiano é dado por $$\left| \frac{\partial (x,y,z)}{\partial (u,v,w)} \right| = \left| \begin{array}{ccc}
\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial z}\\
\\
\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial z}\\
\\
\frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial z}\\\end{array}
\right| = \left| \begin{array}{ccc}
\cos{\theta} & – r \sin{\theta} & 0\\
\\
\sin{\theta} & r \cos{\theta} & 0\\
\\
0 & \frac{\partial z}{\partial v} & 1\\\end{array}
\right| = r.$$
Portanto, a integração tripla em coordenadas cilindricas é dada por $$I = \int \int_{T} \int{f(x,y,z)dxdydz} = \int \int_{T’} \int{f(r \cos{\theta}, r \sin{\theta}, z)r drd\theta dz}$$ onde T' é a região T descrita em coordenadas cilíndricas.
EXEMPLO
Calcule $$I = \int \int_{T} \int{\sqrt{x^2+y^2+z^2}dxdydz},$$ onde T é o cilindro x^2+y^2 \leq 1, 0\leq z\leq 1.
Em coordenads cilindricas, $$x=r \cos{\theta}, y=r\sin{\theta}, z=z$$
\begin{eqnarray*}
\int \int_{T} \int{\sqrt{x^2+y^2+z^2}dxdydz} & = & \int\limits_{0}^{1} \int\limits_{0}^{ 2\pi} \int\limits_{0}^{ 1}{\sqrt{r^2+ z^2}rdrd\theta dz}\\
& = & \int\limits_{0}^{1} \int\limits_{0}^{ 2\pi}\left[ \frac{1}{3}(z^2+1)^{\frac{3}{2}}- \frac{1}{3}z^3\right]d\theta dz\\
& = & \int\limits_{0}^{1} 2\pi \left[ \frac{1}{3}(z^2+1)^{\frac{3}{2}}- \frac{1}{3}z^3\right]d\theta dz\\
& = & \frac{2}{3}\pi \left[ \overbrace{\int\limits_{0}^{1} (z^2+1)^{\frac{3}{2}}dz}^{(*)} – \int\limits_{0}^{1} z^3dz\right]\\
& = & \frac{2}{3}\pi \left[ \frac{\sqrt{2}}{2}+\frac{3\sqrt{2}}{8} + \frac{3}{8}\ln{(\sqrt{2}+1)} – \frac{1}{4} \right]\\
\end{eqnarray*}
Para solucionar a integral dada em (*) basta fazer a substituição z=\tan{\theta} e lembrar que dz=\sec^2{\theta}d\theta. Após a substituição, utilize a fórmula de recorrencia $$\int{\sec^{n}{\theta}d{\theta}} = \frac{1}{n-1}\sec^{n-2}{\theta}\tan{\theta}+\frac{n-2}{n-1}\int{\sec^{n-2}{\theta}d{\theta}}.$$
Coordenadas Esféricas
As coordenadas esféricas de um ponto P, cujas coordenadas cartesianas são (x,y,z), no espaço são dadas por $$r, \theta, \phi$$ onde r é a distância de P até a origem, \theta é mesma das coordenas cilindricas e \phi é o ângulo formado pelo eixo positivo dos z e o segmento que une o ponto P à origem.
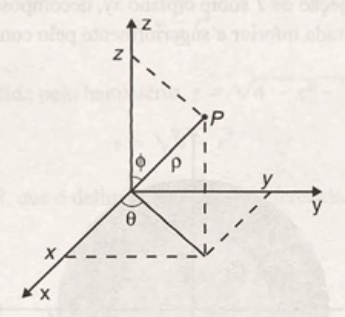 Coordenadas Esféricas
Coordenadas Esféricas
Desta forma, $$x(r, \theta, \phi) = r \cos{\theta}\sin{\phi},$$ $$y(r, \theta, \phi) = r \sin{\theta}\sin{\phi}$$ e z(r, \theta, \phi)=r \cos{\phi} e o determinate jacobiano é dado por $$\left| \frac{\partial (x,y,z)}{\partial (r, \theta , \phi)} \right| = \left| \begin{array}{ccc}
\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial \phi}\\
\\
\frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial \phi}\\
\\
\frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial \phi}\\\end{array}
\right| = \left| \begin{array}{ccc}
\cos{\theta}\sin{\phi} & -r \sin{\theta} \sin{\phi} & r \cos{\theta} \cos{\phi}\\
\\
\sin{\theta}\sin{\phi} & r \cos{\theta} \sin{\phi} & r \cos{\theta} \sin{\phi}\\
\\
\cos{\phi} & 0 & -r\sin{\phi}\\\end{array}
\right| = r^2\sin{\phi}.$$
Portanto, a integração tripla em coordenadas esféricas é dada por $$I = \int \int_{T} \int{f(x,y,z)dxdydz} = \int \int_{T’} \int{f(r \cos{\theta}\sin{\phi}, r \sin{\theta}\sin{\phi}, r\cos{\phi})r^2\sin{\phi} drd\theta d\phi }$$ onde T' é a região T descrita em coordenadas esféricas.
EXEMPLO
Calcule a massa da esfera x^2 + y^2 + z^2 \leq 1, supondo que a densidade no ponto (x,y,z) é igual a distância deste ponto à origem e que o cálculo da massa é dado por $$\int \int_{T} \int{\delta(x,y,z)dxdydz}$$ sendo \delta(x,y,z) a função densidade volumétrica de massa associada a T.
Utilizando-se de coordenadas esféricas obtemos $$x(r, \theta, \rho) = r \cos{\theta}\sin{\phi},$$ $$y(r, \theta, \rho) = r \sin{\theta}\sin{\phi},$$
$$ \int \int_{T} \int{\sqrt{x^2+y^2+z^2}dxdydz} = $$
$$= \int\limits_{0}^{1} \int\limits_{0}^{ 2\pi} \int\limits_{0}^{\pi}{\sqrt{(r \cos{\theta}\sin{\phi})^2+ (r \sin{\theta}\sin{\phi})^2 + (r \cos{\phi})^2}r^2\sin{\phi}drd\theta d\phi} = $$
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
$$ = \int\limits_{0}^{1} \int\limits_{0}^{ 2\pi} \int\limits_{0}^{\pi}{r^3\sin{\phi}}drd\theta d\phi = $$
$$ = \int\limits_{0}^{1} \int\limits_{0}^{ 2\pi}\left[- r^3 \cos{\phi}\right]^{\pi}_{0} drd\theta= $$
$$ = \int\limits_{0}^{1} \int\limits_{0}^{ 2\pi}2 r^3drd\theta= $$
$$ = \int\limits_{0}^{1} 4\pi r^3 dr= $$ $$ = \pi $$
Exercícios Resolvidos sobre Integrais Triplas
- Integrais Triplas | 1ª Lista de Exercícios Resolvidos
- Mudança de Variável em Integrais Triplas | 1ª Lista de Exercícios Resolvidos
- Volume com Integrais Triplas | 1ª Lista de Exercícios Resolvidos
Leia Mais:
- Calculando Volume com Integrais Triplas
- As Integrais Triplas | Funções da Várias Variáveis
- Calculando Volume e Área de Superfície com Integrais Duplas
- Mudança de Variável em Integrais Triplas | 1ª Lista de Exercícios Resolvidos


