Integrais Duplas | 2ª Lista de Exercícios Resolvidos

As integrais duplas são calculadas usando o Teorema de Fubini: Seja f(x,y) integrável no retângulo R=\{ (x,y)\in \mathbb{R}^2 ; a \leq x \leq b, c\leq y \leq d \}. Suponhamos que as integrais $$\int_{a}^{b}{f(x,y)dx}, \forall y\in[c,d]$$ e $$\int_{c}^{d}{f(x,y)dy}, \forall x \in[a,b].$$ Então, $$\int_{c}^{d} \int_{a}^{b}{f(x,y)dx} dy = \int_{c}^{d}\left( \int_{a}^{b}{f(x,y)dx} \right) dy = \int_{a}^{b}\left( \int_{c}^{d}{f(x,y)dy} \right) dx.$$

As integrais duplas possuem propriedades comuns às integrais simples. A linearidade da integral dupla se expressa através das equações: $$\int \int_{R}{c f(x,y)}dxdy = c \int \int_{R}{f(x,y)}dxdy$$ $$\int \int_{R}{f(x,y)+g(x,y)}dxdy. = \int \int_{R}{f(x,y)}dxdy + \int \int_{R}{g(x,y)}dxdy,$$ onde c é uma constante e f e g são contínuas no dóminio fechado e limitado R.

Além disso, se R = R_1 \cup R_2, então $$\int \int_{R}{f(x,y)}dxdy. = \int \int_{R}{f(x,y)}dxdy + \int \int_{R_2}{f(x,y)}dxdy.$$ Se f(x,y) \geq g(x,y), \forall (x,y) \in R, então $$\int \int_{R}{f(x,y)}dxdy \geq \int \int_{R}{g(x,y)}dxdy,$$ por consequência, se f(x,y) \geq 0 teremos $$\int \int_{R}{f(x,y)}dxdy \geq 0.$$

2ª Lista de Exercícios Resolvidos Sobre Integrais Duplas

1) Calcule \int\limits_{R} \int{f(x,y)dxdy} onde:

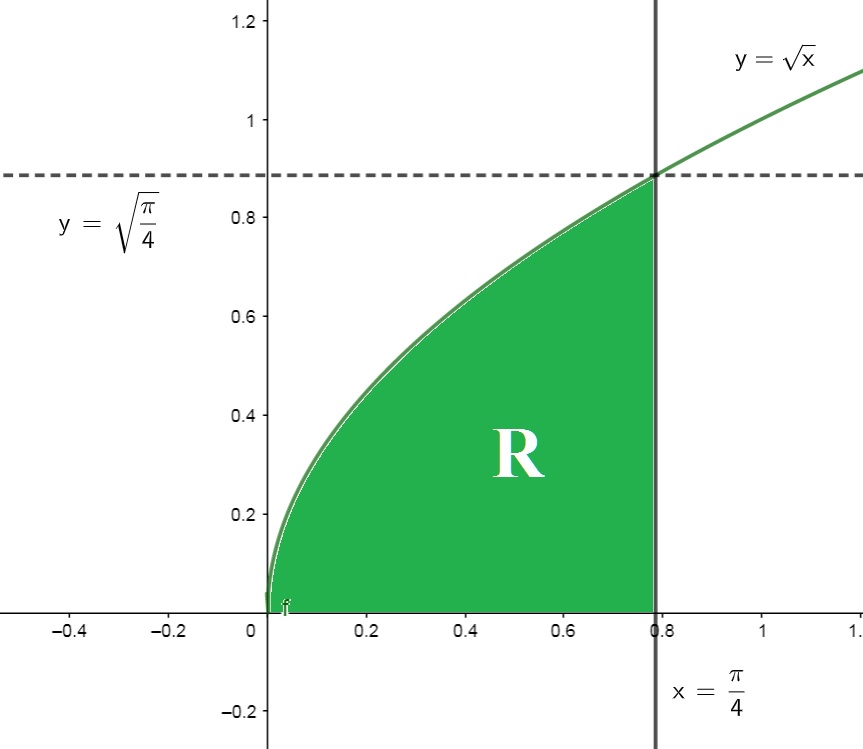
(a) f(x,y) = \sqrt{x}cos(y \sqrt{x}) e R é o domínio delimitado por y = \sqrt{x}, x = \dfrac{\pi}{4} e y = 0 .

SOLUÇÃO: Observe que pela representação gráfica da região R dada abaixo, podemos escrevê-la como $$R: \left\{ \begin{array}{l}
0 \leq y \leq \sqrt{x}\\
0 \leq x \leq \frac{\pi}{4}
\end{array} \right. \;\;\;\;ou\;\;\;\;R: \left\{ \begin{array}{l}
y^2 \leq x \leq \frac{\pi}{4}\\
0 \leq y \leq \sqrt{\frac{\pi}{4}}
\end{array} \right. $$

A função de integração pede (por uma questão de simplicidade) que integremos primeiro para a variável y, logo $$ \int\limits_{R} \int{\sqrt{x}cos(y \sqrt{x})dxdy} = \int\limits_{0}^{\pi/4} \int\limits_{0}^{\sqrt{x}}{\sqrt{x}cos(y \sqrt{x})dxdy} = $$ $$ \int\limits_{0}^{\pi/4}{sen(x)dx} = 1 – \frac{\sqrt{2}}{2} .$$

(b) f(x,y) = x \sqrt{y} e R é o domínio delimitado pelas retas x+2 = y, y = 0 e a parábola x = y^2 .

SOLUÇÃO: Neste caso é conveniente integrar primeiro para a variável x . Pois se quisermos integrar primeiro para a variável y , teríamos que dividir a região R em duas pela reta x =1 , além de chegarmos em integrais mais complicadas com esta escolha de integração.

Desta forma, nossa região R será dada por $$R: \left\{ \begin{array}{l}
y^2 \leq x \leq 2-y\\
0 \leq y \leq 1
\end{array} \right.  $$ conforme vemos pelo seu esboço:

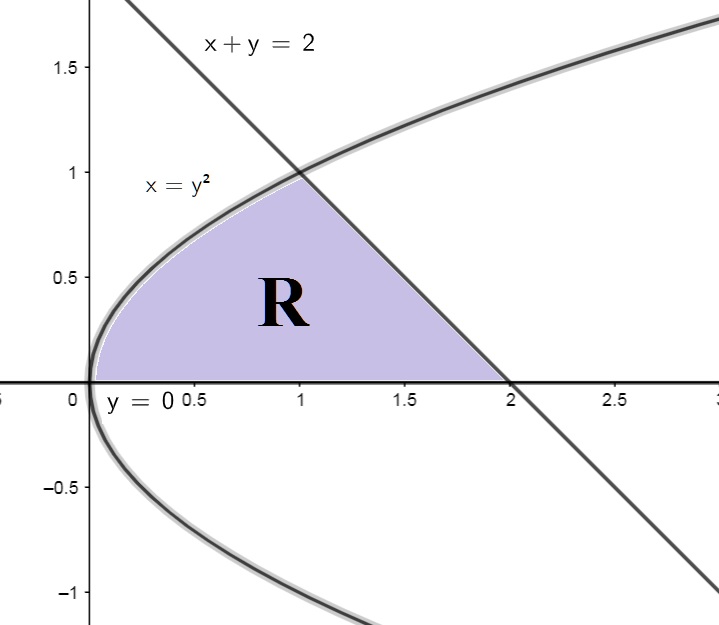
Assim, $$ \int\limits_{R} \int{x \sqrt{y}dxdy} = \int\limits_{0}^{1} \int\limits_{y^2}^{2-y}{x \sqrt{y}dxdy} = $$ $$\int\limits_{0}^{1}{\frac{\sqrt{y}}{2}\left[ (2-y)^2 – y^4 \right]dy} = \frac{676}{1155} .$$

2) Calcule $$\iint\limits_{R}(x+2y)dxdy,$$ onde R é região delimitada pelas parábolas y = 2x^2 e y = 1 +x^2.

SOLUÇÃO: As parábolas intersectam quando 2 x^2 = 1 + x^2 , ou seja, x^2 = 1 \leftrightarrow x = \pm 1. Note que a região R , ilustrada na figura abaixo pode ser escrita como $$ – 1 \leq x \leq 1 $$ $$2 x^2 \leq y \leq 1 +x^2.$$

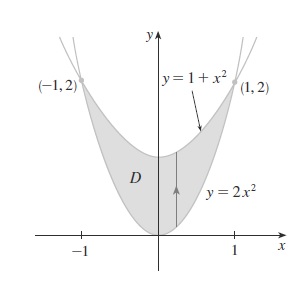
Agora, calculando a integral obtemos $$\iint\limits_{R}(x+2y)dxdy = \int\limits_{-1}^{1} \int\limits_{2x^2}^{1 + x^2}(x+2y)dxdy = \\ = \int\limits_{-1}^{1} \left[ xy + y^2 \right]_{2x^2}^{1 + x^2} =  \int\limits_{-1}^{1} \left[ -3x^4-x^3+2x^2+x+1) \right]dx = \\ = \left[ \frac{-3}{5} x^5 – \frac{1}{4} x^4 + \frac{2}{3} x^3 + \frac{1}{2} x^2 + x \right]_{-1}^{1} = \frac{32}{15} .$$

3) Calcule as Integrais Impróprias abaixo:

(a) \int_{0}^{ \infty} \int _{0}^{ \infty}{e^{-x-y}dxdy}

SOLUÇÃO: Observe que nesta integral imprópria estamos considerando todo o primeiro quadrante. Assim podemos estabelecer uma região R dada por $$R: \left\{ \begin{array}{l}
0 \leq x \leq M\\
0  \leq y \leq M
\end{array} \right.  $$ que é um quadrado de lado M no primeiro quadrante e com dois de seus lados sobre os eixos coordenados.

Com isso, quando fizermos M \rightarrow \infty iremos cobrir todo o primeiro quadrante e com isso, podemos calcular nossa integral dupla imprópria da seguinte maneira: $$ \int_{0}^{ \infty} \int _{0}^{ \infty}{e^{-x-y}dxdy} = \lim\limits_{M\rightarrow \infty } \int_{0}^{ M} \int _{0}^{M}{e^{-x-y}dxdy} = $$ $$ = \lim\limits_{M\rightarrow \infty } \left( – e^{-M} +1 \right)\int_{0}^{ M} {e^{-y}dy} = \lim\limits_{M\rightarrow \infty } \left( – e^{-M} +1 \right)^2 = 1.$$

(b) \int \int _{D}{x^2e^{-x^2-y^2}dxdy} , onde D: x \geq 0, y \geq 0.

SOLUÇÃO: Nossa região de integração é o primeiro quadrante como um todos inspirado pela mudança de variável que a própria função de integração pedirá, iremos preencher o primeiro quadrante com arcos de circunferência com ângulos de \pi / 2 .

Assim, podemos estabelecer uma região D dada por $$R: \left\{ \begin{array}{l}
0 \leq r \leq M\\
0  \leq \theta  \leq \pi /2
\end{array} \right.  $$ que é um quarto de círculo de raio M, centro na origem e todo contido no primeiro quadrante.

Com isso, quando fizermos M \rightarrow \infty iremos cobrir todo o primeiro quadrante e com isso, podemos calcular nossa integral dupla imprópria da seguinte maneira:

$$\int \int _{D}{x^2e^{-x^2-y^2}dxdy} = \lim\limits_{M\rightarrow \infty } \int_{0}^{ M} \int _{0}^{\pi /2}{r^3 e^{-r^2}cos^2 ( \theta) dr d \theta} = $$ $$ = \lim\limits_{M\rightarrow \infty } \int_{0}^{ M}{r^3 e^{-r^2}dr }\int _{0}^{\pi /2}{cos^2 ( \theta)  d \theta} = \frac{ \pi}{8} \lim\limits_{M\rightarrow \infty }{\left[ 1 – r^2 e^{-r^2} – e^{-r^2} \right]} = \frac{ \pi}{8}.$$

Leia Mais:

• Integrais Duplas | 1ª Lista de Exercícios Resolvidos
• Mudança de Variável em Integrais Duplas | Funções de Várias Variáveis
• As Integrais Triplas | Definição, Exemplos e Exercícios Resolvidos
• Mudança de Variável em Integrais Triplas | Coordenadas Cilíndricas e Esféricas
• Integrais Duplas Impróprias | Teoria e Exercícios Resolvidos.

Assista Nossas Duas Vídeo Aulas