O Guia Completo das Frações: Adição, Multiplicação, Divisão, Potenciação, Radiciação e Representação Decimal

Este artigo é um guia completo sobre o entendimento e a manipulação de frações e números decimais, essencial para estudantes e educadores. Exploramos os conceitos fundamentais, incluindo tipos de frações, propriedades, e técnicas de simplificação. Abordamos também a conversão entre frações e decimais, destacando métodos práticos para transformar representações fracionárias em decimais e vice-versa.

Introdução

As frações e os números decimais são componentes fundamentais da matemática, permeando desde problemas cotidianos até complexas teorias matemáticas. Este artigo serve como um guia abrangente para entender e utilizar frações e decimais de forma eficaz.

Este segmento é crucial para estudantes que precisam entender como diferentes representações numéricas interagem dentro da matemática. Além disso, oferecemos estratégias práticas para resolver problemas comuns e menos comuns envolvendo esses conceitos. Com este guia, os leitores poderão reforçar seu conhecimento matemático e aplicar esses conceitos em várias situações, promovendo uma maior fluência em matemática.

Frações

Os números racionais podem ser representados por um numeral em forma de fração ou razão \dfrac{a}{b} , sendo a e b números inteiros, com a condição de b ser diferente de zero. Todo número natural poderá ser representado por uma fração de denominador 1. Logo, é possível reunir tanto os números inteiros como os fracionários em um único conjunto, chamado conjunto dos números racionais \mathbb{Q} .

Para se representar numericamente uma ou mais partes de um inteiro, são necessários dois números naturais:

• o primeiro, indicando quantas partes de igual valor foram tomadas do inteiro ( a ).
• o segundo indicando em quantas partes de igual valor o inteiro-dividido ( b ).
• Chama-se de termos da fração ao conjunto formado pelo numerador e denominador.

Nesses novos símbolos \dfrac{a}{b} , \dfrac{1}{2} , \dfrac{5}{6} , \dfrac{3}{8} etc., o primeiro elemento ( a , 1, 5, 3,) chama-se numerador e o segundo elemento ( b , 2, 6, 8) denominador dos números fracionários ou das Frações.

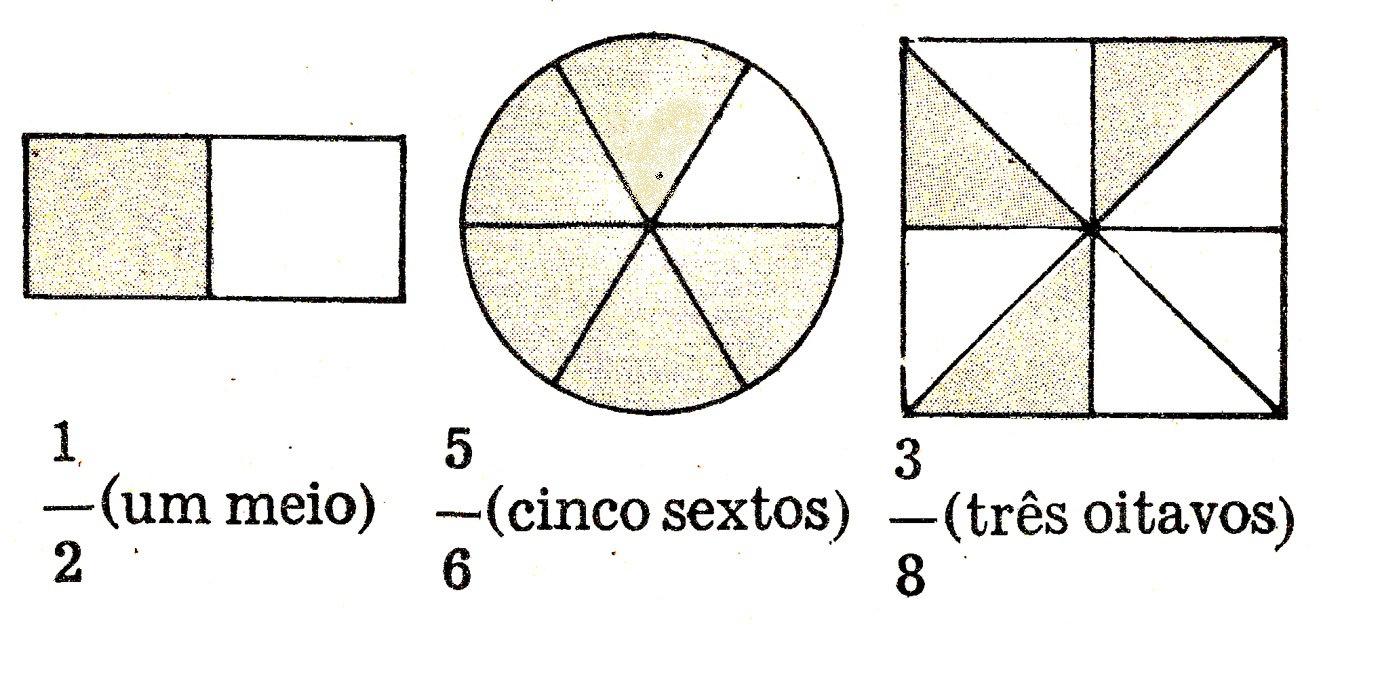
Tipos de Frações

• Fração própria- aquela cujo numerador é menor do que o denominador (representam quantidades menores que 1). Exemplos: \dfrac{1}{2} , \dfrac{5}{7} ;
• Fração imprópria — aquela cujo numerador é maior do que o denominador (representa quantidades maiores ou iguais a 1). Exempos: \dfrac{7}{5} , \dfrac{5}{3};
• Fração Decimal – quando o denominador for 10 ou uma potência de 10. Exemplos: \dfrac{2}{10} , \dfrac{1}{100} ;
• Fração aparente – quando o numerador for múltiplo do denominador. Exemplo: \frac{20}{4} = 5 .
• Fração ordinária – toda fração que tem denominador diferente de 10 ou de potência de 10. Exemplo: \frac{3}{9} ;
• Fração irredutível – são aquelas que não podem mais ser simplificadas. Exemplo: \frac{7}{8} (seus termos são primos entre si)

Observação: O nome das frações deriva do denominador. Por exemplo: \dfrac{1}{2} é chamada de um meio; \frac{1}{3} é chamada de um terço; \frac{3}{4} é chamada de três quartos; etc.

Simplificação das Frações

Para simplificar uma fração, desde que não possua termos primos entre si, basta dividir os dois termos pelo seu máximo divisor comum. Simplificar uma fração \dfrac{a}{b} significa transformá-la numa fração \dfrac{c}{d} de modo que c e d sejam primos entre si. Por exemplo: \dfrac{8}{12} simplifica para \dfrac{2}{3} quando divide-se o numerador e o denominador por 4.

Comparação de Frações

1) Classes de equivalência: \sim é o símbolo de equivalência nas frações. Classe de equivalência é o conjunto de todas as frações equivalentes a uma fração dada.

Por exemplo, a classe de equivalência de \dfrac{3}{1} é o conjunto $$ \frac{3}{1}, \frac{6}{2}, \frac{9}{3}, … \text{ diferentes numerais para representar }\frac{3}{1} $$

2) Comparação de frações: para comparar duas ou mais frações quaisquer, em primeiro lugar devemos transformá-las em frações equivalentes de mesmo denominador. Por exemplo: $$ \frac{3}{4}, \frac{2}{3}, \frac{1}{2} \Leftrightarrow \frac{9}{12}, \frac{8}{12} \text{e} \frac{6}{12}$$

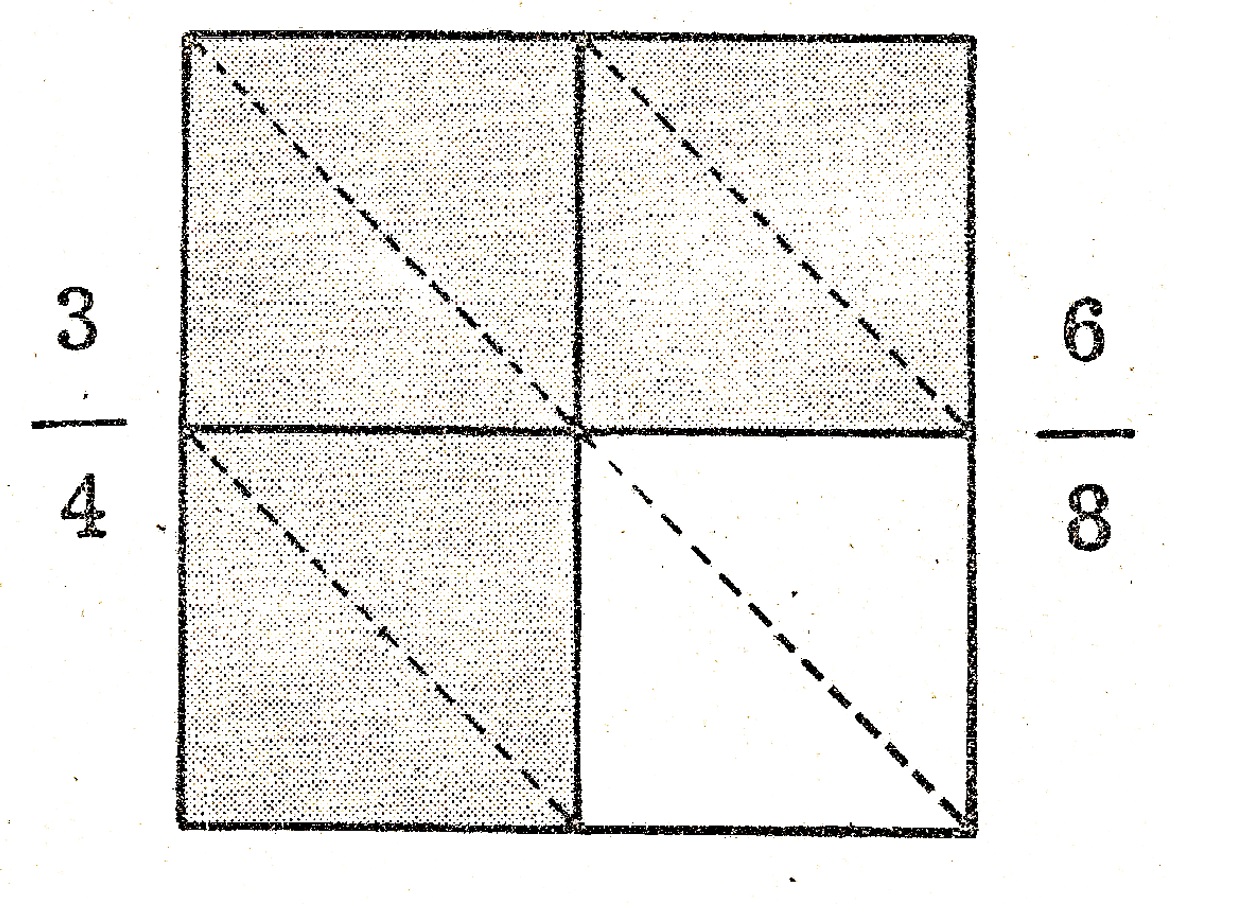
• Temos então que: Se duas frações têm o mesmo denominador, a maior é aquela que tiver o maior numerador. Por exemplo: $$\frac{9}{12} > \frac{8}{12} > \frac{6}{12}$$
• Temos que: Se duas frações têm o mesmo numerador, a maior é aquela que tiver o menor denominador. Por exemplo $$\frac{7}{2} > \frac{7}{5} > \frac{7}{8} .$$

Propriedade Fundamental

Multiplicando-se ou dividindo-se ambos os termos de uma fração por um número natural diferente de zero o valor desta fração não se altera, ou seja, obtem-se uma fração equivalente à fração dada. Por exemplo: $$ \frac{3}{4} \sim \frac{9}{12} \text{, pois }\frac{3 \cdot 3}{4 \cdot 3}  = \frac{9}{12}.$$

Propriedades das frações

• quando se multiplica o numerador de uma fração por um número m, toda fração fica multiplicada por m. Por exemplo: $$\frac{3}{4} \cdot 9 = \frac{27}{4};$$
• quando se divide o numerador de uma fração por um número diferente de zero toda fração fica dividida por esse número.Por exemplo: $$\frac{6}{8} \div 3 = \frac{2}{8};$$
• quando se multiplica o denominador de uma fração por um número diferente de zero toda fração fica dividida por esse número. Por exemplo: $$\frac{7}{13.2};$$
• quando se divide o denominador de uma fração por um número diferente de zero, toda fração fica multiplicada por esse número. Por exemplo: $$\frac{3}{4 \div 2}  = \frac{3}{2}.$$

Redução de frações a um mesmo denominador

Para se reduzir duas ou mais frações ao mesmo denominador comum temos que torná-las homogêneas. Homogêneas: quando duas frações têm denominadores iguais são ditas homogêneas caso contrário (denominadores diferentes) serão ditas heterogêneas.

Por exemplo: são frações heterogêneas; $$ \frac{5}{3}, \frac{1}{4}, \frac{1}{2}$$ enquanto $$ \frac{6}{12}, \frac{8}{12}, \frac{9}{12}$$ são homogêneas.

O problema é obter frações homogêneas equivalentes às frações dadas.

Desse modo:

1. determina-se o m.m.c. dos denominadores. Por exemplo, \dfrac{1}{2}, \dfrac{2}{3}, \dfrac{3}{4}, \dfrac{4}{5} são frações com denominadores 2, 3, 4 e 6, que possuem m.m.c dado por 12.
2. divide-se o m.m.c. achado (12) pelos denominadores das frações. O quociente obtido em cada caso deve ser multiplicado pelos termos da fração. Assim temos: para \dfrac{1}{2} (ex. acima): 1º passo m.m.c = 12; 2º passo 12 ÷ 2 = 6; 3º passo 6 .1 = 6, onde obtemos \dfrac{6}{12} \sim \dfrac{1}{2} . Ao final teremos $$ \frac{6}{12}, \frac{8}{12}, \frac{9}{12}, \frac{10}{12}.$$

Operação com Frações

Adição

Primeiro Caso (com denominadores iguais – frações homogêneas): Se as frações são homogêneas somam-se ou subtraem-se os numeradores conservando o mesmo denominador no resultado.

Por exemplo \dfrac{3}{7} + \dfrac{2}{7} = \dfrac{3+2}{7} = \dfrac{5}{7} .

Segundo Caso (as frações são heterogêneas): Nesse caso reduzem-se as frações ao menor denominador comum e procede-se como no primeiro caso.

Por exemplo: \dfrac{2}{3} + \dfrac{1}{4} = \dfrac{2 \cdot 4 + 1 \cdot 3}{4 \cdot 3} = \dfrac{8+3}{12} = \dfrac{11}{12}.

Terceiro Caso (inteiro e fração): Toma-se o número inteiro e escreve-se o mesmo sob a forma racional. Por exemplo, 2 = \dfrac{2}{1}. Teremos agora soma ou subtração de frações heterogêneas, procedendo então como no caso anterior.

Por exemplo: 2 + \dfrac{1}{4} = \dfrac{2}{1} + \dfrac{1}{4} = \dfrac{2 \cdot 4 + 1}{4} = \dfrac{9}{4}

O número expresso por: 2+ \dfrac{1}{4} (inteiro mais fração) é chamado número misto e costuma ser representado por 2 \frac{1}{4} que se lê: “dois inteiros e um quarto”. Assim pelo processo descrito acima podemos transformar o número misto em fração imprópria.

Quarto Caso (extração de inteiros de uma fração imprópria): Para se extrair os inteiros de uma fração imprópria, divide-se o numerador pelo denominador da mesma. O quociente indicará a parte inteira do número misto e o resto será o numerador da parte fracionária que conserva o denominador primitivo.

Por exemplo: \dfrac{9}{4} = \dfrac{4}{4} + \dfrac{4}{4} + 1 = 2 + \dfrac{1}{4} = 2 \dfrac{1}{4} .

Processo Prático:

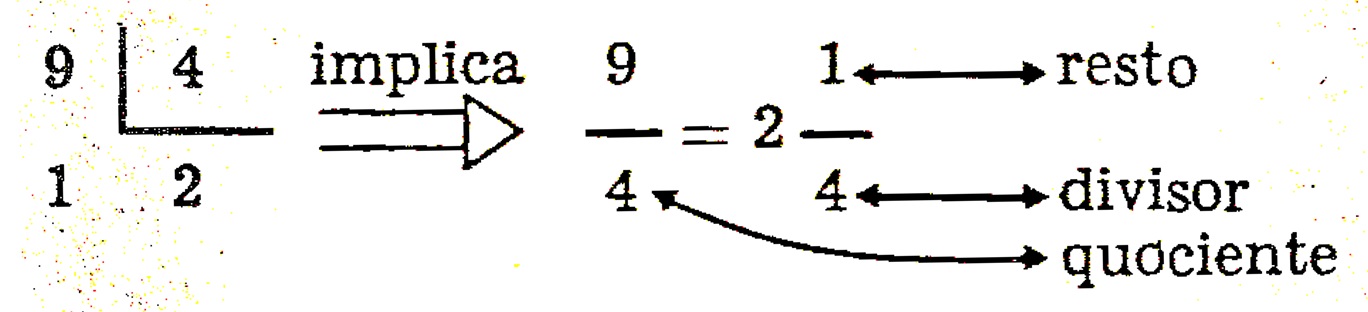
Multiplicação e Divisão

Multiplicação: o produto de duas frações é uma fração, onde o numerador é o produto dos numeradores e o denominador o produto dos denominadores das frações dadas. Antes de efetuar a multiplicação, simplifica-se por cancelamento.

Por exemplo, \dfrac{3}{5} \cdot \dfrac{4}{6} = \dfrac{3 \cdot 4}{5 \cdot 6} = \dfrac{12}{30} = \dfrac{2}{5}.

Divisão: Para se dividir uma primeira fração por uma segunda, multiplica-se a primeira pelo inverso da segunda.

Por exemplo: \dfrac{2}{3} \div \dfrac{2}{5} = \dfrac{2}{3} \cdot \dfrac{5}{2} = \dfrac{10}{6} = \dfrac{5}{3}.

Potenciação e Radiciação

A raiz n-ésima de uma fração é uma fração cujo numerador é a raiz n-ésima do numerador e cujo denominador é a raiz n-ésima do denominador da fração dada, ou seja, $$ \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a} }{ \sqrt[n]{b} }$$. Já a n-ésima potência de uma fração, é uma nova fração cujo numerador é a n-ésima potência da fração dada e o denominador é a n-ésima potência do antigo denominador. Ou seja, $$ \left( \frac{a}{b} \right)^n = \frac{a^n}{b^n}.$$

Por exemplo:

1. \sqrt{\dfrac{4}{100}} = \dfrac{\sqrt{4}}{\sqrt{100}} = \frac{2}{10}.
2. \left( \dfrac{2}{3} \right)^{3} = \dfrac{2^3}{3^3} = \dfrac{8}{27}.

Fração de Fração

Por exemplo, vamos \dfrac{2}{3} de \dfrac{5}{7}. Graficamente, temos que:

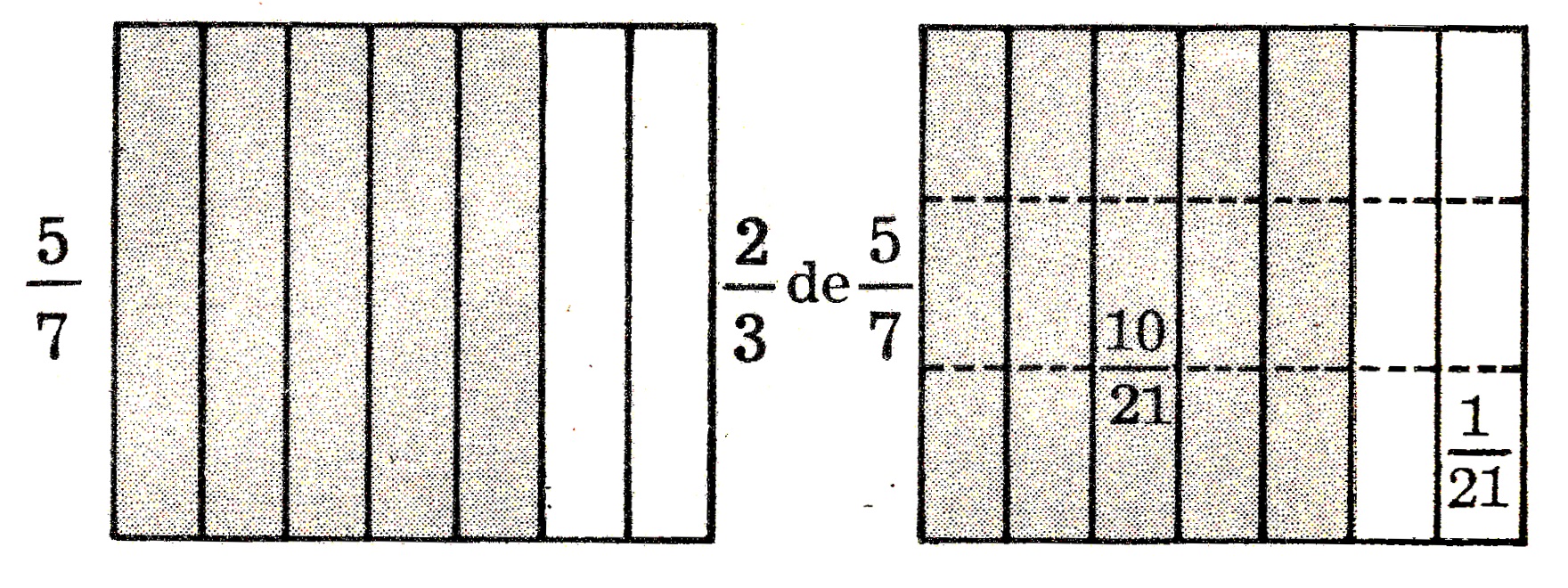
Na prática: \dfrac{2}{3} \text{ de }\dfrac{5}{7} = \dfrac{2}{3} \cdot \dfrac{5}{7} = \dfrac{10}{21}.

Expressões Fracionárias

A expressão fracionária representa um número. No cálculo deste número, deve-se respeitar a seguinte ordem:

1. operações de primeira ordem: potências e raízes.
2. operações de segunda ordem: multiplicações e divisões.
3. operações de terceira ordem: adições e subtrações.

Na expressão fracionária encontram-se agrupadas por meio de parênteses (); colchetes []; e chaves { }; as várias operações. Deve-se resolver em primeiro lugar as operações agrupadas nos parênteses a seguir as dos colchetes e por fim as das chaves.

Por exemplo, $$\left\{\left[\left(\sqrt{\frac{3}{4}}  \cdot \frac{4}{3} \right)^2 + \left(2 + \frac{1}{8}\right) \cdot \frac{4}{17} \right] + \frac{1}{3} \div 2\right\} \div \frac{3}{4} + 1 = $$ $$ \left\{\left[  \frac{3}{4} \cdot \frac{16}{9} + \frac{17}{8} \cdot \frac{4}{17} \right]  + \frac{1}{3} \cdot \frac{1}{2} \right\} \div \frac{3}{4} +1 = $$ $$ = \left\{ \left[ \frac{4}{3}+\frac{1}{2}  \right] + \frac{1}{6} \right\} \div \frac{3}{4} +1  = $$ $$ = \left\{ \frac{11}{6} + \frac{1}{6} \right\} \div \frac{3}{4} +1 = 3 \frac{2}{3}$$

Representação Decimal

A divisão do numerador pelo denominador de uma fração, pode ser exata ou não. Sendo exata, surge um número decimal exato. Por exemplo, \dfrac{6}{5} = 1.2 , como podemos ver na imagem abaixo

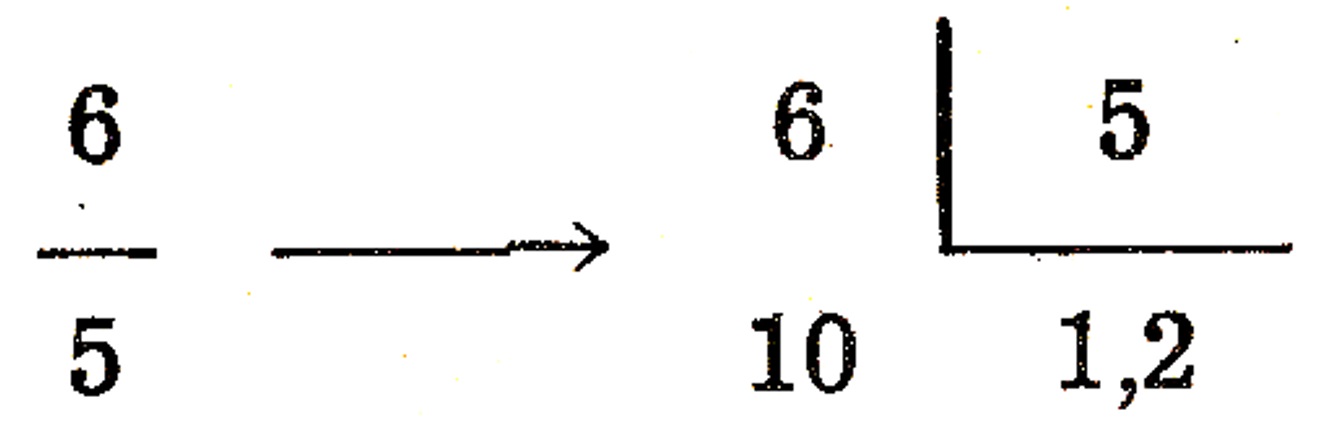
As Dízimas Periódicas

Não sendo exata, a divisão irá resultar numa sucessão numérica chamada “dízima periódica”, onde o resto da divisão se repete periodicamente e o quociente se prolonga indefinidamente. Por exemplo, \frac{1}{3} = 0,333333333... = 0, \overline{3}

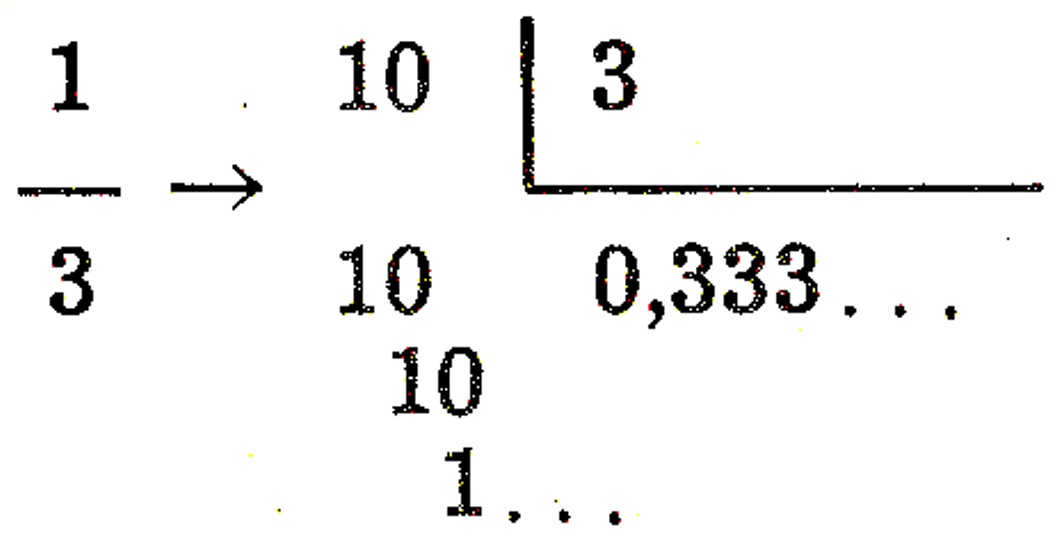
Nota: O traço horizontal sobre número, indica o período que se repete.

Tipos de Dízimas Periódicas

Encontramos dois tipos de dízimas periódicas:

1. SIMPLES – onde só aparece o período que se repete. Exemplo: 0,1414.
2. COMPOSTA – quando além da parte periódica aparece um número que não se repete, antecedendo o período. Exemplo: 0,573147314.

Passagem da representação fracionária para representação decimal:

Regra Prática: Considera-se o numerador e separam-se com uma vírgula, a começar pela direita, tantos algarismos quantos são os zeros do denominador (completando-se com zeros à esquerda, se necessário).

Por exemplo, \dfrac{33}{100} = 0.33; \dfrac{9}{1000} = 0.009, etc.

Passagem da representação decimal para a representação fracionária:

Regra prática: Escreve-se como numerador o número inteiro que se obtém suprimindo-se a vírgula, e como denominador, 1 (um) seguido de tantos zeros quantos forem os algarismos da parte decimal.

Por exemplo: 5.4 = \dfrac{54}{10}; 0.007 = \dfrac{7}{1000}.

Propriedade Fundamental das Representações Decimais

As representações decimais, que diferem apenas pelo número de zeros à direita de sua parte decimal, representam o mesmo número racional (são iguais). Por exemplo, 3.5 = 3.50 = 3.500 etc.

Operações entre decimais:

Adição:

Regras práticas: igualam-se as casas decimais (equivalente a homogeneizar frações heterogêneas). Em seguida, coloca-se vírgula debaixo de vírgula, equivalente a somar apenas as unidades de uma mesma ordem.

Por exemplo, 5,48 + 0,127 + 8,5 = 14,107

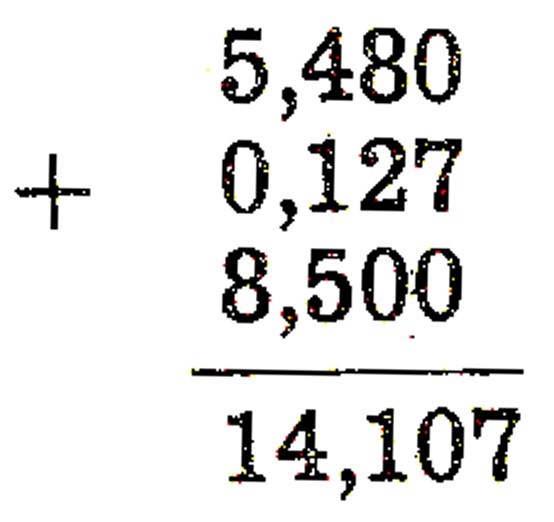
Subtração:

Utilizem-se as mesmas regras enunciadas para a adição, efetuando-se a subtração. Por exemplo: 18,40 - 6,31 = 12,09

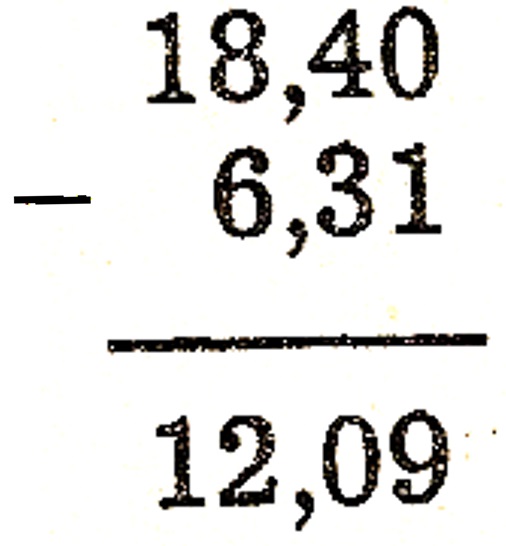
Multiplicação

Multiplicam-se os números decimais como se fossem números inteiros e dá-se ao produto tantas casas decimais quantas unidades somarem as casas do multiplicando e multiplicador.

Por exemplo, 0,73 \cdot 0,5 = 0,365, conforme a ilustração abaixo:

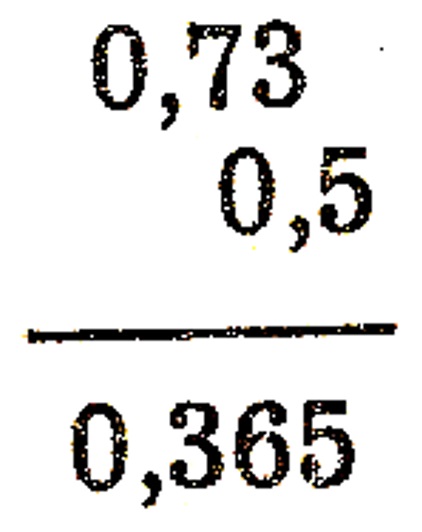
Divisão

Primeiro Caso – Divisão de inteiro por decimal: acerta-se as casas decimais. Elimina-se as vírgulas, efetua-se a divisão normalmente. No exemplo:
7,00 \div 0,35 = 20 procede-se da seguinte maneira:

Segundo Caso – Divisão de decimal por inteiro: acerta-se as ordens decimais. Acrescenta-se ao dividendo tantos zeros quantos forem necessários para tornar a divisão possível, sendo que o mesmo número de zeros deverá ser colocado no quociente, com a vírgula após o primeiro zero.

Por exemplo, vamos efeturar 0,350 \div 7 = 0,05

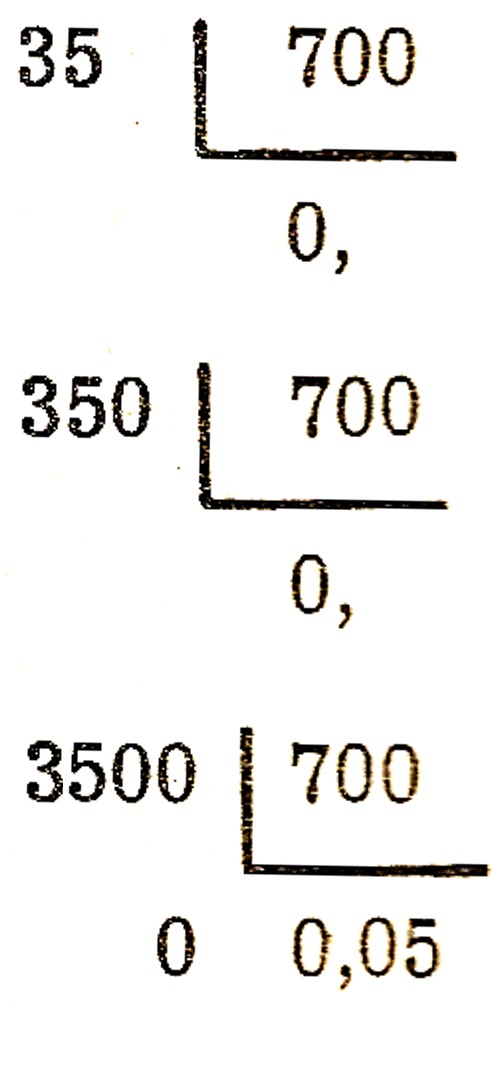
Conclusão:

Este guia detalhado ofereceu uma visão abrangente sobre frações e decimais, equipando os leitores com o conhecimento necessário para manipular esses conceitos matemáticos com confiança. Uma ferramenta essencial para qualquer estudante ou profissional que deseje aprofundar sua compreensão e habilidade em matemática.

Leia Mais:

• Múltiplos e Divisores, MDC e MMC, Números Primos e Critérios de Divisibilidade | Pré-Cálculo
• Entenda Tudo Sobre Números Irracionais: Exemplos e Curiosidades Históricas
• O que são Conjuntos Numéricos? Dos Naturais aos Complexos.
• Ajuste de Dados – Como fazer arredondamento de números?