Divisibilidade (Critérios, mmc e mdc) - Guia Completo Para Leigos

A divisibilidade é um conceito fundamental em matemática, essencial para a compreensão de números primos, múltiplos e divisores. Este artigo explora critérios de divisibilidade, técnicas de minimação e maximação, proporcionando uma abordagem técnica e objetiva ao tema.

Introdução

A divisibilidade é um dos conceitos fundamentais da matemática, essencial para a compreensão de estruturas numéricas mais complexas como números primos, múltiplos e divisores. Este artigo se propõe a explorar profundamente os critérios de divisibilidade, que determinam se um número é divisível por outro sem realizar a divisão propriamente dita.

Adicionalmente, discutiremos a importância dos números primos, que são os blocos construtores dos números naturais, e como eles se relacionam com os conceitos de múltiplos e divisores. Em um contexto mais avançado, abordaremos as técnicas de minimação e maximação, que são usadas para otimizar problemas envolvendo divisibilidade.

Este enfoque não apenas amplia o entendimento matemático, mas também fortalece as habilidades analíticas necessárias para resolver problemas complexos em diferentes áreas da ciência e engenharia. Portanto, nosso objetivo é oferecer um conteúdo rico e detalhado, que possa ser útil tanto para estudantes iniciantes quanto para profissionais buscando aprofundar seu conhecimento matemático.

Divisibilidade

Antes de entrarmos nos critérios e conceitos envolvendo a divisibilidade nos números reais é importante falar da operação de divisão.

A Divisão

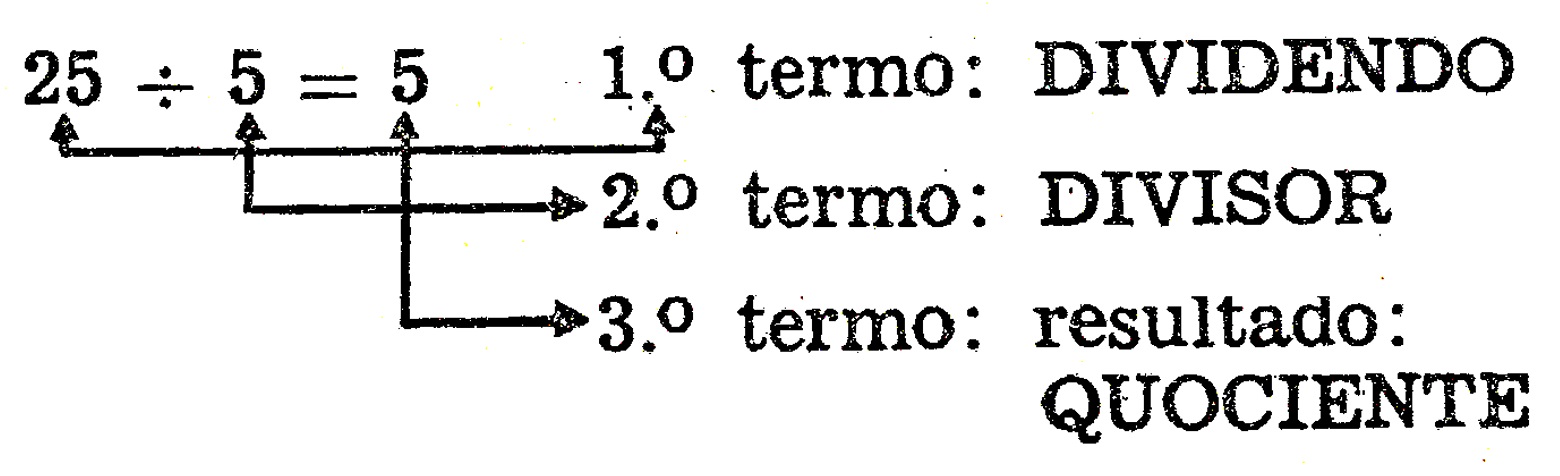
De forma simples e objetiva, a divisão poderia ser vista como a operação algébrica inversa da multiplicação. Uma divisão exata seria feita da sequinte maneira: dados dois números numa certa ordem, dividir o primeiro pelo segundo significa determinar um terceiro número, que multiplicado pelo segundo resulta o primeiro. Em simbologia matemática, podemos definir a divisão da seguinte maneira: $$ a \div b = c \Leftrightarrow c \times b = a .$$ Na operação de divisão o número $a$ é chamado de dividendo, o número $b$ de divisor e o número $c$ de quociente.

Por exemplo:

Porém, nem sempre é possível a divisão exata com dois números naturais quaisquer. Numa divisão não- exata temos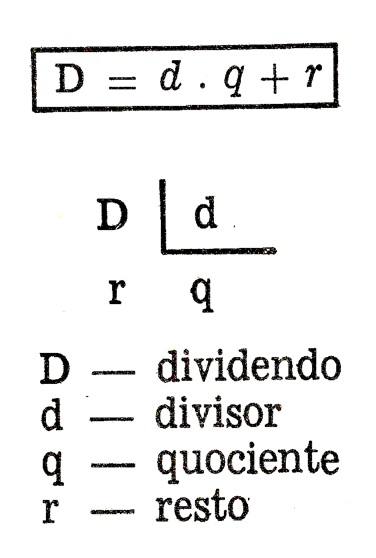

Algumas propriedades da divisão precisam ser registradas, pois serão cruciais no estudo do cálculo diferencial e integral:

Não é possível divisão por zero;
A divisão não possui propriedade da comutatividade. Por exemplo, $$ 8 \div 4 \neq 4 \div 8 ;$$
O elemento neutro da divisão é o número $1$ , ou seja, $a \div 1 = a .$ .

Múltiplos e Divisores

Entender múltiplos e divisores é vital para a análise de padrões numéricos e para a resolução de problemas envolvendo razões e proporções. Além disso, a capacidade de determinar rapidamente múltiplos e divisores pode ajudar em aplicações práticas como a organização de grupos ou a distribuição de recursos.

O múltiplo de um número é o produto deste número por outro número qualquer. Por exemplo, $10$ é múltiplo de $5$ , pois $5 \times 2 = 10.$

Algumas relaçãoes fundamentais entre múltiplos devem ser consideradas:

zero é o múltiplo de qualquer número, o único múltiplo de zero é o próprio zero;
Todo número é múltiplo de si mesmo e de $1$ ;
os mpultiplos de $2$ são chamados de números pares, sendo todos os outros números naturais ditos ímpares.
a soma ou a diferença de dois múltiplos de um número, são também múltiplos deste número.

O divisor de um número é todo número que divide exatamente aquele outro; diz-se então que o primeiro número é divísel pelo segundo, que é dito seu divisor.

Algumas relaçãoes fundamentais entre divisores também devem ser consideradas:

todo número é divisível por $1$ , isto é, $1$ é o menor divisor de qualquer número;
zero é divisível por qualquer número;
todo divisor de dois números é também divisor da soma e da diferença desses números. Por exemplo, $4$ é divisor de $24$ e de $8$ ; $4$ é o divisor de $24 + 8 = 32$ e de $24-8 = 16$ .

Números Primos

Os números se dividem em duas categorias:

Números primos: aqueles que somente são divisíveis por si mesmos e por um. São eles: $2,3,5,7,11,13,17,19,...$ .
Números compostos ou múltiplos: aqueles que eadmitem outros divisores além deles próprios e da unidade. Todo múltiplo admite pleo menos um divisor primo.

Os números primos são os blocos construtores dos números naturais. A identificação de números primos é crucial em várias áreas da matemática, incluindo a criptografia, onde a segurança dos dados muitas vezes depende da dificuldade de fatorar grandes números primos.

COMO RECONHECER UM NÚMERO PRIMO? O reconhecimento de um número primo se baseia na seguinte regra prática: divide-se o número dado pelos números da sucessão dos números primos, obtendo-se um quociente e um resto. Se o resto for diferente de zero até o instante em que o quociente se torna menor ou igual ao divisor, pode-se afirmar que o número é primo. Por exemplo, vamos verificar se $47$ é um número primo: $$ 47 = 3 \times 15 + 2 $$ $$ 47 = 5 \times 9 + 2 $$ $$ 47 = 7 \times 6 + 5. $$ Como $7 > 6$ , podemos garantir que $47$ é um número primo.

FATORAÇÃO OU DECOMPOSIÇÃO DE UM NÚMERO EM FATORES PRIMOS Todo número composto ou múltilo poderá ser decomposto de um só modo no produto de vários fatores primos. Por exemplo, \begin{eqnarray} 90 & = & 2 \times 45 \\ 90 & = & 2 \times 3 \times 15 \\ 90 & = & 2 \times 3 \times 3 \times 5 \end{eqnarray} Desta forma, podemos escrever $$ 90 = 2 \times 3^2 \times 5 .$$

Ou seja, para decompor um número em fatores primos divide-se inicialmente o número dado pelo seu menor divisor (que pode ser descoberto pelo critério de divisibilidade ou por tentativas); procede-se igualmente com o queociente obtido e assim por diantes até que se obtenha o quiciente igual a $1$. O número dado é o produto dos divisores empregados, que são todos primos.

Critérios de Divisibilidade

Como sabemos um número é ou não divisível por outro, quando o retso da divisão dor zero. Para alguns números, no entanto, existema regras práticas, chamadas critérios de divisibilidade, que tornam mais fácil a divisão do número.

Esses critérios são regras práticas que nos permitem determinar rapidamente se um número é divisível por outro sem realizar a divisão completa. Por exemplo, um número é divisível por 2 se seu último dígito for par, e por 5 se terminar em 0 ou 5. Estas regras, quando entendidas e aplicadas corretamente, podem significativamente acelerar a manipulação de grandes números e a solução de equações.

DIVISIBILIDADE POR 2 Todo número será divísivel por 2 quando seu último algarismo for um número par. Exemplos: 1020, 42, 54 e 45698 são todos números divisíveis por 2.

DIVISIBILIDADE POR 3 Todo número será divisível por 3 quando a soma dos valores absolutos de seus algarismos for divisível por 3. Por exemplo, o número 42.048 é divisível por 3, pois 4 + 2 + 0 +4 +8 = 18.

DIVISIBILIDADE POR 4 Todo número será divisível por 4, somente quando terminar por 00, ou seus dois últimos algarismos formem um número divisível por 4. Como exemplos temos os números 1436 e 1200 que são divisíveis por 4.

DIVISIBILIDADE POR 5 Todo número será será divisível por 5, somente quando terminar por 0 ou por 5. Números como 3.825 e 720 são ambos divisíveis por 5.

DIVISIBILIDADE POR 6 Todo número será divisível por 6 somente quando for divisível por 2 e 3 ao mesmo tempo. Exemplos: 510 é um número divisível por 6, pois é divisível por 2 e 3 ao mesmo tempo.

DIVISIBILIDADE POR 7 Um número é divisível por 7 se o dobro do seu último algarismo subtraído do número sem o último algarismo, resulta em um número divisível por 7. Se a diferença ainda é grande, repetimos o processo até verificar a divisão por 7. Por exemplo, 165928 é divisível por 7, pois, 16592 (que é o número sem o último algarismo) subtraído de 16 (que é o dobro de seu último algarismo) é igual a 16576. Este ainda é um número grande, e podemos repetir o processo: 1657 – 12 = 1645. Repetindo o processo mais uma vez, encontramos 164 – 10 = 154. Novamente: 15 – 8 = 7, que obviamente é divisível por 7. Portanto, 165928 é divisível por 7.

DIVISIBILIDADE POR 8 Todo número será divisível por 8 somente quando terminar em 000 (três zeros) ou for divisível por 8 o número formado pelos algarismos da unidade, dezena e centena. Exemplos: 1000 e 2480 são divisíveis por 8.

DIVISIBILIDADE POR 9 Todo número será divisível por 9, somente quando a soma dos valores absolutos dos seus algarismos for divisível por 9. Um exemplo é o número 6246, pois 6+2+4+8 = 18.

DIVISIBILIDADE POR 10 Todo número será divisível por 10, somente quando o número terminar em 0.

DIVISIBILIDADE POR 11 Um número será divisível por 11, somente quando forem iguais as somas dos valores absolutos dos algarismos de ordem ímpar e par ou a diferença entre maior e a menor soma for divisível por 11. Consideremos o número 82819, por exemplo. Este número é divisível por 11 porque a soma dos algarismos de ordem par é 1 + 2= 3 e a soma dos algarismos de ordem ímpar são 8+8+9 = 25, resultando que a diferença entre a maior e a menor soma é 25 – 3 = 22. Como 22 dividido por 11 é iguala a 2,podemos afirmar que 82819 é divisível por 11.

DIVISIBILIDADE POR 12 Todo número é divisível por 12 somente quando for divisível por 3 e 4 ao mesmo tempo. O número 348 é divisível por 12, pois é divisível por 3 e 4 ao mesmo tempo.

Maximação e Minimação

Estas técnicas são utilizadas para encontrar valores mínimos ou máximos que um conjunto de números pode assumir sob certas condições. Esta seção explora como esses conceitos são aplicados em problemas de otimização e em situações do dia a dia, ajudando a tomar decisões mais informadas e eficientes.

Maximação – Máximo Divisor Comum (m.d.c.)

Dados dois números (ou mais), chama-se divisor comum desses números todos número que for divisor de cada um deles ao mesmo tempo. Por exemplo, 1,2,4 e 8 são divisores de comuns de 40 e 16.

Apoie Nosso Trabalho:

Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697

MÁXIMO DIVISOR COMUM (M.D.C) Dados dois ou mais números que não poderão ser ao mesmo tempo nulos, chama-se máximo divisor comum desses números o maior de seus divisores. Por exemplo, 8 é o m.d.c entre 40 e 16.

É importante observar que:

A ordem dos números não altera o maior divisor comum entre eles, ou seja, $\text{m.d.c.} (a,b) = \text{m.d.c.} (b,a)$ ;
O maior divisor comum de dois números naturais é sempre um número natural.
Dois número que tem m.d.c igual a 1 são chamados de primos entre si.

DETERMINAÇÃO DO M.D.C.: É possível usar duas técnicas para encontrar o m.d.c. de um número:

Interseção: formam-se os conjuntos de divisores dos números em questão e o conjunto interseção entre eles, que será o conjunto de divisores comuns destes números. Daí, basta verificar qual o maior deles. Por exemplo: Para determinar o m.d.c. entre 20 e 12, temos que $$ \text{divisores de 12}: \{1,2,3,4,6,12\}$$ $$ \text{divisores de 20}: \{1,2,,4,5,10, 20\}$$ $$ \text{divisores comuns de 20 e 12}: \{1,2,4\}$$ $$\text{m.d.c.} = 4$$
Decomposição em fatores primos: Decompõe-se os números em fatores primos e tomam-se apenas os fatores comuns com seus menores expoentes. Vamos nomamente determinar o m.d.c. entre 20 e 12: $$ 20 = 2 \times 2 \times 5 = 2^2 \times 5$$ $$ 12 = 2 \times 2 \times 3 = 2^2 \times 3$$ $$ \text{m.d.c.} = 2^2 = 4.$$

Minimação – Mínimo Múltiplo Comum (m.m.c.)

Dados dois ou mais números, chama-se múltiplo comum desses números todo número que for múltiplo de cada um deles. Por exemplo, 0, 20, 40, 60 são todos múltiplos de 4 e 5.

MÍNIMO MÚLTIPLO COMUM (m.m.c.) Dados dois ou mais números diferentes de zero, chama-se mínimo múltiplo comum desses números o menor dentre os múltiplos comuns (excluindo o zero). Por exemplo, 20 é m.m.c. de 4 e 5.

É importante observar que:

A ordem dos números não altera o mínimo múltiplo comum entre eles, ou seja, $\text{m.m.c.} (a,b) = \text{m.m.c.} (b,a)$ ;
O mínimo múltiplo comum de dois números naturais é sempre um número natural.

DETERMINAÇÃO DO M.M.C.: É possível usar três técnicas para encontrar o m.m.c. de um número:

Interseção: formam-se os conjuntos de múltiplos dos números em questão e o conjunto interseção entre eles, que será o conjunto de múltiplos comuns destes números. Daí, basta verificar qual o menor deles. Por exemplo: Para determinar o m.m.c. entre 4 e 6, temos que $$ \text{múltiplos de 4}: \{0,4,8,12,16,20,24,28,…\}$$ $$ \text{múltiplos de 6}: \{0,6,12,18,24,30,…\}$$ $$ \text{múltiplos comuns de 4 e 6}: \{0,12,24,36,48,…\}$$ $$\text{m.m.c.} = 12$$
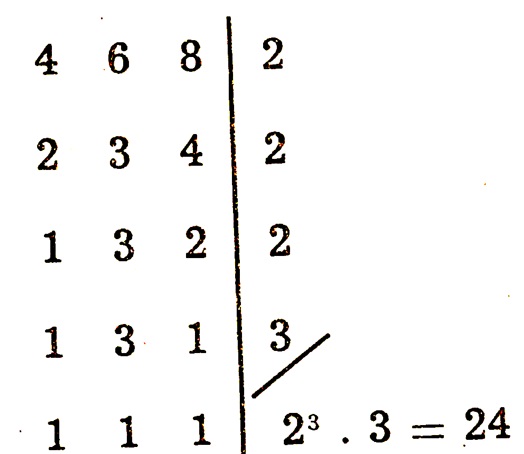
Decomposição em fatores primos: Decompõe-se os números em fatores primos e tomam-se todos os fatores comuns e não comuns com seus maiores expoentes. Vamos nomamente determinar o m.m.c. entre 4, 6 e 8: $$ 4 = 2 \times 2 = 2^2$$ $$ 6 = 2 \times 3 $$ $$8 = 2 \times 2 \times 2 = 2^3 $$ $$ \text{m.m.c.} = 2^3 \times 3 = 24.$$
Cálculo do m.m.c. a partir do m.d.c.: Vamos exemplificar esta forma novamente com o cálculo do m.m.c entre 4, 6 e 8. Basta calcular os divisores comuns de todos os números ao mesmo tempo, da seguinte maneira:

Conclusão:

Em resumo, o estudo da divisibilidade, complementado pelos critérios de divisibilidade, a análise de números primos, e a exploração de múltiplos e divisores, revela a beleza e a complexidade da matemática. As técnicas de minimação e maximação adicionam uma camada de profundidade ao aplicar estes conceitos em problemas práticos e teóricos. Espera-se que este artigo tenha oferecido uma visão abrangente e detalhada, incentivando o aprofundamento no estudo da matemática e melhorando a habilidade analítica dos leitores, essencial para o sucesso em muitas áreas científicas e tecnológicas.

Múltiplos e Divisores, MDC e MMC, Números Primos e Critérios de Divisibilidade | Pré-Cálculo

Introdução