Posições Relativas entre Planos e Retas no Espaço Tridimensional R³

Desbrave o mundo da geometria espacial e desvende os mistérios por trás dos ângulos entre planos e retas. Neste artigo, mergulhamos na análise precisa dessas relações, explorando fórmulas cruciais e condições geométricas. Prepare-se para uma jornada envolvente pela geometria analítica tridimensional.

Na vastidão do espaço tridimensional, a compreensão das relações entre planos é essencial. Este artigo desvenda os segredos dos ângulos entre essas superfícies, explorando fórmulas trigonométricas e condições de paralelismo.

Além disso, adentramos a interação entre retas e planos, desmistificando conceitos fundamentais da geometria analítica. Aprenda a calcular ângulos precisos e compreenda as condições de paralelismo e perpendicularismo.

Com exemplos práticos, esta exploração geométrica promete enriquecer sua compreensão do espaço tridimensional.

A Posição Relativa Entre Planos

No espaço, dois planos só podem ser paralelos ou concorrentes.

O cálculo do ângulo entre dois planos no espaço tridimensional é uma questão fundamental na geometria analítica.

Este artigo aborda a determinação precisa do ângulo entre dois planos, representados por equações lineares, através dos vetores normais associados a cada plano. A fórmula trigonométrica utilizada revela-se crucial para essa análise.

Além disso, são exploradas as condições de paralelismo e perpendicularismo entre planos, proporcionando uma compreensão abrangente das relações geométricas entre essas superfícies.

Para ilustrar tais conceitos, um exemplo prático é apresentado, destacando a aplicação prática dessas fórmulas no contexto da geometria espacial.

Como calcular o ângulo entre dois Planos?

Sejam os planos $$ \pi _1 : a_1 x + b_1 y +c_1 z + d_1 = 0 $$ e $$ \pi _2 : a_2 x + b_2 y +c_2 z + d_2 = 0 .$$ Então \vec{n_1} = (a_1 , b_1 , c_1 ) e \vec{n_2} = (a_2 , b_2 , c_2 ) são vetores normais a \pi _1 e \pi _2 , respectivamente, como mostrado na figura abaixo.

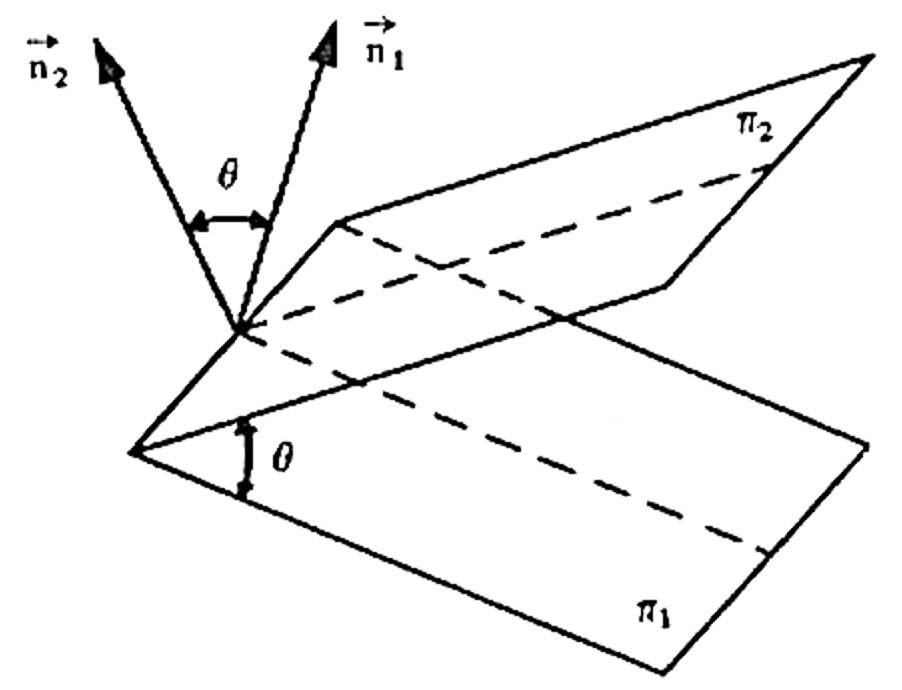
Chama-se ângulo de dois planos  \pi _1 e \pi _2 o menor ângulo que um vetor normal de \pi _1 forma com um vetor normal de \pi _2 . Sendo \theta este ângulo, tem-se $$ \text{cos}( \theta ) = \frac{|\vec{n_1} \cdot \vec{n_2}|}{|\vec{n_1} | |\vec{n_2}|}, \qquad \text{com } 0 \leq \theta \leq \frac{\pi}{2}.$$

EXEMPLO: Vamos determinar o ângulo entre os planos $$ \pi _1 : 2x-3y+5z-8 = 0 $$ e $$ \pi _2 :3x+2y+5z-4 = 0 .$$ Neste caso, os vetores \vec{n_1} = (2, -3,5) e \vec{n_2} = (3,2,5) são os normais a estes planos, respectivamente. Assim, $$ \text{cos}( \theta ) = \frac{|\vec{n_1} \cdot \vec{n_2}|}{|\vec{n_1} | |\vec{n_2}|} = \frac{|(2, -3,5) \cdot (3,2,5)|}{|(2, -3,5) | |(3,2,5)|} = \frac{| 25|}{\sqrt{38} \sqrt{38}} = \frac{25}{38}. $$ Logo: $$ \theta = \text{arc cos} \left( \frac{25}{38} \right) \Leftrightarrow \theta \approx 48º51′.$$

Condições de Paralelismo e Perpendicularismo de Dois Planos

Sejam os planos $$ \pi _1 : a_1 x + b_1 y +c_1 z + d_1 = 0 $$ e $$ \pi _2 : a_2 x + b_2 y +c_2 z + d_2 = 0 .$$ Então \vec{n_1} = (a_1 , b_1 , c_1 ) é perpendicular ao plano \pi _1 e \vec{n_2} = (a_2 , b_2 , c_2 ) perpendicular ao plano \pi _2 .

As condições de paralelismo e de perpendicularismo de dois planos são as mesmas de seus respectivos vetores normais, isto é:

I) Se   \pi _1 é paralelo a \pi _2 então  \vec{n _1} é paralelo a \vec{n _2} . Portanto, $$ \frac{a_2}{a_1} = \frac{b_2}{b_1} = \frac{c_2}{c_1} .$$

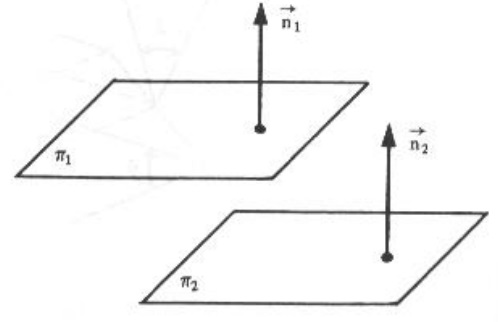
Se além das igualdades anteriores, se tiver também $$ \frac{a_2}{a_1} = \frac{b_2}{b_1} = \frac{c_2}{c_1} = \frac{d_2}{d_1},$$ os planos \pi _1 e \pi _2 serão coincidentes, porque, neste caso, a equação de \pi _1 é obtida de \pi _2 .

Em particular, se a_1 = a_2 , b_1 = b_2 , c_1 = c_2 e d_1 \neq d_2 , os planos também são paralelos.

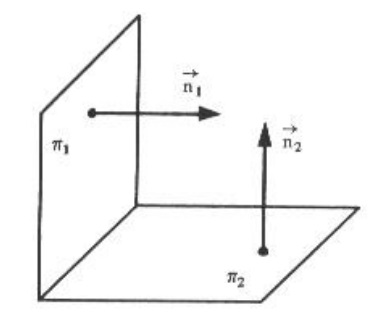
II) Se \pi _1 é perpendicular a \pi _2 então  \vec{n _1} é perpendicular a \vec{n _2} . Portanto, $$ a_1 a_2 + b_1 b_2 + c_1 c_2 = 0 .$$

EXEMPLO: O plano de equação x+3y+2z-6 = 0 é perpendicular ao vetor v=(1,3,2) e passa pelos pontos (6,0,0), (0,2,0) e (0,0,3).

A equação deste plano ainda pode ser escrita em sua forma vetorial utilizando dois vetores diretores (0,2,0) - (6,0,0) = (-6,2,0) e [/katex] (0,0,3) – (6,0,0) = (-6, 0, 3)[/katex] e o ponto (6,0,0) da seguinte maneira: $$(x,y,z) = (6,0,0)+\lambda (-6,2,0) + \gamma (-6,0,3)$$

Note que o vetor normal ao plano deve ser ortogonal a (-6,2,0) e (-6,0,3), simultaneamente.

Este vetor normal é encontrado pelo produto vetorial $$(-6,2,0) \wedge (-6,0,3) = \left|
\begin{array}{ccc}
i & j & k \\
-6 & 2 & 0\\
-6 & 0 & 3
\end{array}
\right| = (6,18,12) = 6(1,3,2),$$ ou seja, obtemos um vetor paralelo ao vetor normal original.

EXEMPLO: Considere dois planos x+2y-3z -10 = 0 e 2x+3y-4z+7 = 0.

Seus respectivos vetores normais são v_1 = (1,3,-3) e v_2 = (2,3,-4).

O ângulo entre os dois planos é dado por $$\cos{\theta} = \frac{|v_1 . v_2|}{\| v_1 \| \|v_2 \|} = \frac{20}{\sqrt{406}},$$ isto é, \theta = arccos\left( \frac{20}{\sqrt{406}} \right) \approx \frac{61}{50} \pi.

A Interseção de Dois Planos

Sejam os planos $$ \pi _1 : a_1 x + b_1 y +c_1 z + d_1 = 0 $$ e $$ \pi _2 : a_2 x + b_2 y +c_2 z + d_2 = 0 $$ não paralelos. Desta forma, eles possuem uma reta interseção Então a interseção entre estes planos será dada pela solução do sistema linear possível e indeterminado $$ r = \pi _1 \cup \pi _2 : \left\{ \begin{array}{lll}  a_1 x + b_1 y +c_1 z + d_1 = 0\\ a_2 x + b_2 y +c_2 z + d_2 = 0 \end{array} \right.$$

EXEMPLO: Vamos encontrar a reta interseção dos planos $$ \pi _1 : 5x-2y+z+7 = 0 $$ e $$ \pi _2 : 3x-3y+z+4 = 0 .$$ Para isso, precisamos solucionar o sistema linear $$ r = \pi _1 \cup \pi _2 : \left\{ \begin{array}{lll}  5x-2y+z+7 = 0 \\ 3x-3y+z+4 = 0 \end{array} \right.$$ que nos leva a $$ r : \left\{ \begin{array}{lll}  y = -2x-3  \\ z = -9x-13 \end{array} \right.$$ que são as equações reduzidas da reta interseção entre estes planos.

EXEMPLO: Vamos encontrar a reta interseção entre os planos de equações x+y+z-3 = 0 e x+y-z+1=0. Os pontos de interseção dos planos são aqueles onde as duas equações se igualam em suas soluções. Com isso, igualando as duas equações, obtemos, por eliminação de x+y , $$z-3 = -z +1 \Leftrightarrow z = 2. $$ Substituindo este valor nas equações dos planos encontramos $$x+y-1 = 0; \qquad z = 2 .$$ Ou seja, a reta interseção dos planos do enunciado é também a interseção dos planos x + y -1 = 0 e z = 2 . Fazendo x = t na primeira equação encontramos a reta de equação $$s:\left\{ \begin{array}{lll} x & = & t\\ y & = &1 -t\\ z & = & 2\\ \end{array} \right. ; \qquad t \in \mathbb{R} $$ que a reta que passa pelo ponto (0,1,2) na direção do vetor \vec{u} = (1,-1,0). .

Posição Relativa Entre Retas e Planos

No espaço, uma reta e um plano só podem ser paralelos ou concorrentes.

No domínio tridimensional, a interação entre retas e planos é fundamental para a compreensão da geometria espacial. Abaixo exploramos o ângulo entre uma reta e um plano, destacando a relação entre o vetor diretor da reta e o vetor normal do plano.

A fórmula do ângulo entre esses elementos é apresentada, proporcionando uma abordagem clara e precisa. Além disso, são delineadas as condições de paralelismo e perpendicularismo entre retas e planos, enriquecendo a compreensão das configurações geométricas possíveis.

Concluiremos com a análise da interseção entre uma reta e um plano, demonstrando a aplicação prática desses conceitos por meio de exemplos elucidativos.

Ângulo Entre uma Reta com um Plano

Seja uma reta r coma direção do vetor \vec{v} e um plano \pi , sendo \vec{n} um vetor normal a \pi .

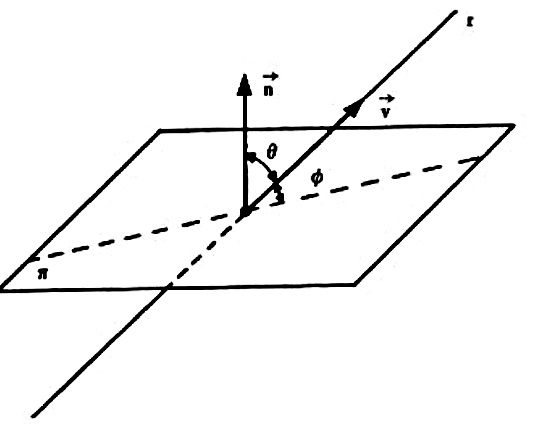
O ângulo \phi da reta r com o plano \pi é o complemento do ângulo \theta que a reta r forma com uma reta normal ao plano. Tendo em vista que $$\theta + \phi = \frac{ \pi }{2}$$ e, portanto, $$ \text{cos} ( \theta ) =  \text{sen} ( \phi ),$$ vem, de acordo com a fórmula do ângulo entre dois vetores $$ \text{sen}( \phi ) = \frac{|\vec{v} \cdot \vec{n}|}{|\vec{v} | |\vec{n}|}, \qquad \text{com } 0 \leq \phi \leq \frac{\pi}{2}.$$

EXEMPLO: Vamos determinar o ângulo que a reta $$ \left\{ \begin{array} x = 1 – 2t \\ y = -t \\ z =  3 + t \end{array} \right.$$ forma com o plano $$ \pi: x+y-5 = 0.$$ A reta r tema direção do vetor \vec{v} = (-2,-1,1) e \vec{n} = (1,1,0) é um vetor normal ao plano \pi . Daí, $$ \text{sen}( \phi ) = \frac{|(-2,-1,1) \cdot (1,1,0) |}{| (-2,-1,1) | | (1,1,0) |} = \frac{|-2-1+0}{\sqrt{4+1+1} \sqrt{1+1} } = \frac{|-3|}{\sqrt{6} \sqrt{2}} = \frac{\sqrt{3} }{2}$$ Portanto, $$ \phi = \text{arc sen} \left( \frac{\sqrt{3} }{2} \right) = \frac{\pi}{3}.$$

Condição de Paralelismo e Perpendicularismo entre Retas e Planos

Para a reta r e o plano \pi dados na seção anterior, temos:

I) Se r é paralelo a \pi , então \vec{v} é perpendicular a \vec{n} .

Observação: Uma reta estará contida em um plano se o seu vetor diretor for perpendicular ao vetor normal do plano e se um ponto A   pertencente à reta pertence também ao plano. Uma reta r está também contida num plano \pi se dois pontos A e  B pertencentes a r pertemcem a esse plano.

II) Se r é perpendicular a \pi , então \vec{v} é paralelo a \vec{n} .

EXEMPLO: Determine as equações paramétricas da reta que passa pela origem e é perpendicular ao plano de equação 2x-y+3z-6=0.

O vetor diretor da reta procurada é o vetor normal ao plano do enunciado. Desta forma, as equações paramétricas da reta que passa pela origem e é perpendicular ao plano é dada por $$\left\{ \begin{array}{lll}
x & = & 2t\\
y & = & -t\\
z & = & 3t\\
\end{array}
\right.$$

A Interseção de Reta com Plano

A interseção de uma reta com um plano, ambos não paralelos, será dada pelo ponto cujas coordenas são dadas pela solução do sistema linear formado pela equações do plano e da reta.

EXEMPLO: Vamos determinar o ponto de interseção entre a reta $$ r : \left\{ \begin{array}{lll}  y = 2x+3  \\ z = 3x-4 \end{array} \right.$$ com o plano $$ \pi : 3x + 5y -2z – 9 = 0 .$$ Para isso precisamos resolver o sitema linear $$\left\{ \begin{array}{lll}  y = 2x+3  \\ z = 3x-4 \\ 3x + 5y -2z – 9 = 0 \end{array} \right.$$ Resolvendo o sistema obtem-se $$ x= -2 \qquad y = -1 \qquad z = -10 .$$ Portanto, o ponto de interseção entre r e \pi é I(-2,-1,-10) .

EXEMPLO: Determine o ponto de interseção do plano de equação 2x-y-3z-4=0 com a reta que passa pelo ponto (0,1,-1), na direção do vetor (1,-2,1).

As equações paramétricas da reta do enunciado são dadas por $$\left\{ \begin{array}{lll}
x & = & t\\
y & = & 1 – 2t\\
z & = & -1 + t\\
\end{array}
\right.$$ O ponto de interseção do plano com a reta deve satisfazer às duas equações ao mesmo tempo. Assim, substituindo as equações paramétricas da reta na equação do plano obtemos $$2(t) – (1-2t)-3(-1+t) – 4 = 0 \Rightarrow t=2.$$ Logo, o ponto P(2,-3,1) é o ponto de interseção do plano e da reta.

Conclusão

Neste mergulho na geometria espacial, desvendamos os mistérios dos ângulos entre planos e retas. Com fórmulas precisas e exemplos práticos, a compreensão das relações geométricas no espaço tridimensional é enriquecida. Ao calcular ângulos e analisar interseções, ampliamos nossa perspectiva sobre a geometria analítica, tornando-a acessível e fascinante.

Leia Mais

• Estudo do Plano: Equações Geral e Vetorial – Geometria Analítica Espacial
• Retas no Espaço Euclidiano R³: Posiçoes Relativas Entre Retas
• As Equações da Reta no Espaço R³ – Geometria Analítica
• Vetores no R³: O Produto Misto e Duplo Produto Vetorial
• Vetores no R³: O Produto Vetorial e suas Interpretações Geométricas