Transformações e Suas Inversas | Funções Vetoriais de Várias Variáveis

Nesse artigo queremos apresentar uma introdução às funções vetoriais de várias variáveis, também chamadas de aplicações ou transformações.

Os termos aplicação e transformação são sinônimos de função e várias vezes são utilizadas para diferenciar as funções vetoriais de várias variáveis das demais.

Esta função associa cada n-upla ordenada (x_1,x_2, ..., x_n) \in A a um único vetor f(x_1,x_2, ..., x_n) \in \mathbb{R}^m, sendo m e n dois naturais diferentes de zero.

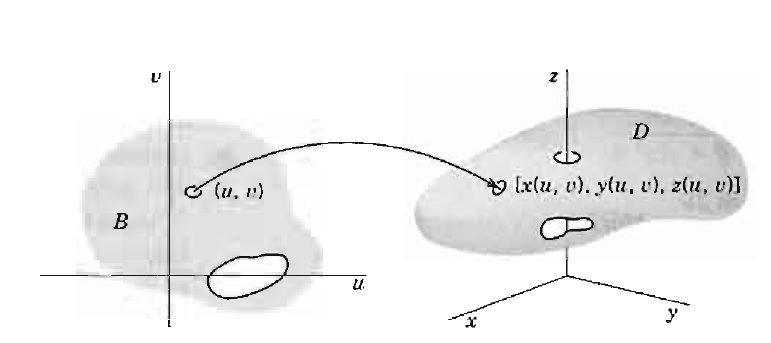
Uma função de n variáveis reais a valores vetoriais em \mathbb{R}^m é uma função f:A\rightarrow \mathbb{R}^m, onde A é um subconjunto não vazio de \mathbb{R}^n, denominado domínio de f.

O conjunto $$\left\{ f(x_1,x_2, …, x_n) \in \mathbb{R}^m; (x_1,x_2, …, x_n) \in A \right\}$$ é denominado imagem de f.

EXEMPLO

Seja f:\mathbb{R}^2 \rightarrow \mathbb{R}^3 dada por f(u,v) = (u, v, u^2 + v^2).

• Domínio de f: D_f = \mathbb{R}^2
• Imagem de f: Im_f = \left\{ (u, v, u^2 + v^2) \in \mathbb{R}^m; (u,v) \in \mathbb{R}^2 \right\}

É interessante observar que a imagem desta função descreve uma superfície no espaço que é um paraboloide.

EXEMPLO (Coordenadas Polares)

Considere a função \varphi: \mathbb{R} ^2 \rightarrow \mathbb{R} ^2 , tal que \varphi (\theta, \rho ) = ( \rho cos ( \theta), \rho sen ( \theta)) .

É interessante observar que, neste caso, as funções componentes são dadas por x( \rho, \theta) = \rho cos ( \theta) e y ( \rho, \theta) =  \rho sen ( \theta) e que esta transformação leva retas e retângulos do plano \theta 0 \rho em circunferências e círculos no plano x 0 y , respectivamente.

Aplicações Inversas

As aplicações biunívocas são muito importantes porque elas possuem inversas.

Seja f uma aplicação biunívoca com domínio D e imagem E. Dado um ponto Q em E existe um só ponto P em D tal que f(P) = Q . Esse ponto P é definido como a imagem de Q pela aplicação inversa f^{-1} (Q) = P . Portanto, $$ P = f^{-1} (Q)  \Leftrightarrow f(P) = Q .$$

EXEMPLO (Uma Transformação Linear)

Vamos considerar a transformação de f dada pelas equações $$ z = ax +by $$ $$ w = cx + dy, $$ onde a, b, c e d são constantes não nulas.

Esta aplicação tem a interessante propriedade de transformar restas em retas. De fato, os ponto P(x,y) de uma reta satisfazem equações paramétricas $$ x = mt + n, $$ $$ y = pt + q , $$ onde m, n, p e q são constantes e t é o parâmetro.

Substituindo-se essas equações  no primeiro sistema obtemos as coordenadas do ponto f(P) = Q na fora $$ z = (am+bp)t + (an +bq), $$ $$ w = (cm +dp)t + (cn + dq), $$ que são, novamente, equações paramétricas de uma reta.

Por essa razão, uma transformação dada por $$ f(x,y) = (ax +by ,  cx + dy) $$  é chamada transformação linear.

Finalmente, notamos que esta transformação será invertível se, e somente se, ad - bc \neq 0o .

Transformação Linear

Uma transformação \vec{f} é dita linear se satisfaz as propriedades:

1) \vec{f } (x + y) = \vec{f} (x) + \vec{f} (y) ;

2) \vec{ f } (t x) = t \vec{f} (x) ;

Estas equações exprimem a linearidade da aplicação \vec{f} como este conceito costuma ser definido na Álgebra Linear.

EXEMPLO

Uma aplicação linear f no espaço \mathbb{R} ^3 é dada pelas fórmulas de transformação $$u = a_1 x + b_1 y + c_1 z ,$$ $$v = a_2 x + b_2 y + c_2 z ,$$ $$ w = a_3 x + b_3 y + c_3 z .$$

É fácil verificar, como no exemplo anterior, que esta aplicação transforma retas em retas e planos em planos. Além disso, ela também satisfaz as propriedades de linearidade enunciadas acima.

EXEMPLO (A Transformação por Raios Vetores Recíprocos ou Transformação de Kelvin)

Vamos descrever a transformação por reflexão no círculo unitário, também chamada transformação por raios vetores recíprocos ou transformação de Kelvin. 

Dado P \neq \vec{0} , sua imagem f(P) é o ponto Q sobre o raio OP, satisfazendo a condição OQ = \dfrac{1}{OP} , como na figura abaixo:

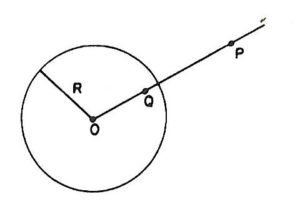O ponto Q é chamado a imagem refletida de P no círculo unitário. Essa transformação f leva o exterior do círculo unitário de centro na origem no seu interior e vice-versa.

Ela deixa invariantes os pontos da circunferência desse círculo (ou seja, f(P) = P se | P | =1 ) Além disso, f(P) \rightarrow 0 com P \rightarrow \infty e f(P) \rightarrow \infty com P \rightarrow 0 .

Vamos determinar as equações que relacionam x e y a u e v onde x e y são as coordenadas de P , e u e v as coordenadas de Q = f(P) . Para isso notamos que OQ = \kappa OP, \qquad \kappa >0 e OQ = \dfrac{1}{OP} . Então $$ u^2 + v^2 = \kappa ^2 (x^2 + y^2 )  $$ e $$ u^2 + v^2 = (x^2 + y^2)^{-1}, $$ donde obtemos \kappa = (x^2 + y^2)^{-1} , portanto, $$ u = \frac{x}{x^2 + y^2} $$ e $$ v = \frac{y}{x^2 + y^2} .$$

De modo análogo, a transformação inversa é dada por $$ x = \frac{u}{u^2 + v^2} $$ e $$ y = \frac{v}{u^2 + v^2} .$$

Note-se que f = f^{-1} , isto é, a transformação f coincide com sua inversa. Por essa razão os pontos P e Q = f(P) são ditos conjugados um do outro.

Leia Mais:

• Limite e Continuidade de Funções de Várias Variáveis Reais
• Funções de Variáveis Complexas | Limite e Continuidade
• Curvas | Limite e Continuidade de uma Função Vetorial
• Funções Vetoriais de Várias Variáveis | Transformações Lineares
• Funções Vetoriais de Várias Variáveis | O que são Campos Vetoriais?
• EFEITO BORBOLETA | Edward Lorenz e a Teoria do Caos
• Os Espaços Euclidianos R² e R³ | Cálculo de Várias Variáveis
• GRÁFICOS | Da Análise Estatística ao Mercado de Ações

Sugestão de Livros: