Rotacional de um Campo Vetorial | Definição e Interpretação Geométrica

Neste artigo queremos definir o rotacional de um campo vetorial. No cálculo vetorial, o rotacional é um operador vetorial que descreve a circulação infinitesimal de um campo vetorial no espaço euclidiano tridimensional e captura a ideia de como este campo pode ou não girar.

Seja A um subconjunto do \mathbb{R}^n e \vec{F} uma transformação de A em \mathbb{R}^n. Se para cada ponto de A o associarmos ao vetor \vec{F} iremos nos referir a \vec{F} como um campo vetorial.

No espaço \mathbb{R}^3, considere P(x,y,z) um ponto de um conjunto de pontos do espaço. Se para cada ponto P deste conjunto associarmos um vetor \vec{F}(P) = \vec{F}(x,y,z), então obtemos um campo vetorial para estes pontos e \vec{F}(x,y,z) é denominada função vetorial.

Em coordenadas cartesianas, $$\vec{F}(x,y,z) = F_1(x,y,z) i + F_2(x,y,z)j + F_3(x,y,z)k$$ onde i = (1,0,0), j = (0,1,0) e k = (0,0,1) e F_i : \mathbb{R}^3 \rightarrow \mathbb{R}

O Rotacional de um Campo Vetorial

Seja $$\vec{F}(x,y,z) = F_1(x,y,z) i + F_2(x,y,z)j + F_3(x,y,z)k$$ o campo vetorial definido em um aberto A do \mathbb{R}^3 e suponha que F_i admita derivadas parciais para i=1,2,3.

O rotacional de \vec{F}, que se denota por rot\vec{F}, é o campo vetorial definido em A e dado por $$rot \vec{F} = \left|
\begin{array}{ccc}
i & j & k \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\
F_1 & F_2 & F_3
\end{array}
\right| = \nabla \wedge \vec{F}$$ onde \nabla é o vetor gradiente.

EXEMPLO

Seja \vec{F}(x,y,z) = x y i + y z^2 j+ xz k o campo vetorial o qual queremos encontrar o rotacional. Daí, $$rot \vec{F} = \left|
\begin{array}{ccc}
i & j & k \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\
xy & y z^2 & xyz
\end{array}
\right| = -y \vec{i} – z \vec{j} – x \vec{k}.$$

No caso de um campo vetorial definido num aberto A do \mathbb{R}^2 dado por $$\vec{F}(x,y) = F_1(x,y) i + F_2(x,y)j$$ onde existam as derivadas parciais de F_1 e F_2 neste conjunto A, o rotacional é de \vec{F} é dado por

$$\left| \begin{array}{ccc}
i & j & k \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\
F_1 & F_2 & 0
\end{array}
\right| = \left( \frac{\partial F_2}{\partial x} – \frac{\partial F_1}{\partial y} \right)k$$

EXEMPLO

O campo vetorial \vec{F}(x,y) = -\omega y i + \omega xj onde \omega >0 possui rotacional dado por

$$rot \vec{F} = \left| \begin{array}{ccc}
i & j & k \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\
-\omega y & \omega x & 0
\end{array}
\right| = 2 \omega k$$

Campo vetorial irrotacional. 

Seja \vec{F}: \Omega \subset \mathbb{R} ^n \rightarrow \mathbb{R} ^n (n=2,3) um campo vetorial qualquer, dizemos que \vec{F} é irrotacional se, e somente se, rot \vec{F} = \vec{0}.

OBSERVAÇÃO: O rotacional de qualquer gradiente é o vetor nulo.

EXEMPLO

Considere o campo vetorial $$\vec{F}(x,y) = – \frac{\vec{r}}{\| r \|^2},$$ onde \vec{r}= xi + yj.

Vamos verificar se este campo vetorial é irrotacional. De fato, \vec{F} é irrotacional, pois

Temso que $$rot \vec{F} = \left| \begin{array}{ccc}
i & j & k \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\
-\frac{x}{x^2+y^2} & -\frac{y}{x^2+y^2} & 0
\end{array}
\right| = \frac{2xy}{x^2+y^2}-\frac{2xy}{x^2+y^2} = 0.$$

EXEMPLO

Considere o campo vetorial $$\vec{F}(x,y) = \left( -\frac{y}{x^2+y^2} ,\frac{x}{x^2+y^2} \right).$$

Em coordenadas polares o campo vetorial é dado por $$\vec{F}(r,\theta) = \frac{1}{r}\left( -\sin{\theta} ,\cos{\theta}\right)$$ e é representado por

Este campo vetorial está relacionado ao fenômeno de água escoando em um ralo.

Note que este campo vetorial não é irrotacional.

EXEMPLO

Considere um fluido em escoamento bidimensional com campo velocidade $$\vec{v}(x,y)=-y i + xj.$$

Calculando o rotacional deste campo vetorial temos que
$$rot \vec{v} (x,y) = \left[ \frac{\partial x}{\partial x} – \frac{\partial (-y)}{\partial y} \right]k = 2k \neq 0,$$ ou seja, \vec{v} não é irrotacional.

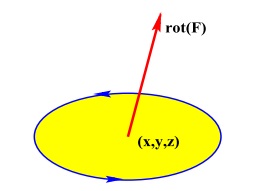
Interpretação geométrica do Rotacional

Para ilustrar uma interpretação do rotacional de um campo vetorial \vec{F}, considere que este campo vetorial é o campo de velocidade de um fluido e consideramos uma partícula situada no ponto (x,y,z).

As partículas situadas numa vizinhança deste ponto, tendem a rodar ao redor do eixo formado pelo vetor rot{\vec{F}} e o comprimento deste vetor representa a velocidade com que as partículas se movem ao redor deste eixo.

Se rot{\vec{F}} = \vec{0} então o fluído está livre de rotações na vizinha do ponto (x,y,z).

Listas de Exercícios Resolvidos

• Campos Vetoriais | 1ª Lista de Exercícios Resolvidos

Leia Mais:

• Campos Vetoriais Conservativos e Potencial
• Campo Vetorial | O que são as Curvas de Fluxo ou Curvas Integrais?
  
• O Rotacional de um Campo Vetorial | Definição e Interpretação Geométrica
• O Divergente de um Campo Vetorial | Definição e Interpretação
• Integral de Linha de 1ª e 2ª Espécies, e o Teorema de Green no Plano

Video-Aula Sobre Rotacional: