O que são Funções Pares e Funções Ímpares? | Pré-Cálculo

Uma função g(x) é dita par de g(-x)=g(x), para todo x. Por outro lado, se g(-x)=-g(x), para todo x, então g é dita ímpar. Por exemplo, a função f(x) = \cos{(n\pi x)}é par e g(x) = \sin{(n\pi x)} é ímpar. É importante ressaltar que a maior parte das funções são aquelas conhecidas como funções nem par nem ímpar.

Como exemplos imediatos podemos afirmar que

1. f(x)=x^2 é par;
2. a função identidade I(x)=x é ímpar;
3. f(x) = 2x -x^2 não é nem par nem ímpar.

O Gráfico de uma Função Par e de uma Função Ímpar

O gráfico de uma função par é sempre simétrico em relação ao eixo y . Se tomarmos, por exemplo, f(x) = x^2 , que é uma função par, podemos ver que, de fato, existe uma simetria em relação ao seu gráfico no eixo das ordenadas:

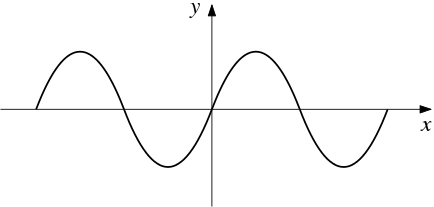
A curva que representa o gráfico de uma função ímpar é simétrica em relação à origem do plano cartesiano. Ilustramos abaixo o gráfico da função f(x) = sen(x) , a qual é uma função ímpar. Além disso, pode-se notar a simetria em relação ao ponto (0,0).

Propriedades das Funções Pares e Ímpares

Pode-se mostrar facilmente, pela definição, que a soma de duas funções pares é uma função par. Além disso, o produto de duas funções pares também é uma função par. Agora, usando a definição de função ímpar, podemos compreender que a soma de duas funções ímpares é uma função ímpar. Porém, o produto de duas funções ímpares é uma função par.

Ou seja, o produto h = g.f de uma função ímpar g por uma função par f resulta em uma função ímpar. De fato, $$h(-x) = g(-x).f(-x) = -g(x).f(x) = -h(x).$$

UMA PROPRIEDADE DA INTEGRAL DE FUNÇÕES REAIS

Uma propriedade interessante das funções pares e ímpares é que se g(x) é uma função par, então $$\int \limits _{-\pi}^{\pi}{g(x) dx} = 2\int \limits _{0}^{\pi}{g(x) dx},$$ mas se g(x) é uma função ímpar, então $$\int \limits _{- \pi }^{\pi}{g(x) dx} = 0.$$

Exercícios Resolvidos Sobre Funções Pares e Ímpares:

Classifique cada uma das funções abaixo em par, ímpar, ou nem par nem ímpar.

(1) f(x) = -2 , se -3 < x < 0; f(x) = 2 , se 0 < x < 3 ; e  f(x+6)  =  f(x)  

Pelo gráfico abaixo podemos ver que f(-x) = - f(x) , de modo que a função é ímpar.

(2) f(x) = cos(x) , se 0 < x < \pi ; f(x) = 0 , se \pi < x < 2 \pi ; e  f(x+ 2 \pi)  =  f(x)  

Pelo gráfico abaixo, podemos ver que a função é nem par nem ímpar, apesar da função cosseno ser uma função par.

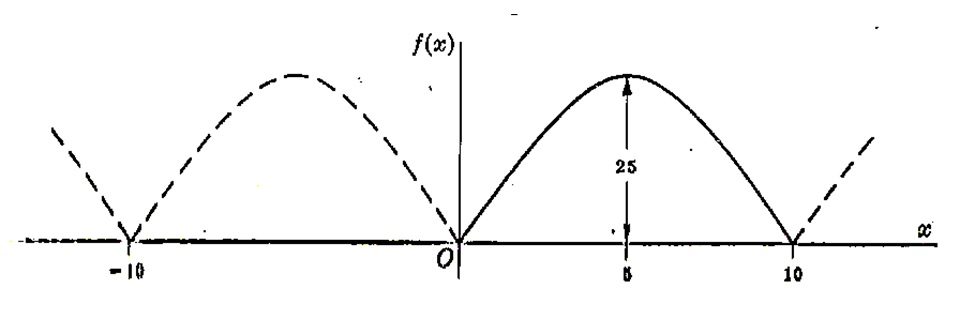
(3) f(x) = x(10-x) , se 0 < x < 10; e  f(x+10)  =  f(x)  

Pela figura abaixo, podemos ver que a função é par.

Leia Mais:

• O Jogo do Par ou Ímpar das Funções Reais
• O Que São Funções Periódicas? Definição e Exemplos.
• A Função Erro de Gauss ou Integral de Probabilidade
• Função Gama | Fatorial Generalizado e Gama Incompleta
• Função de Heaviside ou Degrau Unitário
• Funções de Variáveis Complexas | Uma Introdução.