Nos processos de obtenção de soluções de problemas de contorno surgem frequentemente funções especiais, como a função gama, a função erro de Gauss ou a função beta. Todas estas já estudadas anteriormente em seus respectivos artigos. Neste artigo queremos explorar algumas delas como a exponencial integral, o seno e o cosseno integral, bem como o seno e o cosseno integral de Fresnel.
A Função Beta
A função beta, denotada por B(m,n), foi estudada pela primeira vez pelos matemáticos Euler e Legendre, sendo definida por $$B(m,n) = \int_{0}^{1}{x^{m-1}(1-x)^{n-1} dx} \tag{1}$$ e convergente para m>0, n>0 . Esta função beta está associada com a função gama como segue: $$B(m,n) = \frac{\Gamma (m) \Gamma (n)}{\Gamma (m+n)},$$ onde $$ \Gamma (x) = \int_{0}^{ \infty}{t^{x-1}e^{-t} dt}.$$
A Função Gama
A função Gama é definida por $$ \Gamma (x) = \int_{0}^{ \infty}{t^{x-1}e^{-t} dt}.$$ A convergência desta integral requer x-1 > -1 , ou seja, x >0 . A relação de recorrência $$\Gamma (x+1) = x \Gamma (x),$$ pode ser obtida à partir à partir desta definição usando a técnica de integração por partes.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
A função Gama é frequentemente chamada de fatorial generalizado: para todo real \alpha > -1 definimos o fatorial de \alpha por $$ \alpha ! = \Gamma (\alpha +1) . $$
A Função Erro de Gauss
A Função Erro de Gauss, denotadas por erf(x) e erfc(x) desempenha um papel relvante em muitas aplicações envolvendo Transformadas Integrais, como a Transformada de Fourier e a Transformada de Laplace. Estas funções foram objetos de estudo de matemáticos como De Moivre (1718-1733) e Laplace (1774), onde foi expressa através da integral $$\int{e^{-x^{2}}dx}.$$
A função erro, denotada por erf(x) , é $$ erf(x) = \frac{2}{\sqrt{ \pi }} \int_{0}^{x}{e^{-u^2} du}.$$ A função erro complementar se define em termos da função erro: $$erfc(x) = 1 – erf(x).$$
A Função Exponencial Integral
Em matemática, a integral exponencial Ei é uma função especial no plano complexo. Ela é definida como uma integral definida particular da razão entre uma função exponencial e seu argumento. Para valores reais diferentes de zero de x , a integral exponencial Ei( x ) é definida como $$ Ei(x) = \int_{x}^{\infty}{\frac{e^{-u}}{u}du} = \int_{- \infty}^{x}{\frac{e^{-u}}{u}du}.$$
O algoritmo de Risch mostra que Ei não é uma função elementar. A definição acima pode ser usada para valores positivos de x , mas a integral deve ser entendida em termos do valor principal de Cauchy devido à singularidade do integrando em zero.
As Funções Seno e o Cosseno Integral
A função seno-integral é a função real Si : \mathbb{R} \rightarrow \mathbb{R} definido como: $$ Si (x) = \int_{0}^{x}{\frac{sen(u)}{u}du} = \frac{\pi}{2} – \int_{x}^{\infty}{\frac{sen(u)}{u}du}.$$ A função cosseno-integral é a função real Ci : \mathbb{R^{+}} \rightarrow \mathbb{R} definido como: $$ Ci (x) = \int_{x}^{\infty}{\frac{cos(u)}{u}du}.$$ Junto com a função exponencial integral, as funções seno e cosseno integral foram usadas por Schölmilch para expressar os valores de várias integrais mais complicadas.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
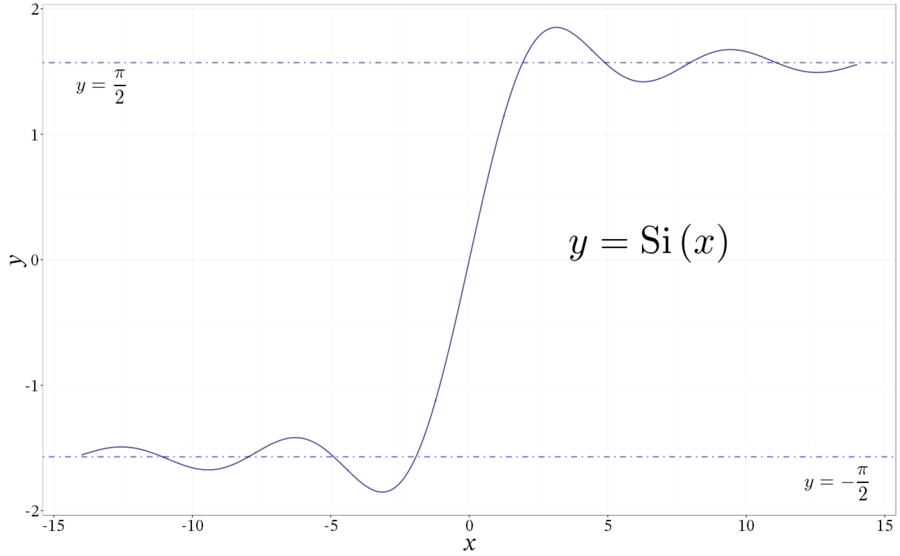 Gráfico da função seno integral
Gráfico da função seno integral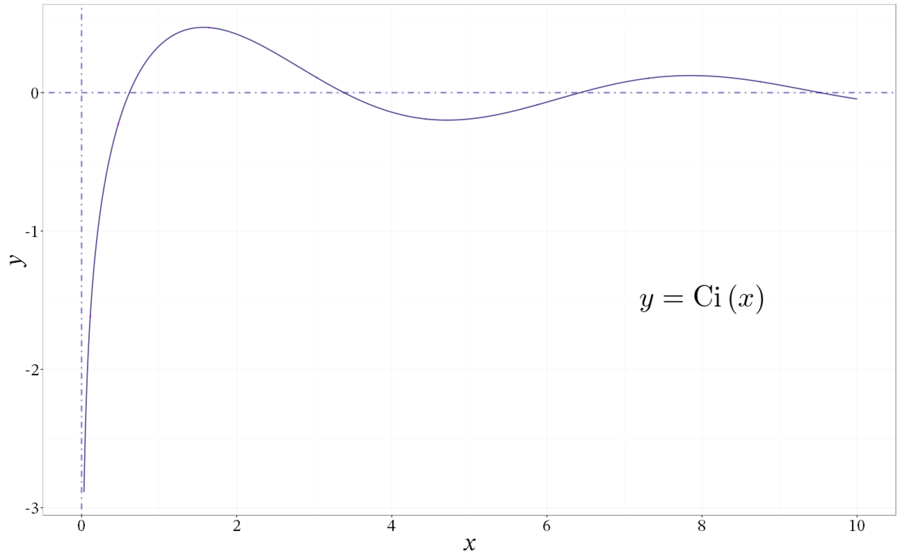 Gráfico da função cosseno integral
Gráfico da função cosseno integral
As Funções Seno e o Cosseno integral de Fresnel.
Existem várias definições ligeiramente diferentes das integrais de Fresnel. Em física, as integrais de Fresnel denotadas por S(x) e C(x) são mais frequentemente definidas por $$S(x) = \sqrt{\frac{2}{\pi}} \int_{0}^{x}{sen \left( u^2 \right) du} = 1 – \sqrt{\frac{2}{\pi}} \int_{x}^{ \infty}{sen \left( u^2 \right) du}$$ $$C(x) = \sqrt{\frac{2}{\pi}} \int_{0}^{x}{cos \left( u^2 \right) du} = 1 – \sqrt{\frac{2}{\pi}} \int_{x}^{ \infty}{cos \left( u^2 \right) du}$$
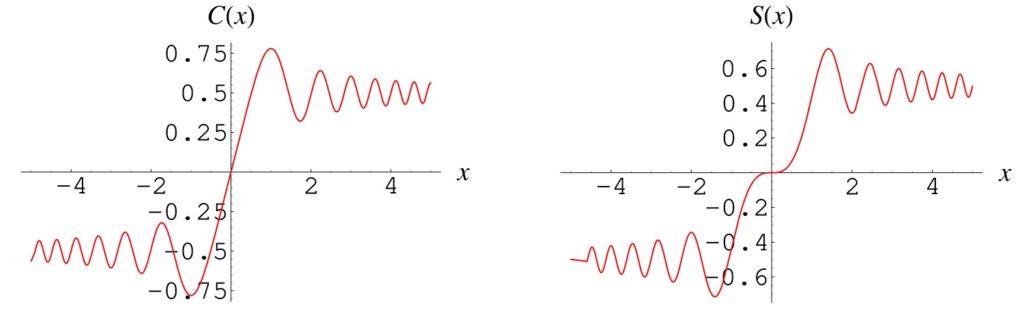 Funções Seno e Cosseno Integral de Fresnel
Funções Seno e Cosseno Integral de Fresnel


