Uma função de duas variáveis reais a valores reais é uma função f: A \subset \mathbb{R} ^2\rightarrow \mathbb{R}. Uma função desta forma associa, a cada par (x,y) \in A, um único número f(x,y) \in \mathbb{R}. O conjunto A é chamado de domínio de f e será indicado por D_f. O conjunto $$Im_f = \left\{ f(x,y) \in \mathbb{R}/ (x,y) \in D_f \right \}$$ é a imagem de f.
Este tipo de função aparece em aplicações de diferentes áreas de conhecimento, como em circuitos elétricos, otimização de volumes e modelos econômicos.Campos Escalares, ou Funções de Várias Variáveis a Valores Vetoriais, em geral são funções na forma f: A \subset \mathbb{R} ^n\rightarrow \mathbb{R}, que associa a cada n-upla de \mathbb{R} ^n um escalar.
Abaixo vamos apresentar exemplos de funções com domínio no \mathbb{R} ^2 simplesmente pela facilidade em estabelecer gráficos e representações do domínio, e também por serem as funções que mais aparecem em aplicações de engenharia, por exemplo.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
EXEMPLO
Considere a função $$f(x,y) = \frac{x+y}{x-y}$$
Seu gráfico pode ser dado por:
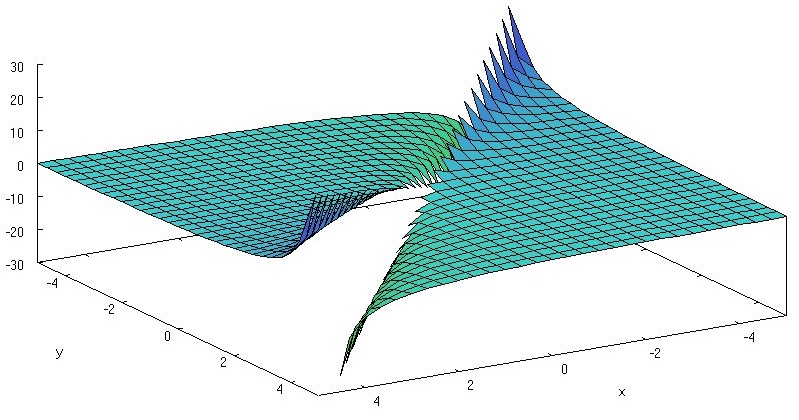 Gráfico da função f(x,y) = (x+y)/(x-y)
Gráfico da função f(x,y) = (x+y)/(x-y)
Neste caso, temos que:
- D_f= \left\{ (x,y) \in \mathbb{R}^2 ; x\neq y \right\} é o domínio desta função, ou seja, todos os pares(x,y) do \mathbb{R} ^2, tais que x \neq y
- f(2,3)=\frac{2+3}{2-3}=-5
EXEMPLO
Represente graficamente o domínio da função $$f(x,y) = \sqrt{y-x}+\sqrt{1-y}$$
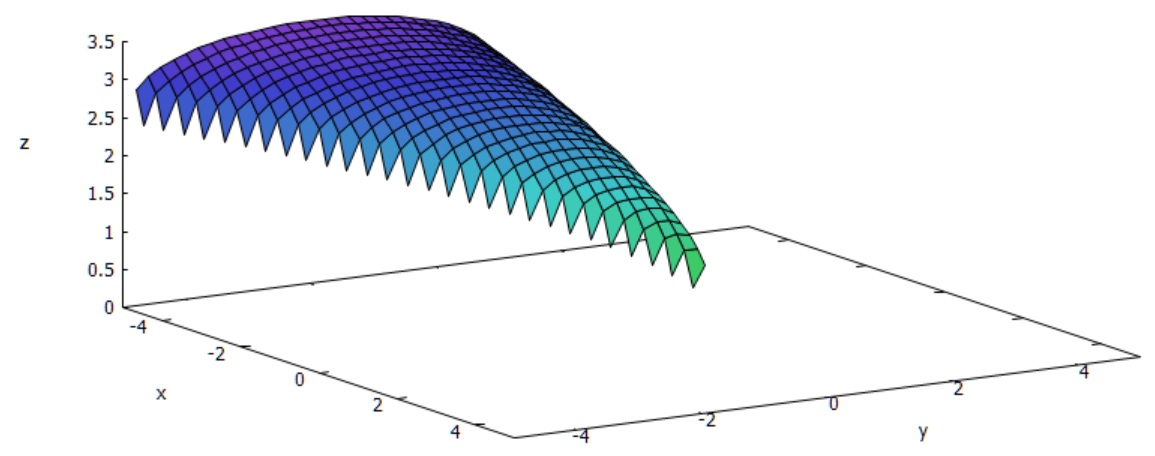
Temos que:
- y-x\geq 0 \Leftrightarrow y \geq x.
- 1-y\geq 0 \Leftrightarrow 1 \geq y.
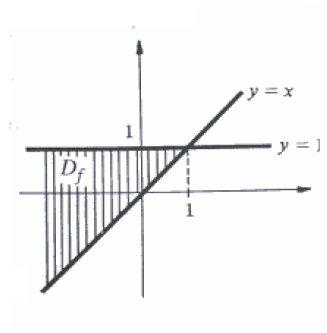
Portanto, D_f = \left\{ (x,y) \in \mathbb{R} ^2 ; y\geq x \;\;e\;\; y\leq 1 \right\}.
A representação deste domínio é dada por:
EXEMPLO
Toda função f: \mathbb{R}^2 \rightarrow \mathbb{R} da forma $$f(x,y)=ax+by$$ com a,b \in \mathbb{R} é denominada função linear e, em geral, estas funções determinam planos.
EXEMPLO
Represente graficamente o domínio da função w=f(u,v), dada por $$u^2 + v^2 +w^2=1,\;\;\;w\geq 0$$
Temos que,
$$u^2 + v^2 +w^2=1,\;\;\;w\geq 0 \Rightarrow w = \sqrt{1-u^2-v^2}.$$
Assim, nossa função é dada por $$w = \sqrt{1-u^2-v^2}.$$
Logo, para que w esteja bem definida precisamos que $$1-u^2-v^2 \geq 0 \Rightarrow u^2+v^2\leq 1$$
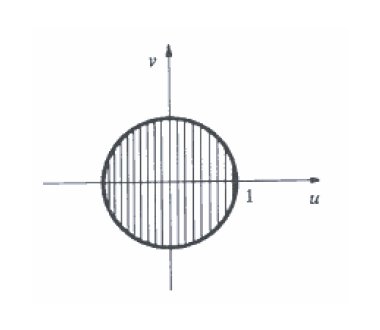 Representação gráfica do domínio da função w=f(u,v), dada implicitamente por u²+v²+w² = 1
Representação gráfica do domínio da função w=f(u,v), dada implicitamente por u²+v²+w² = 1
Ou seja, o domínio de w=f(u,v) é dado por $$ D(f) = \{ (u,v) \in \mathbb{R} ^2 |\;\;\; u^2+v^2\leq 1 \},$$ enquanto a imagem desta função é dada por $$ Im(f) = \left\{ z \in \mathbb{R} |\;\;\; 0 \leq z \leq 1 \right\} .$$
EXEMPLO
Represente graficamente o domínio das funções:
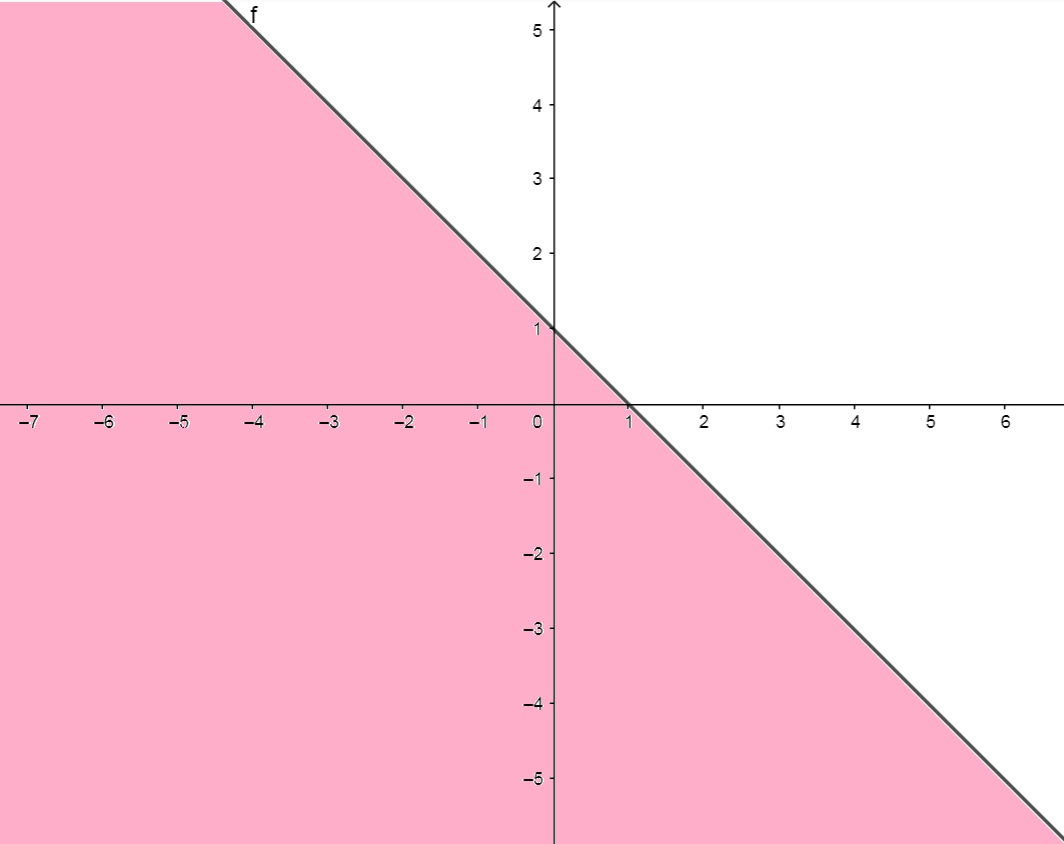
a) f(x,y) = \sqrt{1-x-y}
1-x-y \geq \Rightarrow x+y \leq 1 \Rightarrow y \leq 1-x
Desta forma, temos a região do plano abaixo da reta y=1-x dada por
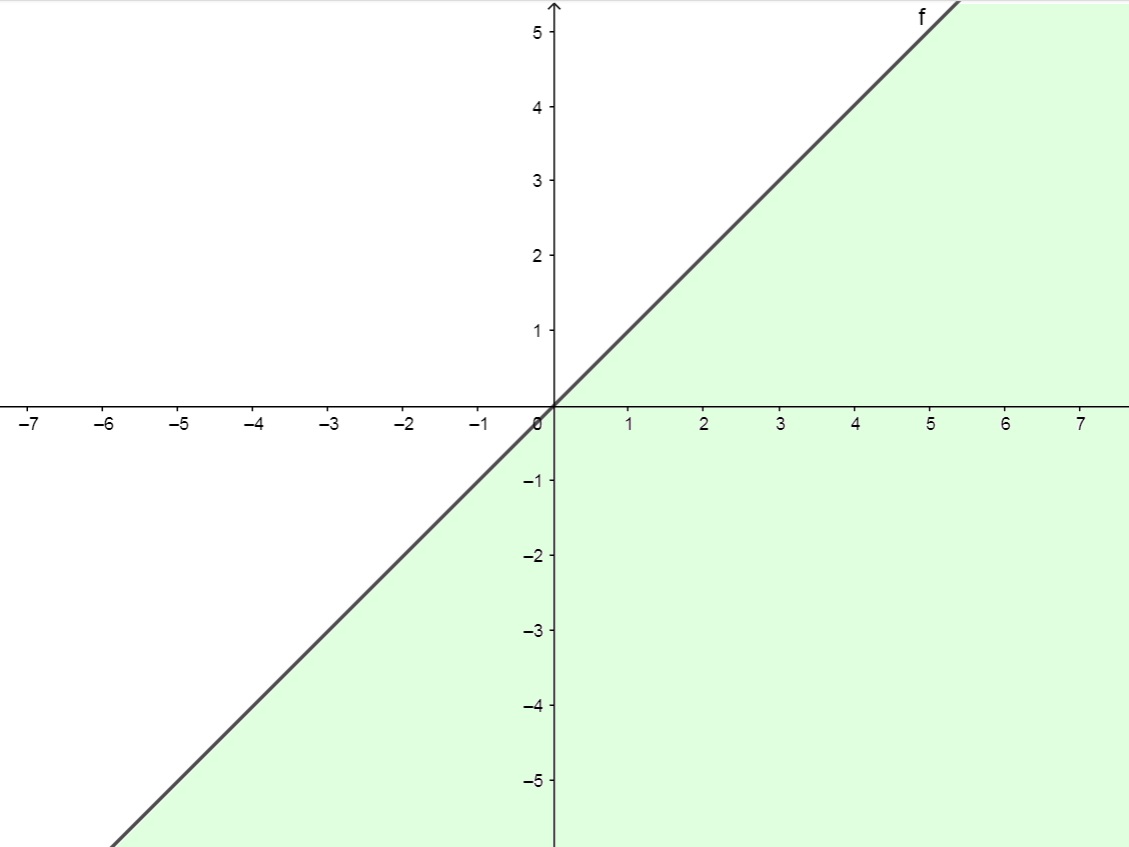
b) f(x,y) = \ln{(x-y)}
x-y>0 \Rightarrow x>y
Desta forma, temos a região do plano abaixo da reta y=x dada por
c) z=f(x,y) tal que 4x^2 + y^2 + z^2 = 1\;\;\;z \leq 0
Nesse caso, z=\sqrt{1-4x^2-y^2}.
Assim, 1-4x^2-y^2 \geq 0 \Rightarrow 4x^2-y^2 \leq 1
Desta forma, temos a região do plano exterior à hipérbole de eixo real sobre o eixo x e centrada na origem:
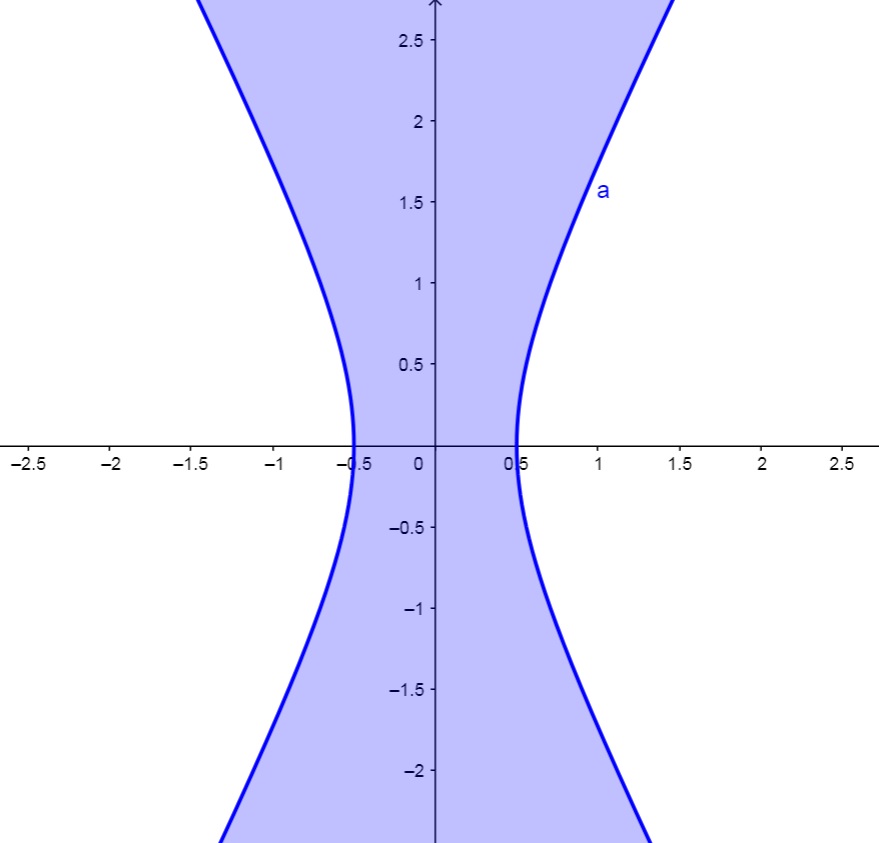
Gráfico de uma Função de Várias Variáveis
Seja z=f(x,y), com (x,y) \in A, uma função real de duas variáveis reais.
O conjunto $$G_f=\left\{ (x,y,z) \in \mathbb{R} ^3 / z=f(x,y),\;\;\; (x,y) \in A \right\}$$ denomina-se gráfico de f.
EXEMPLO
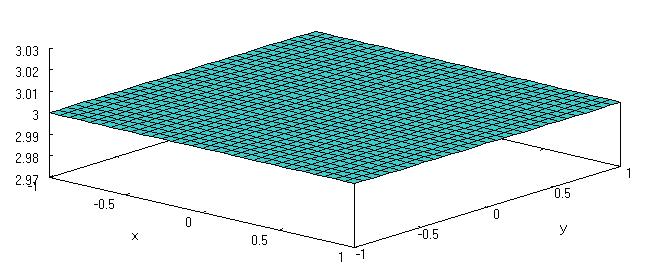
O gráfico da função constante f(x,y) = k é um plano paralelo ao plano xy.
EXEMPLO
Considere a função z=f(x,y) tal que x^2+y^2+z^2 = 4.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
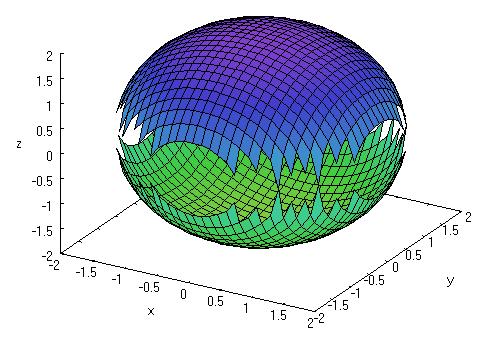
O gráfico desta equação é dada por $$G_f (z)= \left\{ (x,y,z) \in \mathbb{R} ^3 / z = \sqrt{4-x^2-y^2} \right\}.$$
Abaixo, cada superfície, respectivamente, representa uma das funções $$z_1 = \sqrt{4 – x^2-y^2 } \;\;\; (roxa)$$ e $$z_2 = – \sqrt{4 – x^2-y^2 } \;\;\; (verde)$$
EXEMPLO
Abaixo apresentamos os gráficos de algumas funções que julgamos interessantes:
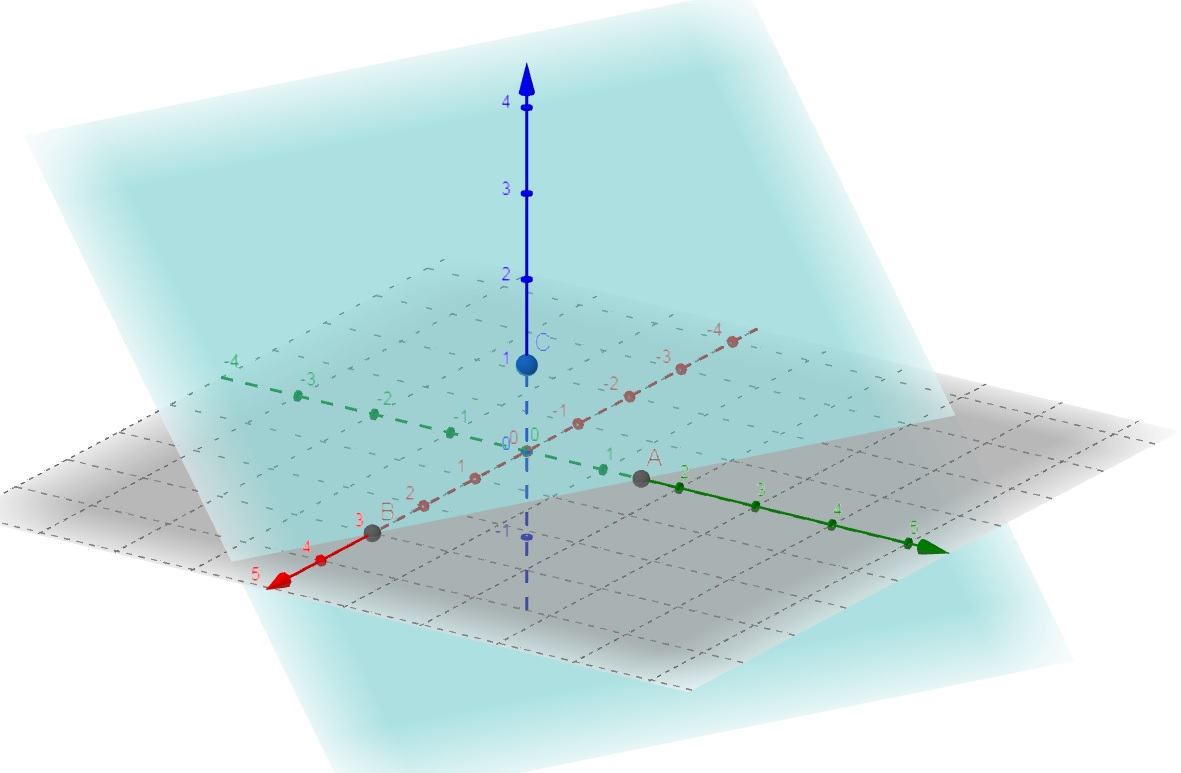
a) Observe que x+2y+3z = 3 é a equação de um plano inclinado que corta os eixos coordenados em x = 3 , y = 3/2 e z = 1. Esta equação pode ser escrita como uma função de duas variáveis z = f(x,y) , dada por $$f(x,y) = \frac{1}{3} (3-x-2y).$$
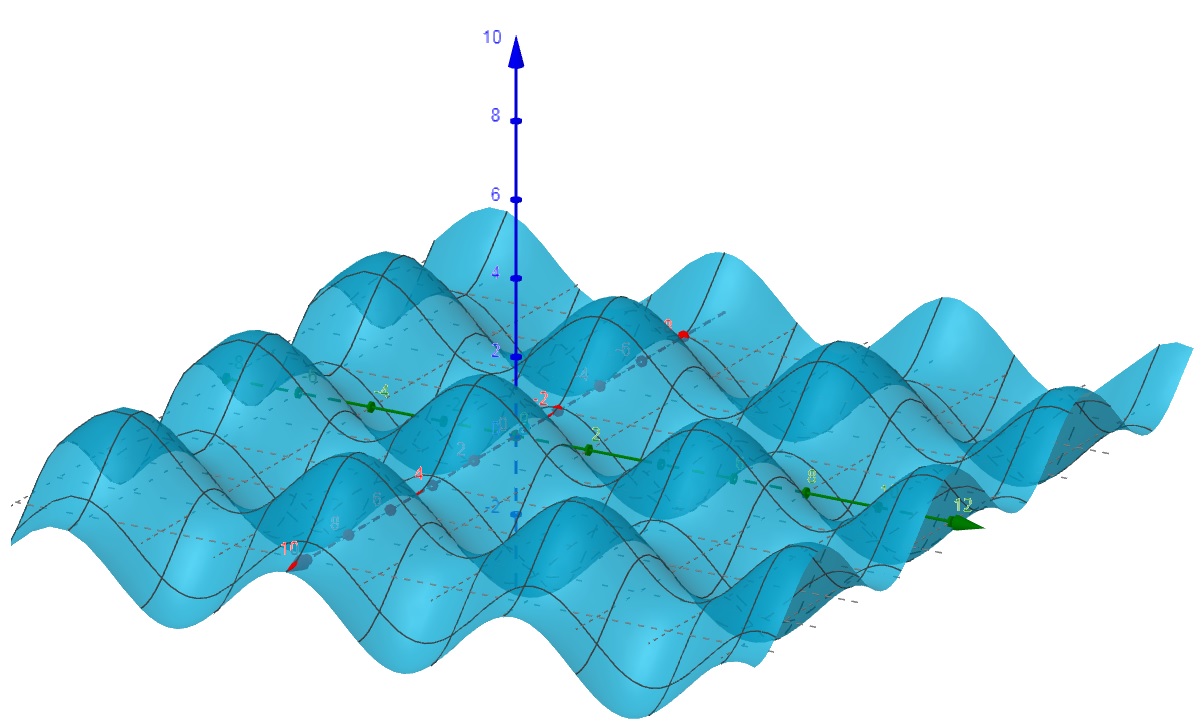
b) f(x,y) = sen(x) + cos(y)
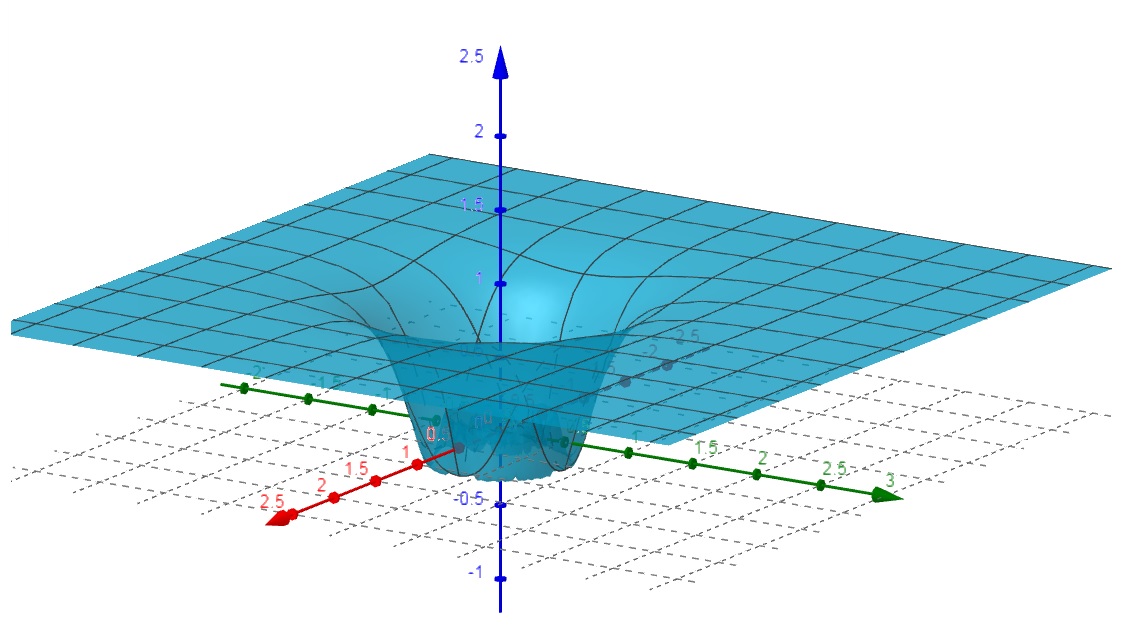
c) f(x,y) = (x^2 + y^2) sen \left( \dfrac{1}{x^2 + y^2} \right)
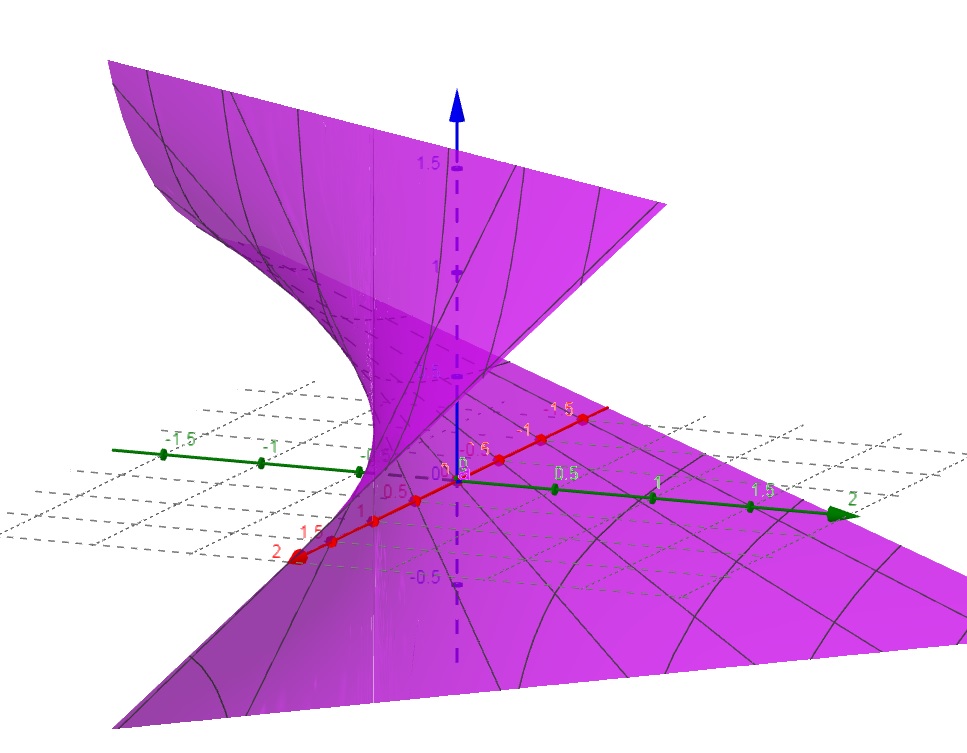
d) f(x,y) = \dfrac{y}{x-1}
e) f(x,y) = \dfrac{1}{x^2 + y^2}