PRECISANDO DE AJUDA COM SEUS EXERCÍCIOS SOBRE ESTE CONTEÚDO? Entre em contato com a gente via WhatsApp clicando aqui. |
Abaixo vamos apresentar uma lista de exercícios de funções com domínio no \mathbb{R} ^2 simplesmente pela facilidade em estabelecer gráficos e representações do domínio, e também por serem as funções que mais aparecem em aplicações de engenharia, por exemplo.
Uma função de duas variáveis reais a valores reais é uma função f: A \subset \mathbb{R} ^2\rightarrow \mathbb{R}. Uma função desta forma associa, a cada par (x,y) \in A, um único número f(x,y) \in \mathbb{R}. O conjunto A é chamado de domínio de f e será indicado por D_f. O conjunto $$Im_f = \left\{ f(x,y) \in \mathbb{R}/ (x,y) \in D_f \right \}$$ é a imagem de f. O conjunto $$G_f=\left\{ (x,y,z) \in \mathbb{R} ^3 / z=f(x,y),\;\;\; (x,y) \in A \right\}$$ denomina-se gráfico de f.
Domínio, Imagem e Gráfico de Campos Escalares | Lista de Exercícios
1. Determine os domínios de definição de cada uma das funções dadas abaixo e represente-os graficamente:
a) f(x,y) = \dfrac{xy}{\sqrt{x^2 - y^2}}
SOLUÇÃO: O domínio desta função é dado por $$ \{ (x,y) \in \mathbb{R} ^2 ; x^2 – y^2 \geq 0 \}$$ $$ \{ (x,y) \in \mathbb{R} ^2 ; x^2 \geq y^2 \}$$ $$ \{ (x,y) \in \mathbb{R} ^2 ; | x | \geq | y | \}$$
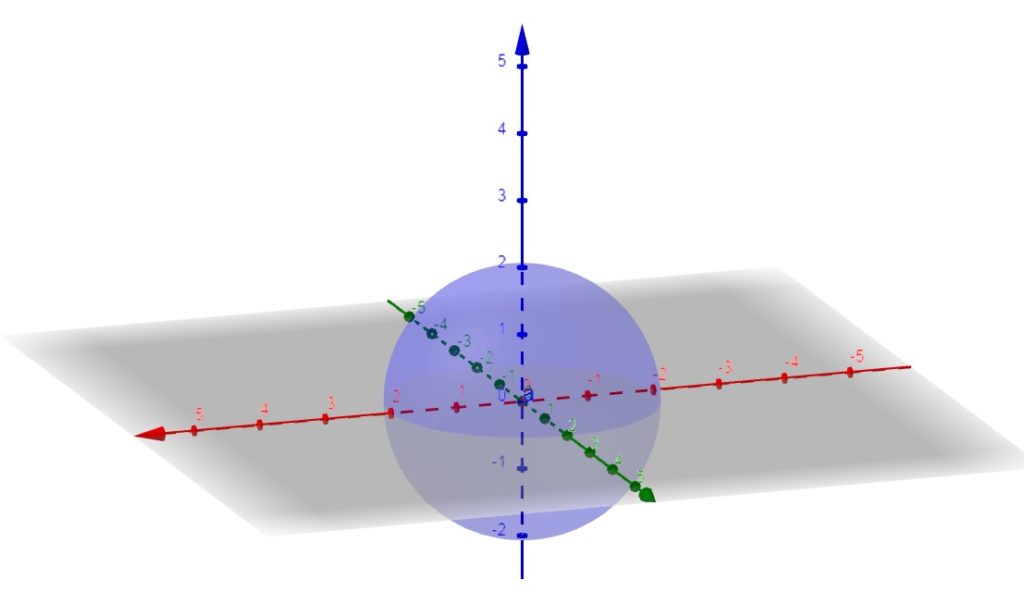
b) f(x,y,z) = \sqrt{16 - x^2 - y^2 - z^2}
SOLUÇÃO: O domínio desta função é dado por $$ \{ (x,y,z) \in \mathbb{R} ^3 ; 16 – x^2 – y^2 – z^2 \geq 0 \}$$ $$ \{ (x,y,z) \in \mathbb{R} ^3 ; x^2 + y^2 + z^2 \leq 16 \},$$ ou seja, o domínio desta função é uma esfera compacta de raio 4:
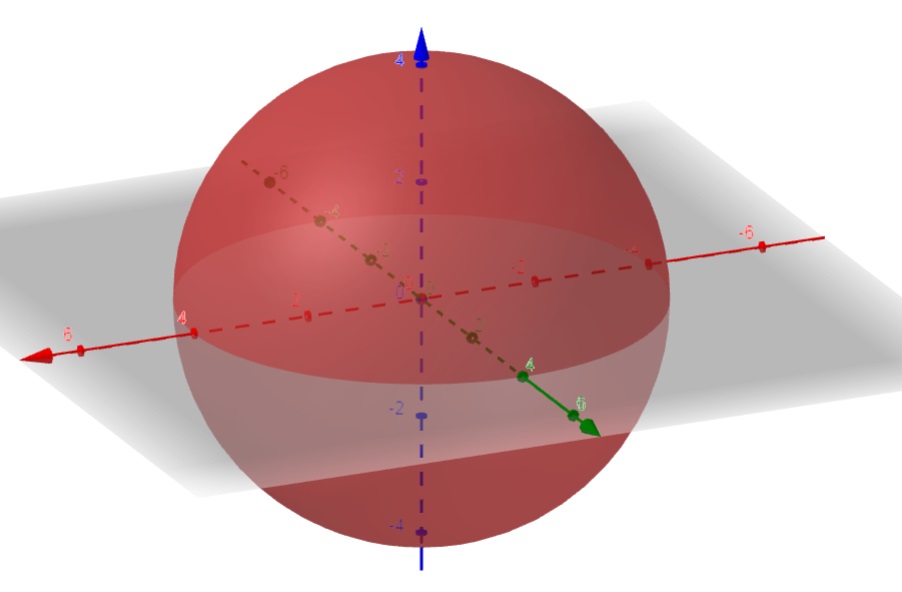
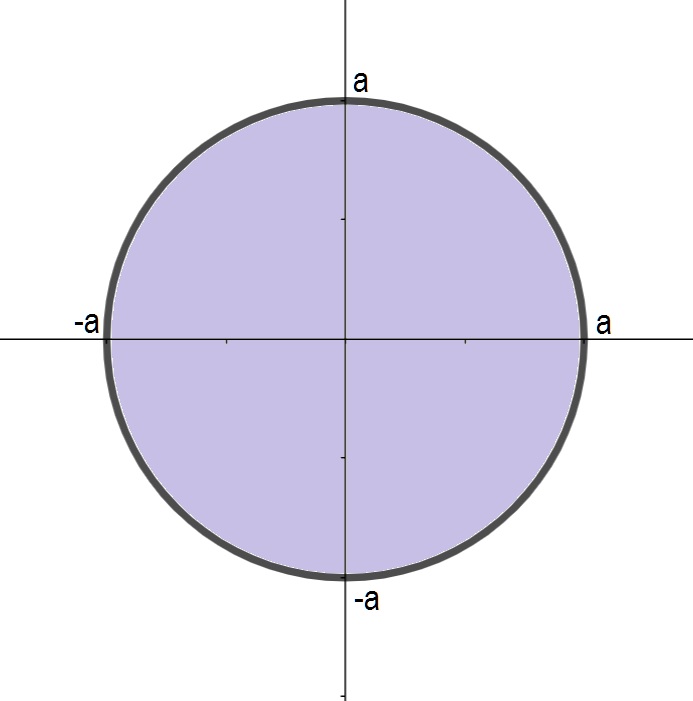
c) z = f(x,y), onde x^2 + y^2 + z^2 = a^2; \quad a >0 .
SOLUÇÃO: Neste caso, temos duas funções dadas implicitamente por z = \pm \sqrt{a^2 -x^2 - y^2} que possuem um mesmo domínio dado por $$ \{ (x,y) \in \mathbb{R} ^2 ; x^2 + y^2 \leq a^2 \}$$ que é um círculo de raio a>0.
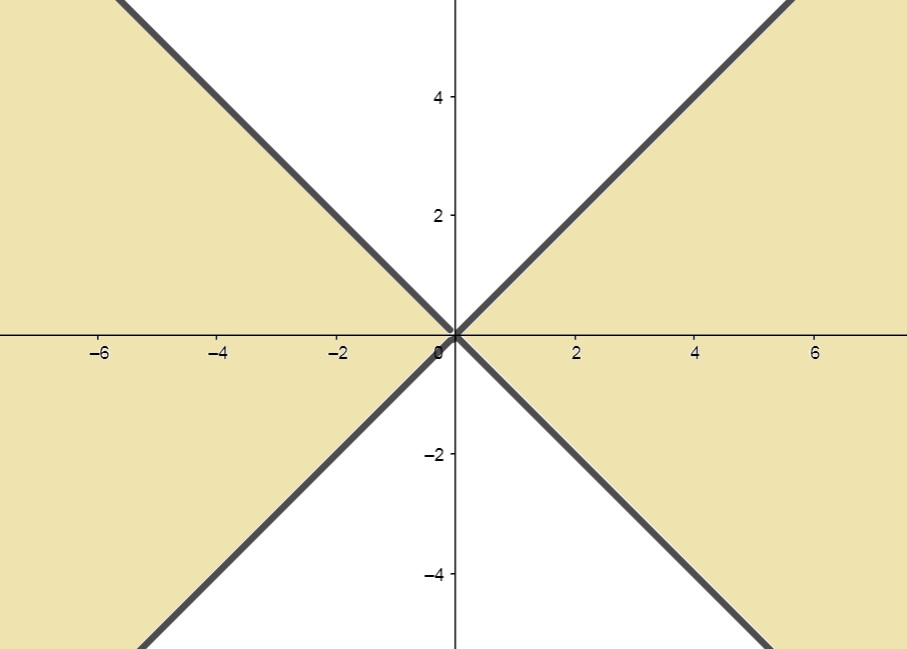
d) f(x,y) = \dfrac{x (y^2-1)}{x^2 - y^2};
SOLUÇÃO: Neste caso, observe que precisamos garantir que x^2 - y^2 \neq 0 , logo, obtemos y \neq \pm x . Graficamente, são todos os pontos do plano exceto os pontilhados abaixo:
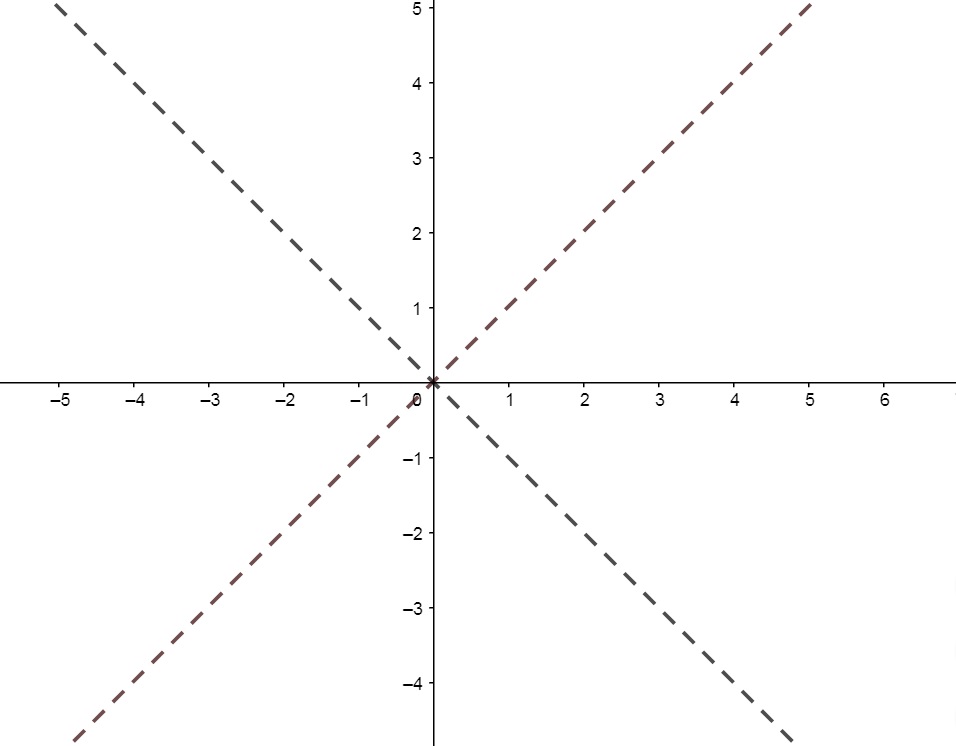
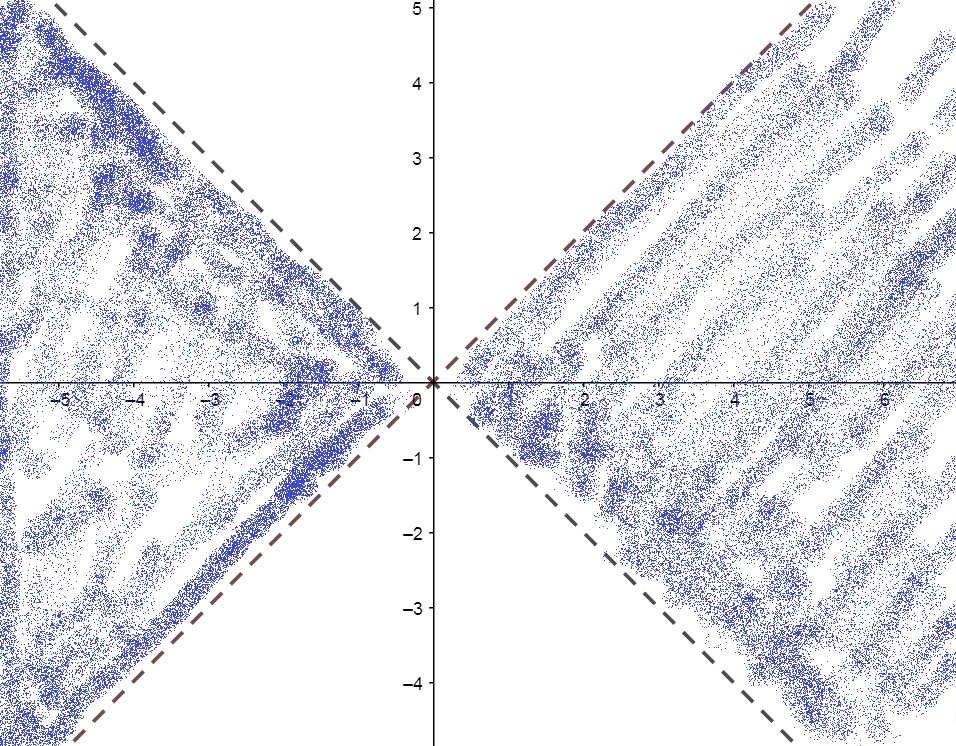
e) f(x,y) = \ln{(x^2 - y^2)};
SOLUÇÃO: Neste caso, observe que precisamos garantir que x^2 - y^2 > 0 , logo, obtemos y^2 < x^2 \Leftrightarrow y < |x| \Leftrightarrow -x < y < x . Graficamente, são todos os pontos do plano exceto os pontilhados abaixo:
f) f(x,y,z) = \sqrt{x^2+y^2+z^2 -4};
SOLUÇÃO: Neste caso, observe que precisamos garantir que x^2+y^2+z^2 -4 \geq 0 , logo, obtemos, graficamente, o espaço exterior à esfera com centro na origem e raio igual a 2:
2. Use softwares matemáticos para esboçar os gráficos das funções abaixo:
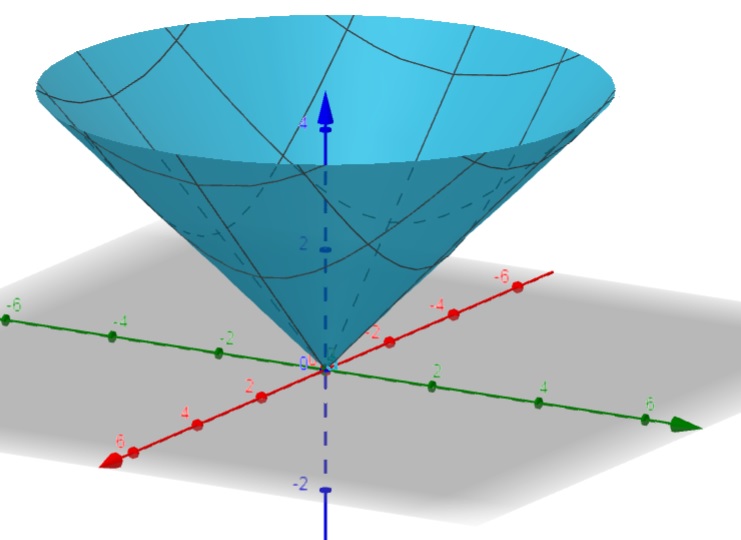
a) f(x,y) = \sqrt{x^2 + y^2}
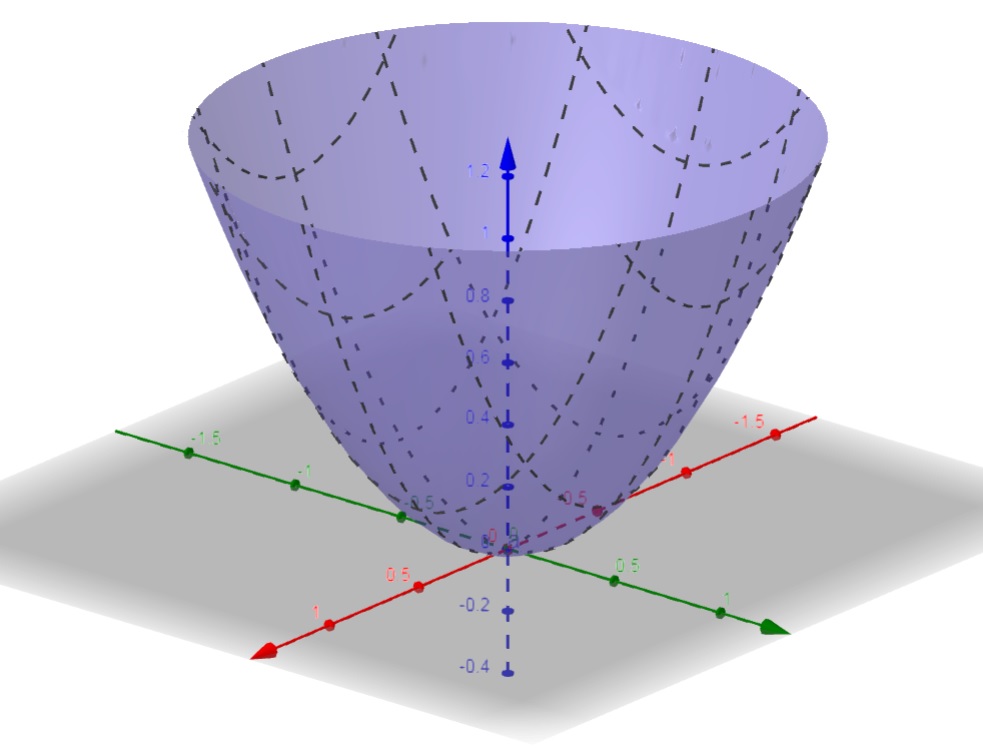
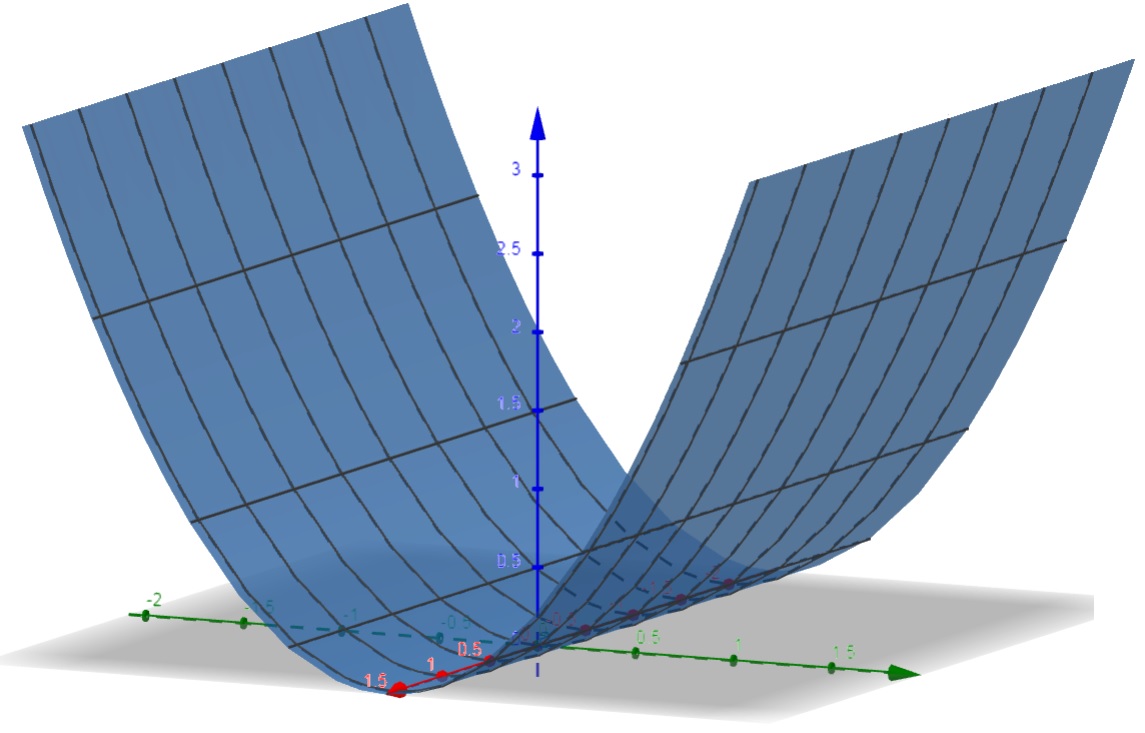
b) f(x,y) = x^2 + y^2
c) f(x,y) = - x^2 + y^2
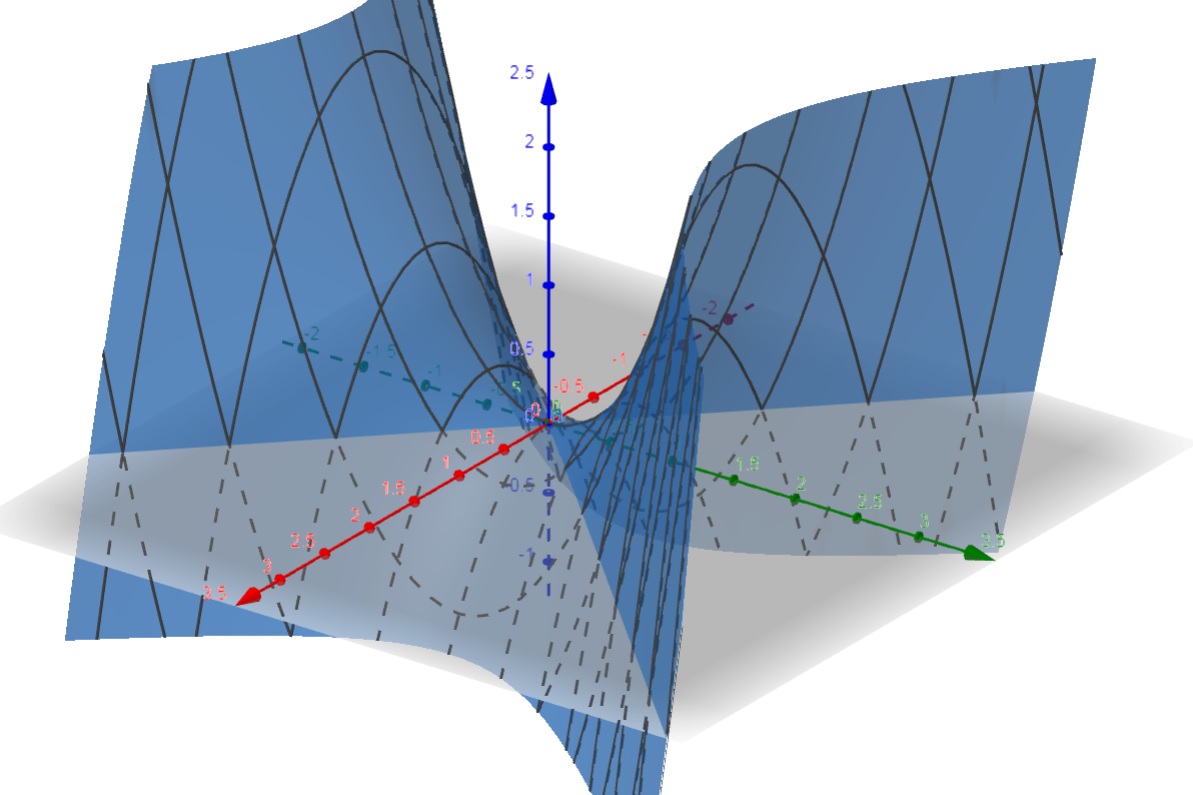
d) f(x,y) =- x^2 + y^2 (mesmo do anterior)
e) f(x,y) = y^2
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
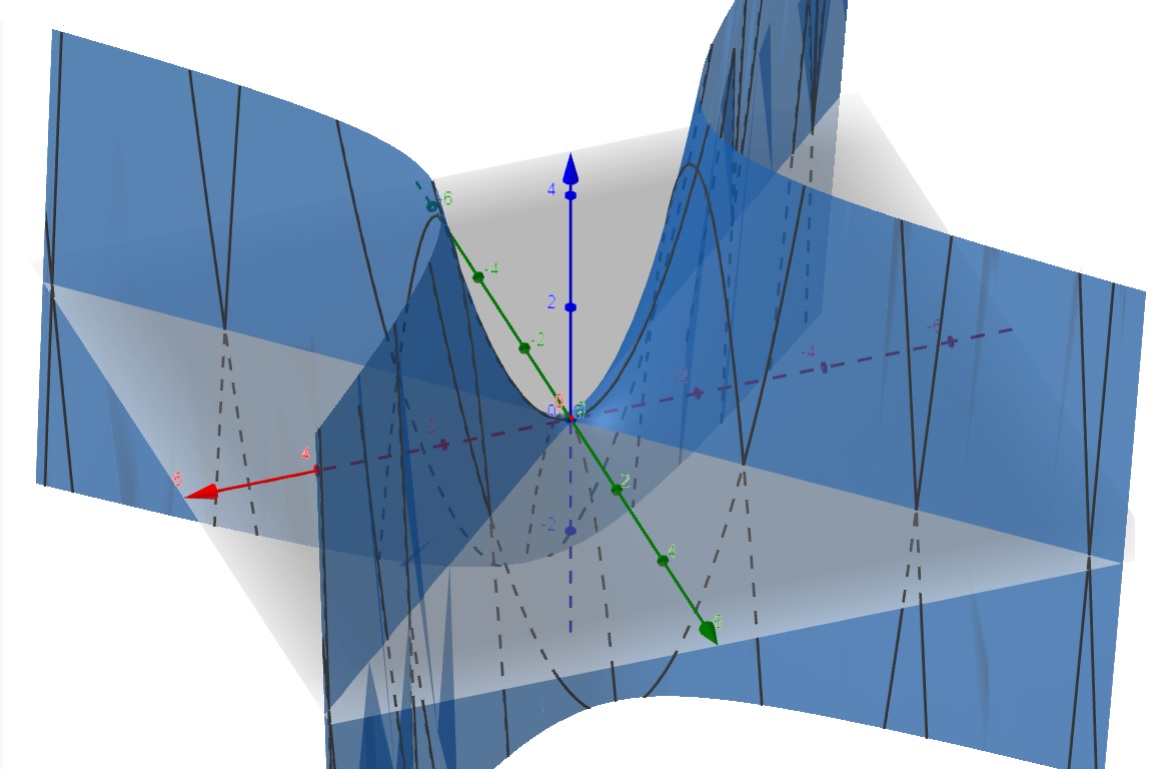
f) f(x,y) = x^2 - y^2
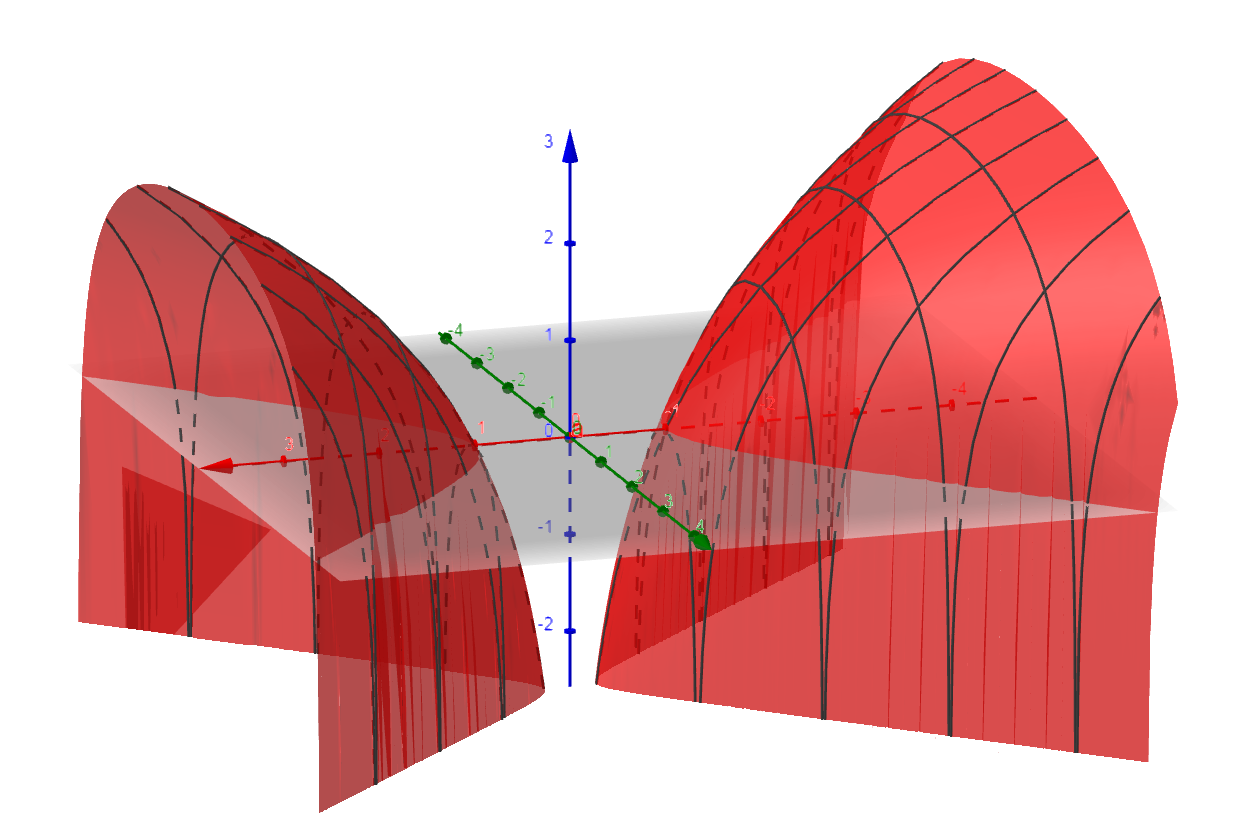
g) f(x,y) = \ln{ (x^2 - y^2)}
h) f(x,y) = sen^2 \sqrt{x^2 + y^2}
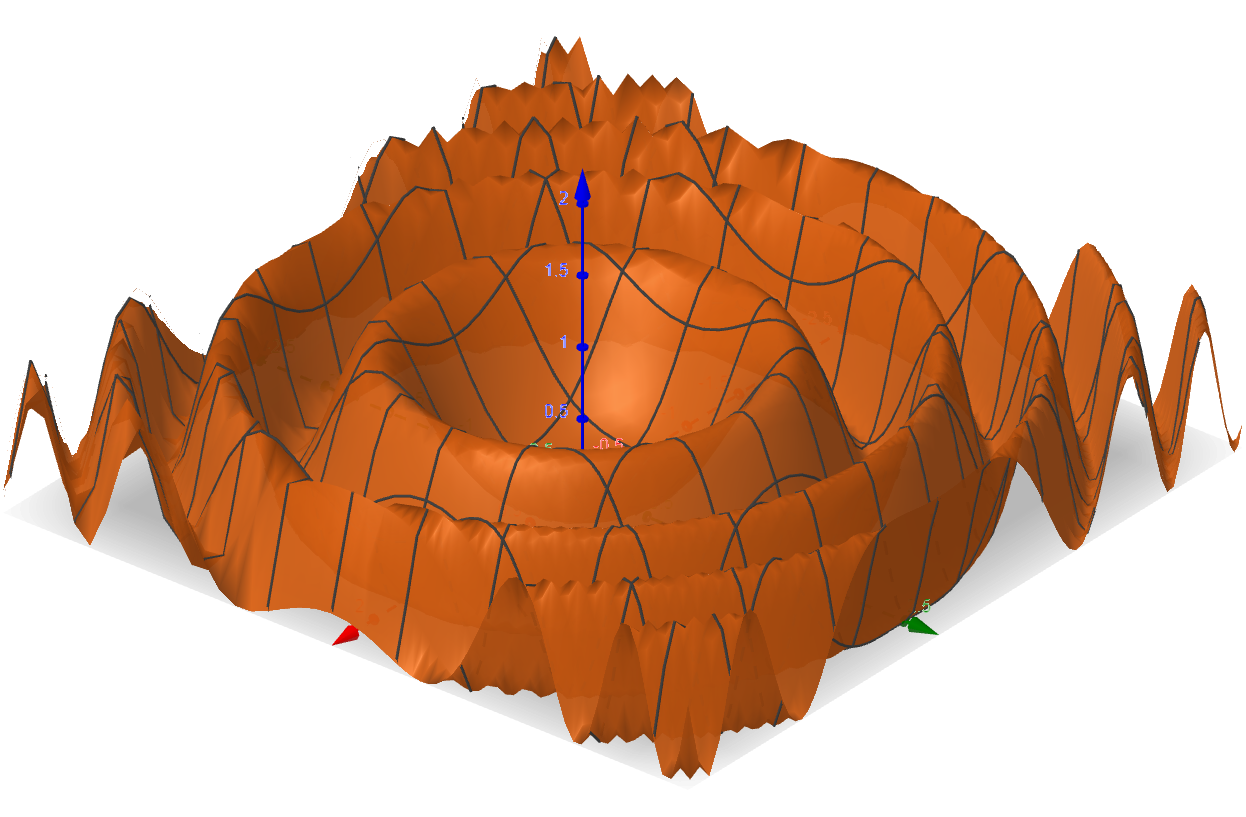
i) f(x,y) = \dfrac{sen(x^2 + y^2)}{x^2 + y^2}


Pingback: Funções de Várias Variáveis | Domínio, Imagem e Gráfico