A Função Erro de Gauss, denotadas por erf(x) e erfc(x) desempenha um papel relvante em muitas aplicações envolvendo Transformadas Integrais, como a Transformada de Fourier e a Transformada de Laplace. Essa função é definida por meio de uma integral.
A função \mathrm{erf}\left( x \right) foi objeto de estudo de matemáticos como De Moivre (1718-1733) e Laplace (1774), onde foi expressa através da integral $$\int{e^{-x^{2}}dx}.$$
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
A integral de probabilidade foi assim chamada porque é amplamente utilizada na teoria da probabilidade e estatística, aparecendo também em equações diferenciais. Posteriormente ela foi estendida para a Função Erro de Gauss, que foi desenvolvida para calcular a integral da distribuição normal, e em 1809, Gauss usou esta função para analisar dados astronômicos.
A Função Erro
DEFINIÇÃO (A Função Erro)
A função erro, denotada por erf(x) , é $$ erf(x) = \frac{2}{\sqrt{ \pi }} \int_{0}^{x}{e^{-u^2} du}.$$ A função erro complementar se define em termos da função erro: $$erfc(x) = 1 – erf(x).$$
No cálculo, mostra-se que $$ \int_{0}^{ \infty}{e^{-u^2} du} = \frac{\sqrt{ \pi }}{2} $$ ou $$ \frac{2}{\sqrt{ \pi }} \int_{0}^{ \infty}{e^{-u^2} du} = 1. $$ Logo, a função erro complementar pode ser escrita como $$ erfc(x) = \frac{2}{\sqrt{ \pi }} \left[ \int_{0}^{ \infty}{e^{-u^2} du} – \int_{0}^{ x}{e^{-u^2} du} \right] = \frac{2}{\sqrt{ \pi }} \int_{x}^{ \infty}{e^{-u^2} du} .$$
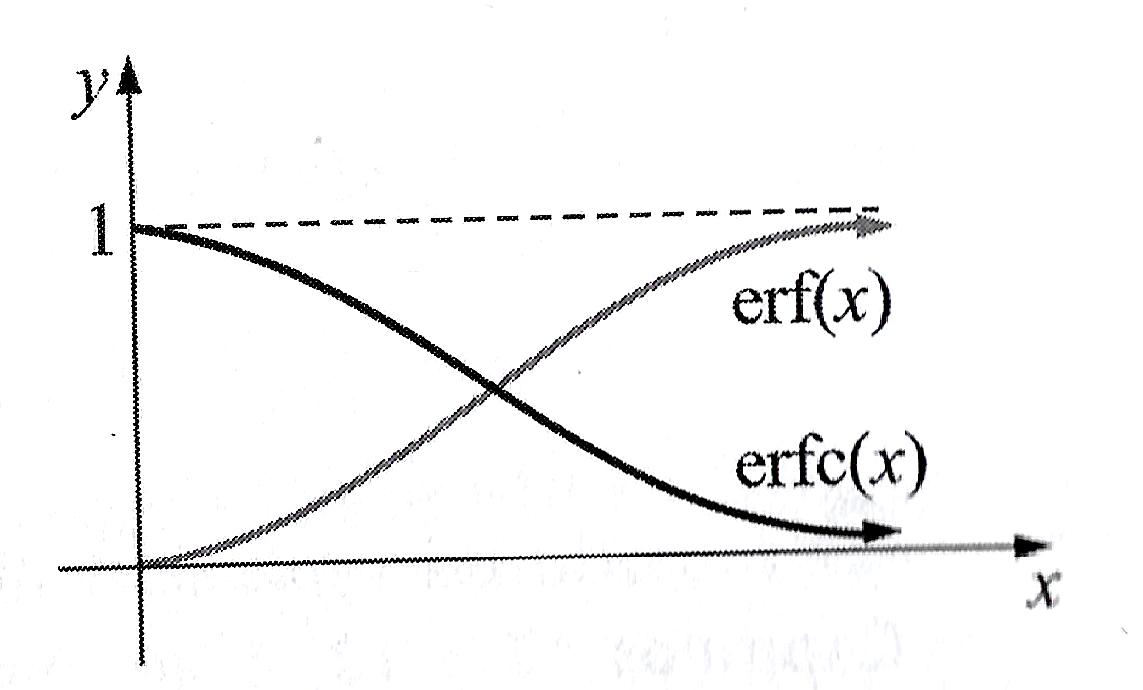
A figura acima exibe os gráficos das funções erro e erro complementar. Note que erf(0) = 0, erfc(0) = 1 e erf(x) \rightarrow 1 e erfc(x) \rightarrow \infty quando x \rightarrow \infty .
Além disso, podemos mostrar que $$1) \int \limits _{a}^{b}{e ^{-u^2}du} = \frac{\sqrt{ \pi} }{2} [ erf(b) – erf(a)] $$ $$2) \int \limits _{-a}^{a}{e ^{-u^2}du} = \frac{\sqrt{ \pi} }{2} erf(a) . $$
EXEMPLO: É possível mostrar que
1) efr( \sqrt{t} ) = \dfrac{1}{\sqrt{ \pi }} \int\limits^{t}_{0}{\dfrac{e^{- \tau }}{\sqrt{ \tau}}d \tau}
2) \int{ e^t \sqrt{t+1} dt} = \left( \dfrac{\sqrt{t}\,{e}^{t}}{2}+\dfrac{\sqrt{\pi }\,i\,\mathrm{erf}\left( i\,\sqrt{t}\right) }{4}\right)
3) \int{t^{-1/2} e^t dt} = - \sqrt{ \pi} i \text{erf} \left(i \sqrt{t} \right)
EXEMPLO: Calcule \int\limits_{e}^{e^4}{\frac{dx}{\sqrt{\ln{x}}}}.
Vamos usar a integração por substituição, fazendo $$ \ln{x} = u \qquad du = \frac{1}{x} dx \Leftrightarrow xdu = dx \Leftrightarrow e^u du = dx.$$ Assim, $$ \int{\frac{dx}{\sqrt{\ln{x}}}} = \int{ \frac{e^u }{ \sqrt{u} } du} = \\ = \int{u^{-1/2} e^u du} = \ \ – \sqrt{ \pi} \text{ierf} \left(i \sqrt{u} \right) = \ \ – \sqrt{ \pi} i \text{erf} \left(i \sqrt{\ln{x}} \right)$$
$$ \int\limits_{e}^{e^4}{\frac{dx}{\sqrt{\ln{x}}}} = – i \sqrt{ \pi} \text{erf} \left(i \right) + i \sqrt{ \pi} \text{erf} \left( 2i \right)$$
Transformadas de Laplace Envolvendo a Função Erro
O método da Transformada de Laplace é uma ferramenta muito poderosa na solução de EDO’s lineares e PVI’s correspondentes.
As principais transformadas de Laplace e suas inversas envolvendo a função erro estão tabeladas abaixo. Em sua maioria, estas transformadas são obtidas através de técnicas sofisticadas e não podem ser obtidas através das propriedades simples que já foram descritas neste artigo.
| TABELA DE TRANSFORMADA DE LAPLACE ENVOLVENDO A FUNÇÃO ERRO | |
| f(t), a> 0 | F(s)=\mathscr{L}\{f(t)\} |
| \dfrac{1}{\sqrt{\pi t^3}} e^{-a^2/4t} | \dfrac{e^{-a \sqrt{s}}}{\sqrt{s}} |
| \dfrac{a}{2\sqrt{\pi t^3}} e^{-a^2/4t} | e^{-a \sqrt{s}} |
| erfc \left( \dfrac{a}{2 \sqrt{t}} \right) | \dfrac{e^{-a \sqrt{s}}}{s} |
| 2 \sqrt{\dfrac{t}{\pi} }e^{-a^2/4t} - a erfc \left( \dfrac{a}{2 \sqrt{t}} \right) | \dfrac{e^{-a \sqrt{s}}}{s \sqrt{s}} |
| e^{ab} e^{b^2 t} a erfc \left( b \sqrt{t} + \dfrac{a}{2 \sqrt{t}} \right) | \dfrac{e^{-a \sqrt{s}}}{\sqrt{s} ( \sqrt{s} + b)} |
| e^{ab} e^{b^2 t} a erfc \left( b \sqrt{t} + \dfrac{a}{2 \sqrt{t}} \right) + erfc \left( \dfrac{a}{2 \sqrt{t}} \right) | \dfrac{ b e^{-a \sqrt{s}}}{\sqrt{s} ( \sqrt{s} + b)} |
| erf(\sqrt{t}) | \dfrac{1}{s \sqrt{s+1}} |
| erfc(\sqrt{t}) | \dfrac{1}{s} \left[ 1 - \dfrac{1}{\sqrt{s+1}} \right] |
| e^t erfc(\sqrt{t}) | \dfrac{1}{\sqrt{s} (s+1)} |
| e^t erf(\sqrt{t}) | \dfrac{1}{\sqrt{s} (s-1)} |
| e^{-Gt/C} erf \left( \dfrac{x}{2} \sqrt{\dfrac{RC}{t}} \right) | \dfrac{C}{Cs + G} \left( 1 - e^{-x \sqrt{RC s + RG}} \right) sendo C, G, R e x constantes |
| \sum \limits_{n=0}^{\infty}{\left[ erf\left( \dfrac{2n +1 +a}{2 \sqrt{t}} \right) - erf\left( \dfrac{2n +1 - a}{2 \sqrt{t}} \right) \right]} | \dfrac{\sinh a \sqrt{s} }{s \sinh \sqrt{s} } |
A Integral de Probabilidade
Existem extensas tabelas de valores de erf(x) e erfc(x) . Nas tabelas, a função erro costuma ser designada como Integral de Probabilidade.
Dentre as várias distribuições de probabilidade contínuas, esta função está ligada à distribuição normal, que apresenta grande aplicação em pesquisas científicas e tecnológicas. Grande parte das variáveis contínuas de interesse prático segue esta distribuição, aliada ao Teorema do Limite Central (TLC), que é a base das estimativas e dos testes de hipóteses, realizados sobre a média de uma população qualquer, e garante que a distribuição amostral das médias segue uma distribuição normal, independentemente da distribuição da variável em estudo.
A forma da distribuição normal de probabilidade é ilustrado pela curva em forma de sino apresentada na figura abaixo, onde \mu é a média:
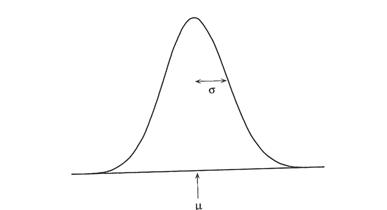
Muitas distribuições são em forma de sino e bastante simétricas com relação a média. Um modelo teórico frquentemente usado para este tipo de distribuição, é definido pela função de densidade $$ f(x) = \frac{1}{\sqrt{2 \pi} } e^{-x^2/2} . $$
É necessário que a probabilidade total seja igual a 1, isto é, $$ \int \limits _{- \infty}^{\infty}{f(x)} = \int \limits _{- \infty}^{\infty}{\frac{1}{\sqrt{2 \pi} } e^{-x^2/2} dx} = 1. $$ Além disso, a média, ou esperança, da distribuição é igual a 0 e o desvio-padrão é igual a 1.
Esta distribuição é chamada de normal ou gaussiana com média zero e desvio padrão um.
A função de distribuição normal é representada por $$ \Phi (x) = \int \limits _{- \infty}^{x}{\frac{1}{\sqrt{2 \pi} } e^{-t^2/2}dt}$$
Esta integral não pode ser expressa por um número finito de funções elementares.
O cálculo de probabilidades via distribuição normal envolve a solução de integrais que não são nada triviais.
Em virtude da grande aplicação da distribuição normal, procurou-se tabelar os valores de probabilidade, que seriam obtidos por meio da integração da função densidade de probabilidade normal num determinado intervalo.
A dificuldade para processar esse tabelamento se prendeu na infinidade de valores que \mu (média) e \sigma $ (desvio padrão) poderiam assumir. Nestas condições, teria que se dispor de uma tabela para cada uma das infinitas combinações de \mu e \sigma , ou seja, em cada situação que se quisesse calcular uma probabilidade.
Para resolver este problema, podemos obter uma nova forma para a distribuição normal, que não seja influenciada por \mu e \sigma . O problema foi solucionado mediante o emprego de uma nova variável, definida por $$z=\frac{x-\mu}{\sigma}.$$
A tabela de distribuição normal com média igual a $0$ e desvio padrão igual a $1$ é dada na figura abaixo. Veja que na tabela da distribuição normal, os valores apresentados na primeira coluna correspondem à parte inteira e decimal do valor de z , enquanto os valores da primeira linha correspondem à parte centesimal.
Já os valores encontrados no meio da tabela correspondem às probabilidades dos respectivos valores compreendidos entre zero e z .
Usando a função erro podemos tabelar valores para esta distribuição, dada pela tabela abaixo:
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Já que a distribuição normal vai de - \infty a \infty , ela não parece ser adequada para aplicações nas ciências naturais.
Nenhuma quantidade real pode alcançar um valor infinito. Entretanto deveríamos julgar a distribuição normal de um ponto de vista diferente.
Devido à ligação com a função exponencial, a função densidade de distribuição normal decai muito rápido quando z aumenta.
A probabilidade de um valor externo ao intervalo [-3,3] é de 0,0027, e de um valor externo ao intervalo [-4,4] é somente 0,00004. Tal evento é praticamente impossível.
Até por isso, nossa tabela infere valores para z até 3,99, calculado à partir de 0, tem valor de \Phi (z) igual a aproximadamente 0,5000 , que é corresponde a toda área de probabilidade definida pela integral.
A função densidade normal de probabilidade no caso geral é dada por $$ f(x) = \frac{1}{\sigma \sqrt{2 \pi} } e^{-(x- \mu )^2/2 \sigma ^2 }$$ onde \mu é a média e \sigma é o desvio padrão. Estes parâmetros determinam a posição e a forma da distribuição normal de probabilidade.
À semelhança de outras variáveis aleatórias contínuas, os cálculos de probabilidade com quaisquer distribuições normais são feitos calculando-se as áreas sob o gráfico da função densidade de probabilidade, que são dados por $$ f(x) = \frac{1}{\sigma \sqrt{2 \pi} } e^{-(x- \mu )^2/2 \sigma ^2 }$$
Por fim, é importante observar que a distribuição normal foi introduzida muito antes de que Gauss tenha trazido a distribuição ao uso geral em matemática aplicada.
Um dos primeiros a estudar a distribuição normal foi Abraham de Moivre, matemático inglês de origem francesa.
Leia Mais:
- Função de Heaviside ou Degrau Unitário
- Função Gama | Fatorial Generalizado e Gama Incompleta
- O Delta de Dirac | Da definição à solução de Equações Diferenciais
- Transformada de Laplace | Das Definições Básicas à Função Delta
- Problemas do Milênio | Os 7 Problemas de Matemática para o Século XXI
- Equações Diferenciais Ordinárias de 1ª Ordem: Ricatti e Bernoulli