Equações Diferenciais Ordinárias Lineares de Ordem Superior

Uma equação diferencial, grosso modo, é uma relação entre uma função e suas derivadas.

Uma definição rigorosa do que é uma equação diferencial é dada da seguinte forma:

DEFINIÇÃO: Uma equação que contém as derivadas ou diferenciais de uma ou mais variáveis dependentes, em relação a uma ou mais variáveis independentes, é chamada de de equação diferencial.

Neste artigo queremos estabelecer as bases conceituais para o estudo das equações diferenciais lineares de ordem maior ou igual a 2.

Desta forma, esse artigo é essencial para quem quiser, ou precisar, mergulhar nas técnicas de solução das equações diferenciais.

O que é EDO Linear de Ordem Superior?

Uma equação diferencial é dita linear se é da forma a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y=g(t).

Observe que as equações diferenciais lineares são caracterizadas por duas propriedades:

1. A variável dependente e todas as suas derivadas são do primeiro grau, ou seja, a potência de cada termo as envolvendo é igual a 1;
2. Cada coeficiente depende apenas apenas da variável independente.

Por outro lado, uma equação diferencial que não se encaixe neste formato é dita não-linear.

EXEMPLO: A equação diferencial y''' + 2e^t y''+ y' = t^4 é uma equação linear, porém a equação diferencial y''' + 2e^t y''+ yy' = t^4 é não-linear por causa do termo yy'.

Problema de Valor Inicial de Ordem Superior

Para uma equação diferencial de n-ésima ordem, o problema a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y=g(t) sujeito a $$ y(t_0) = y_0, y'(t_0) = y’_0, …, y^{(n-1)}(t_0) = y^{(n-1)}_0 . $$ em que y_0, y'_0, ..., y^{(n-1)}_0 são constantes arbitrárias, é chamado de um problema de valor inicial.

Os valores específicos y(t_0) = y_0, y'(t_0) = y'_0, ..., y^{(n-1)}(t_0) = y^{(n-1)}_0 são chamados de condições iniciais. As soluções serão procuradas em um intervalo I que contenha t_0 .

TEOREMA (Existência de uma Única Solução)

Sejam a_0 (t), a_1 (t),...,a_n (t) e g(t) continuas em um intervalo I com a_n (t) \neq 0 para todo t. Se t = t_0 é algum ponto deste intervalo, então existe uma única solução y(t) para o problema de valor inicial $$ a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +…+a_n (x) y=g(t)$$ $$ y(t_0) = y_0, y'(t_0) = y’_0, …, y^{(n-1)}(t_0) = y^{(n-1)}_0$$ neste intervalo.

EXEMPLO: Como os coeficientes da equação y'' - 4y = 12t sujeito a y(0) = 4 e y'(0) = 1 são contínuos em qualquer intervalo contendo t = 0 .

Sendo assim, a solução deste problema de valor inicial dada pela função y(t) = 3 e^{2t} + e^{-2t} - 3x é única.

EXEMPLO: O problema de valor inicial 3y''' + 5y'' - y' +7y = 0, y(1)=0, y'(1) = 0, y''(1) = 0, possui a solução trivial y (t) = 0 . Como a equação de terceira ordem é linear com coeficientes constantes, segue-se que todas as condições do Teorema de Existência e Unicidade são satisfeitas. Logo, y (t) = 0 é a única solução em qualquer intervalo contendo t = 1 .

Problema de Valor de Contorno

Um outro tipo de problema consiste em resolver uma equação diferencial de ordem dois ou maior na qual a variável dependente y ou suas derivadas são especificada em pontos diferentes.

Um problema como $$ a_2 (t) y” + a_1 (t) y’ +a_0 (t) y=g(t)$$ $$ y(a) = y_0, y(b) = y_1$$ é chamado de problema de valor de contorno. Os valores especificados como y(a) = y_0 e y(b) = y_1 são chamados de condições de contorno ou de fronteira.

Uma solução para o problema em questão é uma função que satisfaça a equação diferencial em algum intervalo I, contendo a e b, cujo gráfico passa pelos pontos (a, y_0) e (b, y_1) como mostra a figura abaixo

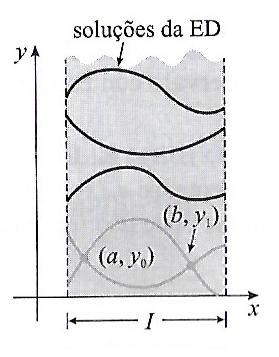
Para uma equação diferencial de segunda ordem, outras condições de contorno podem ser $$y’ (a) = y’_0, \;\;\; y(b) = y_1 ;$$ $$y (a) = y_0, \;\;\; y'(b) = y’_1 ;$$ ou $$y’ (a) = y’_0, \;\;\; y'(b) = y’_1 ,$$ em que y_0 , y'_0, y_1 e y'_1 denotam constantes arbitrárias.

Estes três pares de condições são casos especiais das condições gerais de contorno $$ \alpha _1 y(a) + \beta _1 y'(a) = \gamma _1$$ $$ \alpha _2 y(b) + \beta _2 y'(b) = \gamma _2 .$$

No próximo exemplo veremos que quando as condições do Teorema da Existência e Unicidade são satisfeitas, um problema de valor de contorno por ter

1. várias soluções;
2. uma única solução;
3. nenhuma solução.

EXEMPLO: Problemas de valor de contorno são frequentemente encontrados nas aplicações de equações de diferenciais parciais. Na solução da Equação da Onda, por exemplo, chegamos ao problema de valor de contorno $$ \ddot{F}(x) – k F(x) = 0; F(0)=F(L) = 0.$$

Usando os métodos adequados para EDOs lineares de 2ª ordem, encontramos a solução $$F(x) = A e^{-\sqrt{k}x}+Be^{\sqrt{k}x}.$$

Pelas condições iniciais $$F(0) = A + B = 0 \Leftrightarrow A=-B$$ e $$F(l) = A e^{-\sqrt{k}l}+Be^{\sqrt{k}l} = -B e^{-\sqrt{k}l}+Be^{\sqrt{k}l} = 0 \Leftrightarrow B = 0 \Rightarrow A=0,$$ ou seja, F(x) = 0 se k>0.

Desta forma, devemos ter que k<0. Sendo assim, tomando k = -p^2, obtemos $$F(x) = A \cos{px}+B\sin{px}.$$ Pela condições iniciais,

$$F(0) = A = 0$$ e $$F(L) = B\sin{pl} = 0 \Leftrightarrow pl = n\pi \Leftrightarrow p = \frac{n \pi}{l}.$$

Desta forma, podemos dizer existem infinitas funções dadas por $$F_n (x) = B \sin{\left( \frac{n \pi}{l} x \right)}$$ que satisfazem a equação acima.

Porém, cada solução possui coeficientes B que podem variar de solução para solução.

Portanto, é usual escrever $$F_n (x) = B_n \sin{\left( \frac{n \pi}{l} x \right)}.$$

Independência Linear de Funções

Um conjunto de funções é dito linearmente independente em um intervalo se as únicas constantes para as quais $$c_1 f_1(x) + c_2 f_2(x) + c_3 f_3(x) + … + c_n f_n(x) = 0,$$ para todo x no intervalo, são c_i = 0; i = 1, 2, ..., n.

Dizemos que um conjunto  f_1(x) , f_2(x) , f_3(x) , ... ,  f_n(x) é linearmente dependente em um intervalo se pelo menos uma função pode ser expressa como uma combinação linear das outras funções.

Observe que no caso de duas funções f_1 (x) e f_2 (x), elas são linearmente dependentes, então uma é simplesmente múltipla da outra, ou seja, se ambas são linearmente dependentes, então f_1 (x) = k f_2 (x).

Por outro lado, duas funções são linearmente independentes quando nenhuma delas é múltipla da outra em um dado intervalo.

EXEMPLO: 1) São funções linearmente dependentes no intervalo ( - \infty , \infty ), f_1(x) = sen(2x) e f_2(x) = sen(x)cos(x) . Para verifica isto, basta lembrar que sen(2x) = 2 sen(x) cos(x) .

2) As funções f_1 (x) = cos ^2 (x) , f_2 (x) = sen ^2 (x) , f_3 (x) = sec ^2 (x)   e f_4 (x) = tg ^2 (x) são linearmente dependentes no intervalo \left( -\dfrac{ \pi }{2} , \dfrac{ \pi }{2} \right)  , pois as relações cos ^2 (x) + sen ^2 (x) = 1 e sec^2 (x) - tg ^2 (x) = 1 nos garantem que c_1 = c_2 = c_4 = 1 e c_3 = -1 satisfazem a equação $$ c_1 cos^2 (x) + c_2 sen^2 (x) + c_3 sec^2 (x) + c_4 tg^2 (x) = 0.$$

O Determinante Wronskiano

Existe uma ferramenta usada para determinar a independência linear de n funções em um intervalo, desde que cada função seja diferenciável pelo menos n-1 vezes.

TEOREMA (Critério para Independência Linear de Funções)

Suponha que  f_1(x) , f_2(x) , f_3(x) , ... ,  f_n(x) sejam diferenciáveis pelo menos n-1 vezes. Se o determinante $$W \left( y_1 , y_2, … , y_n \right) = \left| \begin{array}{cccc} f_1 (x) & f_2 (x) & … & f_n (x) \\ f’_1 (x) & f’_2 (x) & … & f’_n (x) \\ \vdots & \vdots & & \vdots \\ \\ f^(n-1)_1 (x) & f^(n-1)_2 (x) & … & f^(n-1)_n (x) \end{array} \right| $$ for diferente de zero em pelo menos um ponto do intervalo I, então as funções  f_1(x) , f_2(x) , f_3(x) , ... ,  f_n(x) serão linearmente independentes no intervalo.

Este determinante, conhecido como Determinante Wronskiano, numa referência a Josef Maria Hoëne Wronski, matemático polonês conhecido pela excentricidade e por estabelecer esta condição suficiente para a independência linear de n funções em um intervalo.

EXEMPLO: Podemos perceber facilmente que y_1(t)=e^{-2t}\;\;\;e\;\;\;y_2(t)= e^{-3t} são linearmente independentes em todo a reta real, pois o wronskiano é dado por

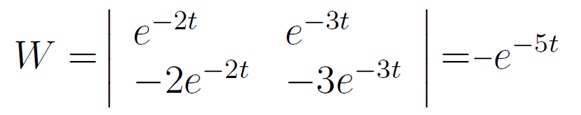
Equações Homogêneas de Ordem Superior

Uma equação diferencial de n-ésima ordem da forma a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y=0 é chamada de homogênea, enquanto a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y=g(t) com g(x) não identicamente nula, é chamada de não-homogênea.

A palavra homogênea neste contexto não se refere aos coeficientes como sendo funções homogêneas.

Além disso, toda EDO homogênea de ordem superior possui uma solução trivial, dada por y (t) = 0 .

EXEMPLO: A equação 2 y'' + 3 y' - 5y = 0 é de segunda ordem homogênea, enquanto x^3 y''' - 2x y'' + 5y' + 6y =  e^x é uma EDO de terceira ordem não-homogênea.

O Conjunto Fundamental de Soluções

Sejam  y_1(x) , y_2(x) , y_3(x) , ... ,  y_n(x)  n soluções para a equação diferencial linear homogênea de n-ésima ordem a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y=0 em um intervalo I. Então, o conjunto de soluções é linearmente independente em I se, e somente se, W \left( y_1 , y_2, ... , y_n \right) \neq 0 para todo x no intervalo.

DEFINIÇÃO (Conjunto Fundamental de Soluções)

Qualquer conjunto  y_1(x) , y_2(x) , y_3(x) , ... ,  y_n(x) de n soluções linearmente independentes para a equação diferencial linar homogênea de n-ésima ondem a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y=0  em um intervalo I é chamado de conjunto fundamental de soluções no intervalo.

É possível mostrar que sempre existe um conjunto fundamental de soluções para a equação diferencial linear homogênea de n-ésima ordem a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y=0 em um intervalo I.

O Princípio da Superposição.

O Princípio da Superposição garante que a soma de duas ou mais soluções para uma equação diferencial linear homogênea é também uma solução:

TEOREMA (Princípio da Superposição – Equações Homogêneas)

Sejam  y_1(x) , y_2(x) , y_3(x) , ... ,  y_k(x) soluções para a equação diferencial linear de n-ésima ordem homogênea a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y=0 em um intervalo I. Então, a combinação linear $$y = c_1 y_1(x) + c_2 y_2(x) + c_3 y_3(x) + … + c_k y_k(x) $$, em que c_i, i = 1,2,...,k são constantes arbitrárias, é também uma solução no intervalo.

Ou seja, este teorema mostra que qualquer solução para a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y=0 é obtida por uma combinação linear de funções em um conjunto fundamental de soluções.

TEOREMA (Solução Geral  – Equações Homogêneas)

Sejam  y_1(x) , y_2(x) , y_3(x) , ... ,  y_n(x) n soluções para a equação diferencial linear de n-ésima ordem homogênea a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y=0 em um intervalo I. A solução geral para a equação no intervalo é definida por $$y = c_1 y_1(x) + c_2 y_2(x) + c_3 y_3(x) + … + c_n y_n(x) $$ onde c_i, i = 1,2,...,n são constantes arbitrárias.

Em diversos momentos, a solução geral também é chamada de solução completa para a equação diferencial.

EXEMPLO: Como vimos anteriormente, y_1(t)=e^{-2t}\;\;\;e\;\;\;y_2(t)= e^{-3t} são linearmente independentes em todo a reta real, pois o wronskiano é dado por

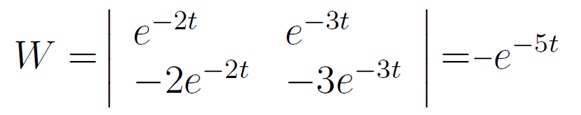
Ambas são soluções particulares da equação y''+5y'+6y = 0 . Sabemos, pela definição anterior que sua solução geral é dada por y(t) = c_1 e^{-2t} + c_2 e^{-3t}.

EXEMPLO: As funções y_1(x) = e^x , y_2(x) = e^{2x} e y_3(x) = e^{3x} satisfazem a equação de terceira ordem $$y”’ – 6y” + y’ – 6y = 0.$$ Como $$W \left( e^{x} , e^{2x}, e^{3x} \right) = \left| \begin{array}{ccc} e^{x} & e^{2x} & e^{3x} \\ e^{x} & 2e^{2x} & 3e^{3x} \\ e^{x} & 4e^{2x} & 9e^{3x} \end{array} \right| = 2 e^{6x} \neq 0 $$ para todo valor real de x , então \{e^x, e^{2x}, e^{3x} \} é um conjunto fundamental de soluções da equação y''' - 6y'' + y' - 6y = 0 . Portanto, $$y(x) = c_1 e^x + c_2 e^{2x} + c_3 e^{3x}$$ é a solução geral para a equação diferencial no intervalo.

EDO’s Lineares Não-Homogêneas de Ordem Superior

A solução geral para uma equação diferencial linear não-homogênea $$a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +…+a_n (x) y= g(x)$$ tem a estrutura

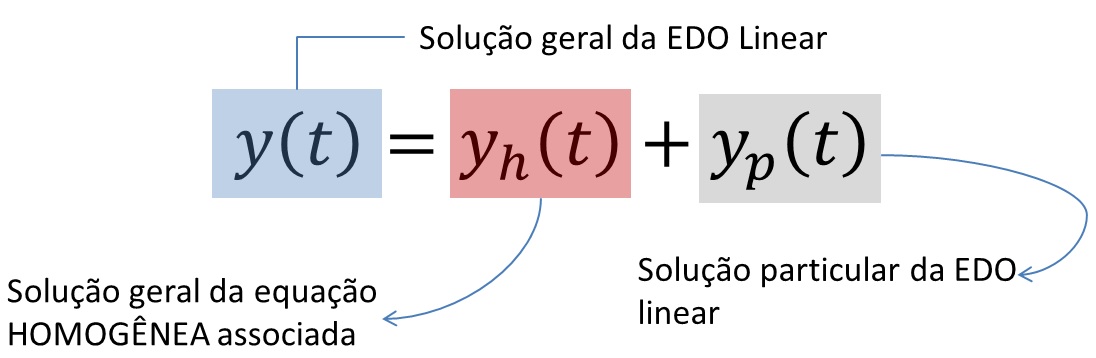
DEFINIÇÃO (Solução Geral – Equações Não-Homogêneas)

Sejam  y_1(x) , y_2(x) , y_3(x) , ... ,  y_n(x) n soluções para a equação diferencial linear de n-ésima ordem homogênea a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y=0 em um intervalo I e seja y_p qualquer solução para a equação não-homogênea a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y= g(x) no mesmo intervalo. Então $$y = c_1 y_1(x) + c_2 y_2(x) + c_3 y_3(x) + … + c_n y_n(x) + y_p (x)$$ é a solução geral da equação não-homogênea no intervalo, sendo c_i, i = 1,2,...,n são constantes arbitrárias.

EXEMPLO: Considere a a equação $$t^2 y” – 2y=3t^2 -1,\;\;\;t>0.$$

Facilmente podemos verificar que y_1(t) = t^2 e y_2(t) = t^{-1} são soluções da equação homogênea associada que forma um conjunto fundamental de soluções.

Assim, uma solução particular de $$t^2 y” – 2y=3t^2 -1,\;\;\;t>0,$$ pode ser encontrada pelo Método da Variação dos Parâmetros: \psi(t) = \dfrac{t^2}{3}\left( \dfrac{3t^2}{2} - \ln{t} \right) - \dfrac{t^{-1}}{3} \left( \dfrac{3t^5}{5} - \dfrac{t^3}{3} \right).

Portanto, a solução geral desta equação é dada por $$ y(x) = c_1 t^2 + c_2 \frac{1}{t} + \frac{t^2}{3}\left( \frac{3t^2}{2} – \ln{t} \right) – \frac{t^{-1}}{3} \left( \frac{3t^5}{5} – \frac{t^3}{3} \right).$$

TEOREMA (Princípio da Superposição – Equações Não-Homogêneas)

Sejam  y_{p1}(x) , y_{p2}(x) , y_{p3}(x) , ... ,  y_{pk}(x) soluções para a equação diferencial linear de n-ésima ordem homogênea a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y=g_i(x) em um intervalo I, correspondendo, respectivamente, a k funções distintas g_1 , g_2 , ... , g_k . Então, a combinação linear $$y_p = c_1 y_{p1}(x) + c_2 y_{p2}(x) + c_3 y_{p3}(x) + … + c_k  y_{pk}$$, em que c_i, i = 1,2,...,k são constantes arbitrárias, é uma solução particular para a_0 (x) y^{(n)} + a_1 (x) y^{(n-1)} +...+a_n (x) y= g_1(x) + g_2(x) + g_3(x) + ... + g_k(x) .

EXEMPLO: Considere y'' + y = 3\sin{2t} + t \cos{2t}.

Como y_1(t) = cos(t) e y_2(t) = sen(t) e W \left( y_1 , y_2 \right) = 1 , sabemos que a solução da equação homogênea associada y'' + y = 0 é dada por $$y_{H} (t) = c_1 cos(t) + c_2 sen(t).$$

Agora, basta encontrar y_p (t) = y_{p1}(t) + y_{p2}(t), onde y_{p1}(t) e y_{p2}(t) são, respectivamente, soluções de y'' + y = 3\sin{2t} e y'' + y = t \cos{2t}.

Neste caso, $$ y_{p}(t) = \frac{-17\,\mathrm{sin}\left( 4\,t\right) +\left( -3\,t-18\right) \,\mathrm{cos}\left( 4\,t\right) +175\,\mathrm{sin}\left( 2\,t\right) +\left( -57\,t-18\right) \,\mathrm{cos}\left( 2\,t\right) }{72} +$$ $$+ \frac{108\,\mathrm{sin}\left( t\right) +144\,\mathrm{sen}\left( t\right) \,\mathrm{cos}\left( t\right) +36\,t}{72}$$

Leia Mais:

• Método da Variação dos Parâmetros: EDOs de 2ª Ordem Lineares
• Equações Diferenciais Ordinárias Lineares de 1ª Ordem.
• Equações Homogêneas | EDOs de Primeira Ordem
• Solucionando EDO’s por Transformada de Laplace | Exercícios Resolvidos
• Equações Diferencias Ordinárias de 2ª Ordem: Equações Homogêneas
• Equações Diferenciais Ordinárias de 2ª Ordem, Homogêneas, com Coeficientes Constantes