Existem algumas funções que são de considerável interesse nas mais diversas áreas da ciência. Algumas delas, principalmente, são importantes nas soluções de equações diferenciais atreladas a modelagens de fenômenos descontínuos, como a FUNÇÃO DEGRAU UNITÁRIO ou FUNÇÃO DE HEAVISIDE.
A função de Heaviside ou função degrau unitário, desenvolvida pelo matemático e engenheiro eletricista Oliver Heaviside é simples de ser definida, pois é nula para argumento negativo e vale 1 para argumento positivo.
Esta função é frequentemente encontrada em engenharia, nos problemas que podem apresentar dualidade como “ligado” ou “desligado”.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
| Mais abaixo, neste artigo, temos uma vídeo-aula e uma lista com vários exercícios resolvidos sobre a Função de Heaviside. |
Quem foi Oliver Heaviside?
Oliver Heaviside, (nascido em 18 de maio de 1850, Londres – morreu em 3 de fevereiro de 1925, Torquay, Devon, Eng.) foi um físico que previu a existência da ionosfera, uma camada eletricamente condutora na atmosfera superior que reflete as ondas de rádio.
Em 1870, tornou-se telégrafo, mas a surdez crescente obrigou-o a se aposentar em 1874. Ele então se dedicou a investigações sobre eletricidade.
Em “Electrical Papers” (1892), ele tratou de aspectos teóricos de problemas em telegrafia e transmissão elétrica, fazendo uso de um método incomum de cálculo denominado cálculo operacional, hoje mais conhecido como método das transformadas de Laplace, para estudar correntes transitórias em redes.
Seu trabalho na teoria do telefone tornou prático o serviço de longa distância.
Na “Electromagnetic Theory” (1893-1912), ele postulou que uma carga elétrica aumentaria em massa à medida que sua velocidade aumentasse, uma antecipação de um aspecto da teoria da relatividade especial de Einstein.
Quando a telegrafia sem fio se mostrou eficaz em longas distâncias, Heaviside teorizou que existia uma camada condutora da atmosfera que permite que as ondas de rádio sigam a curvatura da Terra em vez de viajar para o espaço em linha reta.
Sua previsão foi feita em 1902, pouco depois de Arthur E. Kennelly, trabalhando nos Estados Unidos, fazer uma previsão semelhante.
Assim, a ionosfera foi conhecida como camada Kennelly-Heaviside por muitos anos.
A função degrau unitário.
Esta função degrau unitário é denotada por u(t-a) e dada por:
$$u(t-a) = \left\{ \begin{array}{lll}
0 & ; & t<a\\
1& ; & t \geq a\\
\end{array} \right. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;a \geq 0.$$
Observe que definimos a função degrau unitário somente para valores maiores do que zero de t, pois isso é suficiente para o estudo da Transformada de Laplace, mas num sentido mais amplo $$u(t-a) <0, \forall t<a.$$
O gráfico da função degrau é dado por:
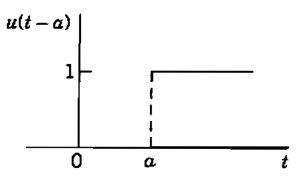 Gráfico da Função Degrau Unitário ou de Heaviside
Gráfico da Função Degrau Unitário ou de Heaviside
Se a = 0 esse gráfico é:
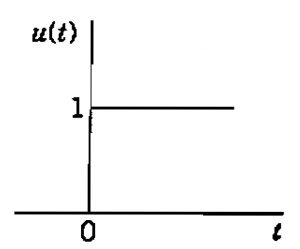 Função Degrau Unitário ou de Heaviside com a=0
Função Degrau Unitário ou de Heaviside com a=0
A Função Rampa
Observe que a representação gráfica em t=a não está com o rigor matemático para funções, pois deveria estar esboçado bolinhas abertas indicando que em t=a a função não está definida.
Esse tipo de representação gráfico é usado no contexto de transformada de Laplace.
Quando realmente for necessário definir um transição em t=0, toma-se uma aproximação linear e contínua para a função de Heaviside, chamada de função rampa:
$$g_\epsilon(t)=\left\{\begin{array}{ll}0,& t<-\epsilon\\ \frac{1}{2\epsilon}t+\frac{1}{2},&-\epsilon\leq t \leq \epsilon\\1,&t>\epsilon, \end{array}\right.
$$
para \epsilon<<1.
A função de Heaviside é o limite de g_\epsilon(t) se t\neq 0:
$$ \lim_{\epsilon\to 0}g_\epsilon(t) =u(t),\qquad t\neq 0.
$$
 Função Rampa
Função Rampa
A Função Degrau Inversa
Vamos esboçar o gráfico de h(t), onde h(t) = 1-u(t - a)
Temos que $$1-u(t-a) = \left\{ \begin{array}{lll}
1-0 & ; & t<a\\
1- 1& ; & t \geq a\\
\end{array} \right. = \left\{ \begin{array}{lll}
1 & ; & t<a\\
0 & ; & t \geq a\\
\end{array} \right.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;a \geq 0.$$
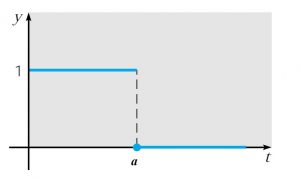
Função Pulso
Agora, vamos trabalhar com a seguinte situação: $$h(t) = u(t – a) – u(t-b)\;\;\;\;\;\;\;\;\; t\geq 0.$$
Temos que $$u(t-a) = \left\{ \begin{array}{lll}
0 & ; & t<a\\
1& ; & t \geq a\\
\end{array} \right.$$ e $$u(t-b) = \left\{ \begin{array}{lll}
0 & ; & t<b\\
1& ; & t \geq b\\
\end{array} \right.$$
Daí,
$$u(t-a) – u(t-b) = \left\{ \begin{array}{lll}
0-0 & ; & t<a\\
1-0 & ; & a \leq t < b\\
1-1 & ; & t \geq b
\end{array} \right. = \left\{ \begin{array}{lll}
0 & ; & t<a\\
1 & ; & a \leq t < b\\
0 & ; & t \geq b
\end{array} \right. $$
Essa é a função pulso, muito importante em aplicações. Abaixo você encontra o gráfico para $$h(t) = u(t – \pi) – u(t-2 \pi)\;\;\;\;\;\;\;\;\; t\geq 0.$$
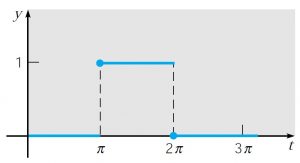
Analogamente, uma função do tipo $$ f(t)= \left\{ \begin{array}{lll}
0 & ; & t<a\\
g(t) & ; & a \leq t < b\\
0 & ; & t \geq b
\end{array} \right. $$ pode ser escrita como $$f(t) = g(t) [u(t-a) – u(t-b)].$$
Já uma função do tipo $$ f(t)= \left\{ \begin{array}{lll}
g(t) & ; & 0 \leq t<a\\
h(t) & ; & a \leq t
\end{array} \right. $$ pode ser escrita como $$f(t) = g(t) – g(t)u(t-a) + h(t)u(t-a)].$$
EXEMPLO:
A voltagem de um circuito é dada por $$E(t)= \left\{ \begin{array}{lll}
20t & ; &0 \leq t<5\\
0 & ; & t \geq 5\\
\end{array} \right. $$
Usando a forma dada acima, podemos considerar g(t) = 20t e h(t) =0 o que nos leva a $$ E(t) = 20t – 20t u(t-5).$$
Perceba que você chegaria neste mesmo resultado usado a Função Degrau Inversa, pois
$$E(t)= \left\{ \begin{array}{lll}
20t & ; &0 \leq t<5\\
0 & ; & t \geq 5\\
\end{array} \right. = 20t \left\{ \begin{array}{lll}
1 & ; &0 \leq t<5\\
0 & ; & t \geq 5\\
\end{array} \right. = 20t \left( 1 – u(t-5) \right) = 20t – 20t u(t-5).$$
A TRANSLAÇÃO
Quando multiplicada por outra função definida para t>0, a função degrau “cancela” uma porção do gráfico da função.
Por exemplo, o gráfico da função f(t) = sen(t) u(t - 2 \pi) é dado pela curva verde abaixo. Perceba que todo o gráfico de sen(t) foi “cancelado” para todos os valores de t < 2 \pi .

Se a>0, então o gráfico de y = f(t-a) é o gráfico de y = f(t), t \geq 0 , transladado para a direita em a unidades. Porém, quando f(t-a) é multiplicada por uma função degrau unitário u(t-a) como feito anteriormente então o gráfico da função y = u(t-a) f(t-a) coincide com o gráfico de y = f(t-a) para t \geq 0 , mas é identicamente nulo para os demais valores de t maiores do que zero, como mostrado na figura abaixo.
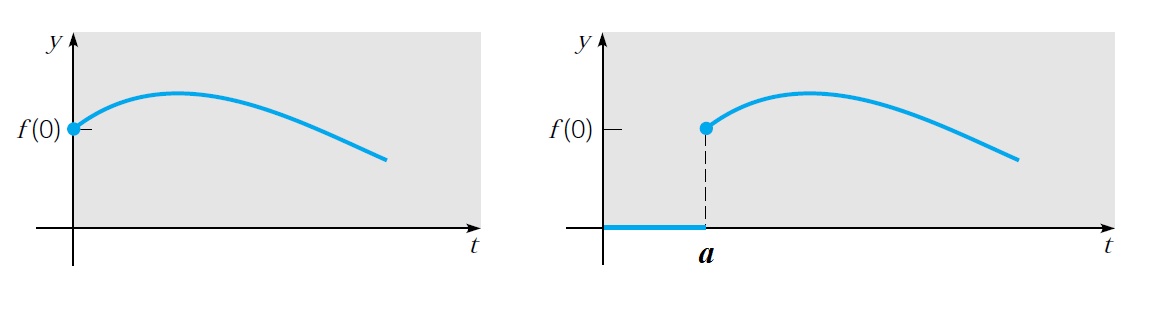 Translação de f(t)
Translação de f(t)
Observe que assim feito, a função não será truncada, mas transladada.
Para uma função f definida para t\geq 0, considere a função g dada por $$g(t) = \left\{ \begin{array}{lll}
0 & ; & t<a\\
f(t-a)& ; & t\geq a\\
\end{array} \right.$$ que representa a translação de f a uma distância a$.
Nos termos da função degrau unitário podemos escrever g(t) como $$g(t) = u(t-a)f(t-a).$$
A TRANSFORMADA DE LAPLACE DA FUNÇÃO DEGRAU
A transformada de u(t-a) é dada por $$\mathscr{L}\{ u(t-a) \} = \int_{0}^{\infty}{e^{-st}u(t-a)dt} = \int_{0}^{a}{e^{-st}u(t-a)dt} +\int_{a}^{\infty}{e^{-st}u(t-a)dt} = $$ $$=\int_{0}^{a}{e^{-st}.0dt} +\int_{a}^{\infty}{e^{-st}.1dt} = \int_{a}^{\infty}{e^{-st}dt}= \left( – \frac{e^{-st}}{s} \right) _{a}^{\infty}=\frac{e^{-sa}}{s}$$
A função degrau unitário é particularmente importante no uso das transformadas de Laplace por causa da relação entre f(t) e sua translação g(t) = u(t-a)f(t-a) dada pelo teorema seguinte.
TEOREMA DA TRANSLAÇÃO: Se f(t) possui a transformada F(s), então a função $$\widetilde{f}(t) = f(t-a)u(t-a) = \left\{ \begin{array}{lll}
0 & ; & t<a\\
f(t-a)& ; & t\geq a\\
\end{array} \right.$$
possui transformada dada por e^{-as}F(s). Ou seja, se \mathscr{L}\{ f(t) \} = F(s), então $$\mathscr{L}\{ f(t-a)u(t-a) \} = e^{-as} F(s).$$ Consequentemente,
$$ f(t-a)u(t-a) = \mathscr{L}^{-1} \{e^{-as} F(s) \}.$$
EXEMPLO 1
Considere f(t) = 5 \sin{t}.
Daí, F(s) = \frac{5}{s^2+1} e a translação de f(t) em t=2 é dada por
$$f(t-2)u(t-2) = \left\{ \begin{array}{lll}
0 & ; & t<2\\
5\sin{(t-2)}& ; & t>2\\
\end{array} \right.$$
Pelo teorema acima, temos que $$\mathscr{L}\{ f(t-2)u(t-2) \} = e^{-2s}.\frac{5}{s^2 +1} = \frac{5e^{-2s}}{s^2 +1}$$
EXEMPLO 2
Considere a função definida por $$f(t) = \left\{ \begin{array}{rll}
\sin{t} & ; & t< \frac{\pi}{4} \\
\sin{t} + \cos{(t – \frac{\pi}{4})}& ; & t\geq \frac{\pi}{4}\\
\end{array} \right.$$
Temos que $$f(t) = \sin{t} + \left\{ \begin{array}{rll}
0 & ; & t< \frac{\pi}{4} \\
\cos{(t – \frac{\pi}{4})}& ; & t\geq \frac{\pi}{4}\\
\end{array} \right. = \sin{t} + u(t- \pi/4)\cos{t-\pi/4}.$$
Daí, $$\mathscr{L}\{ f(t) \} = \mathscr{L}\{ \sin{t} + u(t- \pi/4)\cos{t-\pi/4} \} = \mathscr{L}\{ \sin{t} \} + \mathscr{L}\{ u(t- \pi/4)\cos{t-\pi/4} \} $$ $$=\mathscr{L}\{ \sin{t} \}+ e^{-\pi s/4} \mathscr{L}\{ \cos{t} \} = \frac{1}{s^2 +1}+e^{-\pi s/4}\frac{s}{s^2+1}.$$
EXEMPLO 3
Encontre a inversa da transformada $$F(s) = \frac{1-e^{-2s}}{s^2}.$$
Observe que:
$$f(t) = \mathscr{L}^{-1} \left\{ \frac{1-e^{-2s}}{s^2} \right\} = \mathscr{L}^{-1} \left\{ \frac{1}{s^2} \right\}-\mathscr{L}^{-1} \left\{ \frac{e^{-2s}}{s^2} \right\} = \mathscr{L}^{-1} \left\{ \frac{1}{s^2} \right\}-\mathscr{L}^{-1} \left\{e^{-2s} \frac{1}{s^2} \right\}.$$ Pelo teorema anterior, $$f(t)= t – u(t-2)(t-2).$$
EXEMPLO 4
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Considere a função $$f(t) = \left\{ \begin{array}{rll}
2 & ; & 0 \leq t < 1 \\
\frac{1}{2} t^2 & ; & 1\leq t < \frac{\pi}{2}\\
\cos{t} & ; & t \geq \frac{\pi}{2}\\
\end{array} \right. .$$
Escreva-a em termos da função degrau unitário e encontre sua transformada de Laplace.
Temos que, $$f(t) = \left\{ \begin{array}{rll}
2 & ; & 0 \leq t < 1 \\
0 & ; & 1\leq t < \frac{\pi}{2}\\
0 & ; & t \geq \frac{\pi}{2}\\
\end{array} \right. + \left\{ \begin{array}{rll}
0 & ; & 0 \leq t < 1 \\
\frac{1}{2} t^2 & ; & 1\leq t < \frac{\pi}{2}\\
0 & ; & t \geq \frac{\pi}{2}\\
\end{array} \right. + \left\{ \begin{array}{rll}
0 & ; & 0 \leq t < 1 \\
0 & ; & 1\leq t < \frac{\pi}{2}\\
\cos{t} & ; & t \geq \frac{\pi}{2}\\
\end{array} \right. .$$
$$f(t) = 2 \left\{ \begin{array}{rll}
1 & ; & 0 \leq t < 1 \\
0 & ; & 1\leq t < \frac{\pi}{2}\\
0 & ; & t \geq \frac{\pi}{2}\\
\end{array} \right. + \frac{1}{2} t^2 \left\{ \begin{array}{rll}
0 & ; & 0 \leq t < 1 \\
1 & ; & 1\leq t < \frac{\pi}{2}\\
0 & ; & t \geq \frac{\pi}{2}\\
\end{array} \right. + \cos{t} \left\{ \begin{array}{rll}
0 & ; & 0 \leq t < 1 \\
0 & ; & 1\leq t < \frac{\pi}{2}\\
1 & ; & t \geq \frac{\pi}{2}\\
\end{array} \right. .$$
$$f(t) = 2 \left\{ \begin{array}{rll}
1 & ; & 0 \leq t < 1 \\
0 & ; & t \geq 1
\end{array} \right. + \frac{1}{2} t^2 \left\{ \begin{array}{rll}
0 & ; & 0 \leq t < 1 \\
1 & ; & 1\leq t < \frac{\pi}{2}\\
0 & ; & t \geq \frac{\pi}{2}\\
\end{array} \right. + \cos{t} \left\{ \begin{array}{rll}
0 & ; & t < \frac{\pi}{2}\\
1 & ; & t \geq \frac{\pi}{2}\\
\end{array} \right. .$$
Daí,
$$f(t) = 2(1-u(t-1)) + \frac{1}{2} t^2 \left\{ u(t-1) – u(t-\frac{\pi}{2})\right\} + \cos{(t)} u(t-\frac{\pi}{2})$$
Portanto, em termos da função degrau unitário
$$f(t) = 2-2u(t-1)) + \frac{1}{2} t^2 \left\{ u(t-1)\right\} – \frac{1}{2}t^2 \left\{u(t-\frac{\pi}{2})\right\} + \cos{(t)} u(t-\frac{\pi}{2})$$
A transformada de f(t) é dada por
\begin{eqnarray}
\mathscr{L} \left( f(t) \right) & = & \mathscr{L} (2) – \mathscr{L} \left(u(t-1))\right) + \frac{1}{2} \mathscr{L} \left(t^2 \left\{ u(t-1)\right\}\right) \\
\\
& & – \frac{1}{2}\mathscr{L} \left(t^2 \left\{u(t-\frac{\pi}{2})\right\}\right) + \mathscr{L} \left(\cos{(t)} u(t-\frac{\pi}{2})\right)\\
\\
& = & \frac{2}{s} – \frac{2e^-s}{s} + \frac{1}{2} \mathscr{L} \left(t^2 \left\{ u(t-1)\right\}\right) \\
\\
& & – \frac{1}{2}\mathscr{L} \left(t^2 \left\{u(t-\frac{\pi}{2})\right\}\right) + \mathscr{L} \left(\cos{(t)} u(t-\frac{\pi}{2})\right)\\
\end{eqnarray}
Agora é necessário escrever as funções t^2 e \cos{t } de maneira adequada para utilizarmos o teorema que relaciona a função e sua translação. Daí, devemos notar que:
\begin{eqnarray}
t^2 & = & t^2 +2at -2at +a^2 -a^2 \\ & = & (t-a)^2 +2at-a^2 \\ & = & (t-a)^2 +2at-2a^2 +2a^2 -a^2 = \\ & = & (t-a)^2 +2a(t-a) + a^2\\
\end{eqnarray}
Logo, \begin{eqnarray} t^2 & = & (t-1)^2+2(t-1)+1\\ t^2 & = & \left(t-\frac{\pi}{2}\right)^2 + \pi \left(t-\frac{\pi}{2}\right)+ \frac{\pi ^2}{4} \\ \cos{t} & = & \cos{\left( (t-\frac{\pi}{2})+\frac{\pi}{2} \right)} = -\sin{(t-\frac{\pi}{2})}
\end{eqnarray}
Vamos encontrar as transformadas de cada projeção:
\begin{eqnarray}
\frac{1}{2} \mathscr{L} \left(t^2 \left\{ u(t-1)\right\}\right) & = & \frac{1}{2} \mathscr{L} \left\{[(t-1)^2 +2(t-1) + 1)] u(t-1)\right\} \\
&= & \frac{1}{2}\mathscr{L}\left( (t-1)^2 u(t-1) \right)+ \\
& & +\mathscr{L}\left( (t-1) u(t-1) \right) + \frac{1}{2}\mathscr{L}\left( u(t-1) \right)\\
& = & \frac{1}{2} e^{-s} \frac{2!}{s^3}+ e^{-s} \frac{1}{s^2} + \frac{e^{-s}}{s}\\
& = & e^{-s} \left( \frac{1}{s^3}+ \frac{1}{s^2} + \frac{1}{2s} \right)
\end{eqnarray}
\begin{eqnarray}
\frac{1}{2}\mathscr{L} \left(t^2 \left\{u(t-\frac{\pi}{2})\right\}\right) & = & \frac{1}{2} \mathscr{L} \left\{ \left( (t-\frac{\pi}{2})^2 +\pi(t-\frac{\pi}{2}) + \frac{\pi ^2}{4} \right) u(t-\frac{\pi}{2}) \right\} \\
& = & \frac{1}{2} \mathscr{L} \left( (t-\frac{\pi}{2})^2 u(t-\frac{\pi}{2}) \right) + \frac{\pi}{2} \mathscr{L} \left((t-\frac{\pi}{2}) u(t-\frac{\pi}{2}) \right) + \\
& & + \frac{1}{2}\mathscr{L} \left (\frac{\pi ^2}{4} u(t-\frac{\pi}{2})\right) \\
& = & \frac{1}{2} e^{-\frac{\pi}{2}s} \frac{2!}{s^3}+ e^{-\frac{\pi}{2}s} \frac{\pi}{2s^2} + \frac{\pi ^2}{8} \frac{e^{-\frac{\pi}{2}s}}{s}\\
& = & e^{-\frac{\pi}{2}s} \left( \frac{1}{s^3}+ \frac{\pi}{2s^2} + \frac{\pi ^2}{8}\frac{1}{s} \right)
\end{eqnarray}
\begin{eqnarray}
\mathscr{L} \left(\cos{(t)} u(t-\frac{\pi}{2})\right) & = & – \mathscr{L} \left(\sin{(t-\frac{\pi}{2})} u(t-\frac{\pi}{2})\right)\\
& = & e^{-\frac{\pi}{2} s} \frac{1}{s^2 +1}
\end{eqnarray}
Portanto,
\begin{eqnarray}
\mathscr{L} \left( f(t) \right) & = & \frac{2}{s} – \frac{2e^-s}{s} + e^{-s} \left( \frac{1}{s^3}+ \frac{1}{s^2} + \frac{1}{2s} \right) – e^{-\frac{\pi}{2}s} \left( \frac{1}{s^3}+ \frac{\pi}{2s^2} + \frac{\pi ^2}{8}\frac{1}{s} \right) + e^{-\frac{\pi}{2} s} \frac{1}{s^2 +1} \\
\end{eqnarray}
Exercícios Resolvidos:
- Função Degrau Unitário | 1ª Lista de Exercícios Resolvidos
- Função Degrau Unitário | 2ª Lista de Exercícios Resolvidos
LEIA MAIS:
- Delta de Dirac e a Transformada de Laplace| Lista de Exercícios Resolvidos
- Transformada de Laplace Inversa | Lista de Exercícios Resolvidos
- Transformada de Laplace | Das Definições Básicas à Função Delta
- Solucionando Eq. Diferenciais Ordinárias Via Transformada de Laplace



Professor, uma dúvida. Se for uma função, por exemplo:
t² * {1; 2<= t 4 }
Como ficaria a transformada? Pois a u(t-a) é da forma: 0; t= a.
Obrigado professor, ótimo conteúdo.
Pingback: O Delta de Dirac | Da definição à solução de Equações Diferenciais
Pingback: Transformada de Laplace | 1ª Lista de Exercícios Resolvidos - Matemática Simplificada
Pingback: O que são Funções Pares e Funções Ímpares? | Pré-Cálculo
Pingback: Introdução às Funções Reais | Pré-Cálculo - Matemática Simplificada
Pingback: A Função Erro de Gauss ou Integral de Probabilidade