Introdução às Funções Reais | Pré-Cálculo

O objeto fundamental do cálculo são as funções reais. As funções surgem quando uma quantidade depende de outra. Por exemplo, a área A de um círculo depende de seu raio r. A lei que relaciona r com A é dada por A = \pi r^2, neste caso dizemos que A é uma função de r. Outros exemplos são, a população P de uma determinada espécie depende do tempo t, o custo C de envio de um pacote pelo correio depende de seu peso w.

Dados dois conjuntos A,B \neq \emptyset, uma função f de A em B (escrevemos f:A\rightarrow B) é uma lei ou regra que a cada x\in A, associa um único elemento f(x)\in B. Temos:

1. A é chamado domínio de f;
2. B é chamado contra-domínio de f;
3. o conjunto Im(f) = \left\{ y\in B\, ; \, y=f(x), \ x\in A \right\} é chamado imagem de f.

A natureza da regra que ensina como obter o valor f(x) quando é dado x \in A é inteiramente arbitrária, sendo sujeita apenas a duas condições:

1. A regra deve fornecer f(x) para todo x \in A.
2. A cada x \in A deve corresponder apenas um f(x) \in B.

EXEMPLO: A função f:\mathbb{N} \rightarrow \mathbb{Q} definida por f(n)=\dfrac{n}{n+1}, possui domínio igual a \mathbb{N} e contradomínio \mathbb{Q}.

Função Real – Definição e Primeiros Exemplos

DEFINIÇÃO [Função Real]: Uma função f é uma lei que associa cada elemento x do conjunto A, exatamente um elemento do conjunto B, denominado f(x).

Usualmente, consideramos que os conjuntos A e B são formados por números reais, onde A é denominado domínio e B é denominado contradomínio. Existe outro conjunto associado à função f.Este conjunto é a imagem de f, sendo denotada por $$\left\{y\in \mathbb{R}; y=f(x)\right\}.$$

Convenção: Se o domínio de uma função não é dado explicitamente, então, por convenção, adotamos como domínio o conjunto de todos os números reais x para os quais f(x) é um número real.

EXEMPLOS (Classes de Funções) Seja f:\mathbb{R} \rightarrow \mathbb{R}. Temos

1) função constante: f(x)=k;

2) função identidade: f(x)=x;

3) função linear: f(x)=ax;

4) função afim: f(x)=ax+b;

5) função polinomial: f(x)=a_0 +a_1x+a_2x^2+\cdots+a_nx^n=\sum_{i=0}^{n}a_ix_i ;em particular, se

1. n = 2 ,\, f(x) = ax^2 + b x + c é uma função
   quadrática,
2. se n = 3, \, f(x) = ax^3+ bx^2 + cx + d é uma função cúbica;

6) função potência: f(x) = x^a,\, onde a é uma constante; em particular, se a = \dfrac{1}{n} , f(x) = x^{1/n} = \sqrt[n]{x}, onde n é um inteiro positivo, é uma função raiz; temos que D_f = [0,+\infty) se n é par e D_f = \mathbb{R} se n é ímpar;

7) função racional: f(x)=\frac{p(x)}{q(x)}\ , onde p(x) e q(x) são funções polinomiais. Note que D_f = \{ x\in \mathbb{R}\,;\,q(x)\neq 0\};

8) função algébrica: função construída usando operações algébricas começando com polinômios; por exemplo,$$ f(x) = \sqrt{x^2+1},\, D_f = \mathbb{R},$$ $$g(x) = \frac{(x-4)}{x^4+\sqrt {2x}} \sqrt[3]{x+1}, \, D_g= 0,+\infty).$$

Funções com Domínios Restritos

Sejam f:A\rightarrow B e D\subset A. Denotamos por f\big|_{D} a restrição de f ao subconjunto D de A. Então $$ f\big|_{D}(x)=f(x),\quad \forall \;x\in D. $$

EXEMPLO (Função definida por várias sentenças): definida de forma diversa em diferentes partes de seu domínio; por exemplo, $$ (a) \ f(x) = \left\{\begin{array}{ll} 1-x & \mbox{ se } x \leq 1,\\ x^2 & \mbox{ se } x > 1;
\end{array} \right. \qquad  (b) \ g(x) = |x| = \left\{\begin{array}{ll} x & \mbox{ se } x \geq 0 ,\\ – x & \mbox{ se } x < 0. \end{array} \right. $$

O Gráfico de Uma Função Real

O gráfico de uma função f é dado pelo conjunto $$G(f) = \left\{ (x,y)\in\mathbb{R} ^2; y=f(x) \right\}.$$ Entretanto, sua real utilidade está em sua representação gráfica no plano cartesiano x0y, que esboça o conjunto dado pelos pares pares ordenados \left(x,f(x) \right) para todo x \in D_f.

Decorre da definição acima que G(f) é o lugar geométrico descrito
pelo ponto (x,f(x))\in\mathbb{R}\times\mathbb{R}, quando x percorre o domínio D_f. Observe que, por exemplo, uma circunferência não representa o gráfico de uma função pois teríamos duas imagens para cada ponto do seu domínio.

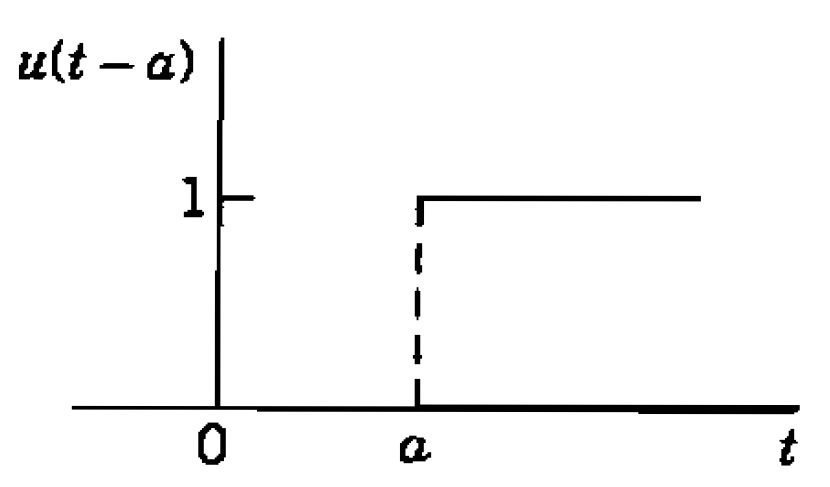
EXEMPLO [Função Degrau]: Também conhecida como Função de Heaviside, esta função é denotada por u(t-a) e dada por $$u(t-a) = \left\{ \begin{array}{lll} 0 & ; & t<a\\ 1& ; & t \geq a\\ \end{array} \right. \qquad a \geq 0.$$

FÓRMULAS DE TRANSLAÇÃO DO GRÁFICO:

1) f(x) + k translada o gráfico de f,\, k unidades para cima se k>0 e |k| unidades para baixo se k <0,;

2) f(x+ k) translada o gráfico de f,\, k unidades para a esquerda se k>0 e |k| unidades para a direita se k <0.

Operações Entre Funções Reais:

Dadas as funções f e g, é possível somar, multiplicar e dividir funções da seguinte forma:

1. (f \pm g)(x) = f(x)+g(x);
2. (f.g)(x) = f(x).g(x);
3. \left( \dfrac{f}{g} \right)(x) = \dfrac{f(x)}{g(x)}

Onde os domínios de (f \pm g)(x) e (f.g)(x) é a interseção dos domínios de f e g e o domínio de \left( \dfrac{f}{g} \right)(x) é a interseção do domínio de f com o domínio de g, excluindo-se os pontos que zeram g(x).

EXEMPLO: Se f(x) = \sqrt{7-x} e g(x) = \sqrt{x-2} , então D_f=(-\infty,7] ,\, D_g = [2, + \infty) e D_f \cap D_g = [2,7]. Temos que,

1. (f+g)(x) = \sqrt{7-x} + \sqrt{x-2}; \qquad 2 \leq x \leq 7,
2. (fg)(x) = \sqrt{7-x}\sqrt{x-2} = \sqrt{(7-x)(x-2)}; \qquad 2 \leq x \leq 7,
3. \Bigl(\dfrac{f}{g}\Bigr)(x) = \dfrac{\sqrt{7-x}}{\sqrt{x-2}} = \sqrt{\dfrac{7-x}{x-2}}; \qquad 2 < x \leq 7.

Composição de Funções

Dadas duas funções f e g, a função composta de g com f é denotada por g_Of(x), e é definida por $$g_o f (x) = g(f(x)).$$ Representação por diagrama da ideia de composição de funções:

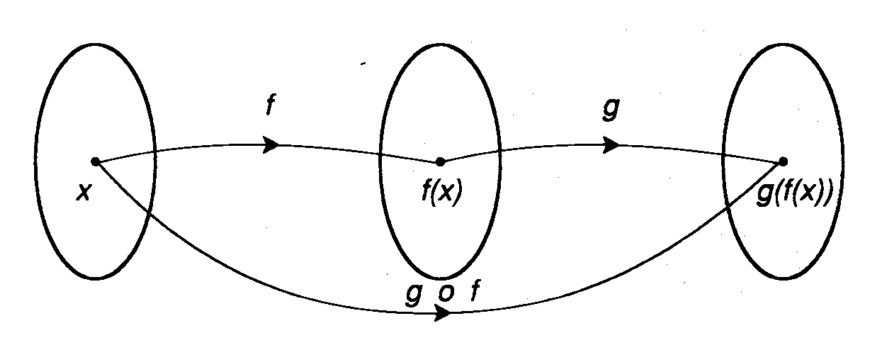
EXEMPLO: Se f(x) = 2x+1 e g(x) = x^2+3x , então

1. g \circ f (x) = g(2x+1) = (2x+1)^2+3(2x+1) = 4x^2 + 10x + 4;
2. f \circ g (x) = f(x^2+3x) = 2(x^2+3x) +1 = 2x^2 + 6x + 1.

OBSERVAÇÃO: Em geral, f\circ g \neq g \circ f.

EXEMPLO: Encontre f \circ g \circ h se f(x) = \dfrac{x}{x+1},\, g(x) = x^{10} e h(x) = x+3.

$$f \circ g \circ h(x) = f ( g (h(x))) = f(g(x+3)) = f((x+3)^{10}) = \frac{(x+3)^{10}}{(x+3)^{10}+1}.$$

Funções Inversas

Diremos que f:D_f \rightarrow B:

1. f é sobrejetora se, e somente se, Im(f)=B.
2. f é injetora se, e somente se, $$ f(x_1)=f(x_2)\Longrightarrow x_1=x_2,\;\textrm{para quaisquer}\;x_1,x_2\in D_f. $$
3. f é bijetora se, e somente se, f for injetora e sobrejetora.

Note que f será injetora se, e somente se, $$ x_1\neq x_2\Longrightarrow f(x_1)\neq f(x_2),\; \ \ \textrm{para quaisquer} \ \;x_1,x_2\in D_f.$$

EXEMPLO: A função módulo f(x)= |x| não é injetora pois, por exemplo,
|-1| = |1| e -1 \neq 1. f não é sobrejetora pois Im(f) =\mathbb{R}^+ \subset \mathbb{R}. Agora, considerando f\big|_{\mathbb{R}^+ }: \mathbb{R}^+ \Rightarrow \mathbb{R}^+ a função será bijetora.

OBSERVAÇÃO: Se tomamos B= Im(f) então f sempre será sobrejetora.

DEFINIÇÃO: Uma função f:A\to B será dita invertível, se existir g:B\toA (denotada por f^{-1}) tal que g\circ f=I_A e f\circ g = I_B.

PROPOSIÇÃO: Uma função f:A\to B será invertível se, e somente se, f for bijetora.

Neste caso, a função inversa está definida por f^{-1} (y)= x \mathbb{Q}quad \Longleftrightarrow \mathbb{Q}quad f(x) = y ,\quad \forall \, y \in B.

EXEMPLO A função f(x) = x^3 é injetora e a sua inversa é f^{-1}(x) = x^{1/3}.

OBSERVAÇÃO: f^{-1}(x) não significa \dfrac{1}{f(x)} = [f(x)]^{-1}.

COMO ACHAR A FUNÇÃO INVERSA?

1. Escreva y = f(x).
2. Resolva essa equação para x em termos de y.
3. Troque x por y para expressar f^{-1} como função de x.

EXEMPLO: Calcule f^{-1} para a função f(x)=1+3x.

SOLUÇÃO: Escrevemos y = 1 + 3x . Resolvemos para x, ou seja, x = \dfrac{ y-1}{3}. E substituindo y por x , obtemos $$f^{-1}(x) = \frac{x-1}{3}.$$

OBSERVAÇÃO: Note que $$G(f^{-1})=\left\{(y,f^{-1}(y)): y\in B\right\}=\left\{(f(x),x): x\in A\right\}\,.$$ Com isto, fica fácil verificar que G(f^{-1}) é a reflexão de G(f) em torno da reta y=x.

DEFINIÇÃO: Diremos que f é limitada se, e somente se, o conjunto \text{Im}(f) for limitado. Caso contrário, a função f será dita ilimitada. Se A_1\subset A, então f será limitada em A_1 se, e somente se, a restrição f|_{A_1} for limitada.

OBSERVAÇÃO: Segue da definição acima que se existir L>0 tal que |f(x)|\leq L, \quad \textrm{para todo}\;x\in D_f, ou, equivalentemente, se existirem L,\,l\in\mathbb R tais que l\leq f(x)\leq L,\quad\textrm{para todo}\;x\in D_f, então f será limitada.

EXEMPLO:

1. f(x)=\dfrac{x}{|x|} é limitada;
2. f(x)=\dfrac{x^4}{x^4+1} é limitada;
3. f(x) = \dfrac{1}{x} é ilimitada.

DEFINIÇÃO: Definimos:

1. \sup(f)=\sup\{f(x):x\in D_f\}.
2. \inf(f)=\inf\{f(x):x\in D_f\}.
3. Se \sup(f)=f(x_0) para algum x_0\in D_f, então diremos que f(x_0) é o máximo de f ou o valor máximo de f. O ponto x_0 será chamado ponto de máximo de f.
4. Se \inf(f)=f(x_0) para algum x_0\in D_f, então diremos que f(x_0) é o mínimo de f ou o valor mínimo de f. O ponto x_0 será chamado ponto de mínimo de f.

DEFINIÇÃO: Definimos:

1. Se valer a implicação x<y\Longrightarrow f(x)<f(y), então f será estritamente crescente.
2. Se valer a implicação x<y\Longrightarrow f(x)\leq f(y), então f será crescente.
3. Se valer a implicação x<y\Longrightarrow f(x)>f(y), então f será  estritamente decrescente.
4. Se valer a implicação x<y\Longrightarrow f(x)\geq f(y), então f será
   decrescente.

DEFINIÇÃO: Se f:A\Rightarrow B satisfizer uma das condições da definição acima diremos que f é uma função monótona ou monotônica.

EXEMPLO: f(x) = x^2 é estritamente crescente para x > 0 e estritamente decrescente para x<0.

EXEMPLO f(x) = \dfrac{x+1}{x} é estritamente decrescente.

OBSERVAÇÃO: Observe que se x < y então f(x) = 1 + \dfrac{1}{x} > 1+\dfrac{1}{y} = f(y).

Leia Mais:

• Números Reais | Definição, Operações Elementares, Intervalos e Módulo
• Função de Heaviside ou Degrau Unitário
• O Que São Funções Periódicas? Definição e Exemplos.
• O que são Funções Pares e Funções Ímpares?