Os Espaços Euclidianos R² e R³ | Norma, Distância, Retas e Planos

O Espaço euclidiano é um espaço em qualquer número finito de dimensões, no qual os pontos são designados por coordenadas (uma para cada dimensão) e a distância entre dois pontos é dada por uma fórmula de distância.

Esta é a única concepção de espaço físico por mais de 2.000 anos, e continua sendo a forma mais atraente e útil de modelar o mundo como ele é vivido. Embora os espaços não euclidianos, como os que emergem da geometria elíptica e da geometria hiperbólica, tenham levado os cientistas a uma melhor compreensão do universo e da própria matemática, o espaço euclidiano continua sendo o ponto de partida para seu estudo.

Os espaço euclidiano n-dimensional é o produto cartesiano de n fatores iguais a \mathbb{R}. Ou seja,

1.  \mathbb{R}^2 = \mathbb{R} \times \mathbb{R}. Pode ser geometricamente representado pelo plano cartesiano.
2. \mathbb{R}^3 = \mathbb{R} \times \mathbb{R} \times \mathbb{R}. Pode ser geometricamente representado pelo eixo tridimensional.

Um elemento do espaço \mathbb{R}^n é denominado vetor e um elemento x é representado pela n-upla x=(x_1, x_2, x_3, ..., x_n).

Operações Elementares no Espaço Euclidiano

Sejam x=(x_1, x_2, x_3, ..., x_n) e y=(y_1, y_2, y_3, ..., y_n) dois elementos quaisquer do espaço \mathbb{R}^n e \lambda um escalar qualquer.

Definimos:

1. x\pm y é um elemento do espaço \mathbb{R}^n e $$x\pm y = (x_1\pm y_1, x_2\pm y_2, x_3\pm y_3, …, x_n \pm y_n)$$
2. o produto do escalar de \lambda com o vetor x, denotado por \lambda x, é um elemento do espaço \mathbb{R}^n dado por $$\lambda x = (\lambda x_1, \lambda x_2, \lambda x_3+, …, \lambda x_n)$$
3. x=y \Leftrightarrow x_i = y_i para i=1,2,3,...,n

EXEMPLO

Sejam x=(-1,4, \frac{3}{2}), y=(1,0), z=(1,0, 1) e t=(2,1).

Assim, x+y é impossível de ser computado, y-t= (1-2, 0-1) = (-1, -1) e

x+z=(-1-1, 4-0,\frac{3}{2} -1 ) = (0, 4, \frac{1}{2}).

Norma

A norma do vetor x=(x_1, x_2, x_3, ..., x_n) é o número
\begin{equation}
\left\| x \right\| = \left\| (x_1, x_2, x_3, …, x_n) \right\| = \sqrt{x_1 ^2 + x_2 ^2 + … + x_n ^2}.
\end{equation}
Geometricamente, a norma representa o tamanho do vetor que tem origem em (0,0,0,0,0,...,0) e fim no ponto (x_1, x_2, x_3, ..., x_n).

PROPRIEDADES DA NORMA:

Dados os vetores no espaço \mathbb{R}^n, x=(x_1, x_2, x_3, ..., x_n), y=(y_1, y_2, y_3, ..., y_n), e z=(z_1, z_2, z_3, ..., z_n) e seja \lambda um escalar, então temos as seguintes propriedades:

1. \left\| x \right\| \geq 0
2. \left\| x \right\| = 0 \Leftrightarrow x = (0,0,0,...,0)
3. [/katex] \left \| \lambda x \right\| = | \lambda | \left\| x \right\|[/katex]
4. \left\| x.y \right\| \leq \left\| x \right\| . \left\| y \right\| (Desigualdade de Cauchy-Schwarz)
5. \left\| x+y \right\| \leq \left\| x \right\| + \left\| y \right\| (Desigualdade Triangular)

EXEMPLO:

Calcule a norma dos seguintes vetores

1. \|(1,2)\|= \sqrt{1^2 + 2^2}=\sqrt{1+4}=\sqrt{5}
2. \|(2,1,3)\|=\sqrt{2^2 + 1^2 + 3^2}=\sqrt{4+1+9}=\sqrt{14}

DISTÂNCIA

A distância entre dois pontos do espaço \mathbb{R}^n, x=(x_1, x_2, x_3) e y=(y_1, y_2, y_3) é dada por
\begin{eqnarray}
d(x,y) & = & \left\|x-y\right\| \\
& = & \sqrt{(x_1-y_1)^2 +(x_2-y_2)^2+…+ (x_n-y_n)^2 }
\end{eqnarray}

Como consequência das propriedades da norma podemos garantir que

1. A distância entre dois pontos no \mathbb{R}^n é maior que zero.
2. A distância entre dois pontos no \mathbb{R}^n será nula se, e somente se, os dois pontos forem iguais.

EXEMPLO

Calcule a distância entre os seguintes pontos.

1. A(1,1,1), B(3,3,3)
2. A(a,b,c\sqrt{2}), B(b,-a,0)
3. A(0,1), B(b,-a)

No primeiro item, temos que $$d(A,B) = \sqrt{(1-3)^2 +(1-3)^2+(1-3)^2 }=\sqrt{12} = 3\sqrt{2}$$

Já no segundo caso, $$d(A,B) = \sqrt{(a-b)^2+(b+a)^2+2}=\sqrt{2a^2+2b^2+2}$$.

Por fim, a terceira distância é dada por $$d(A,B) = \sqrt{b^2 +(1+a)^2}.$$

Produto Escalar

Dados dois vetores x=(x_1, x_2, x_3, ..., x_n) e y=(y_1, y_2, y_3, ..., y_n) no espaço \mathbb{R}^n, o número indicado por $$x.y=x_1.y_1+ x_2.y_2+ x_3.y_3+ …+ x_n.y_n$$ é chamado de produto escalar dos vetores x e y.

Podemos observar que o produto escalar entre dois vetores é um número real ao contrário do que acontecerá ao produto vetorial mais à frente.

EXEMPLO

1. O produto escalar dos vetores (2,3) e (1,5) é $$(2,3).(1,5)=2.1+3.5=17.$$
2. o produto escalar dos vetores (2,3-1) e (1,5,0) é $$(2,3,-1).(1,5,0)=2.1+3.5+(-1).0=17.$$
3. O produto escalar dos vetores (2,3) e (1,5,0) não pode ser computado.

Propriedades do Produto Escalar

Dados os vetores no espaço \mathbb{R}^n, x=(x_1, x_2, x_3, ..., x_n), y=(y_1, y_2, y_3, ..., y_n), e z=(z_1, z_2, z_3, ..., z_n) e seja \lambda um escalar, então temos as seguintes propriedades:

1. x.y = y.x (Comutatividade)
2. \left( x+y \right).z = x.z +y.z (Distributividade)
3. (\lambda x).y = x.(\lambda y)= \lambda (x.y)
4. x.x \geq 0;
5. x.x=0 \Leftrightarrow x = (0,0,0,...,0)
6. Dois vetores do espaço \mathbb{R}^n são perpendiculares se o produto escalar entre os dois for nulo.
7. O vetor 0 = (0,0,0,0,...,0) é perpendicular a qualquer outro vetor do espaço \mathbb{R}^n.

EXEMPLO:

1. Como o produto escalar dos vetores (2,3) e (1,5) é $$(2,3).(1,5)=2.1+3.5=17,$$ estes vetores não são perpendiculares.
2. Já os vetores (1,0,0) e (0,2,3) são perpendiculares.

Observações importantes

1. \left\| x \right\| = \left\| (x_1, x_2, x_3, ..., x_n) \right\| = \sqrt{x.x}
2. O ângulo \theta entre os vetores \stackrel{\rightarrow}{x} e \stackrel{\rightarrow}{y} é dado por $$\cos{\theta}=\dfrac{x.y}{\left\|x\right\| \left\|x\right\|}.$$
3. Se \theta é o ângulo entre os vetores \stackrel{\rightarrow}{x} e \stackrel{\rightarrow}{y}, então x.y = \left\|x\right\| \left\|x\right\| \cos{\theta}

Produto Vetorial

Sejam x=(x_1, x_2, x_3) e y=(y_1, y_2, y_3) dois vetores do \mathbb{R}^3.

O produto vetorial entre x e y é um vetor, denotado por x \wedge y e definido pelo determinante

\begin{equation}
x \wedge y = \left|
\begin{array}{ccc}
i & j & k \\
x_1 & x_2 & x_3\\
y_1 & y_2 & y_3
\end{array} \right|
\end{equation}
onde i=(1,0,0), j=(0,1,0) e k=(0,0,1)

Observações Importantes:

1. Se \theta é o ângulo entre os vetores \stackrel{\rightarrow}{x} e \stackrel{\rightarrow}{y}, então \left\|x \wedge y \right\| = \left\|x\right\| \left\|y\right\| \sin{\theta};
2. O produto vetorial x \wedge y é perpendicular a x e a y simultaneamente.

EXEMPLO

Calcule o produto vetorial entre os vetores (1,2,-1)= e (2,1,3)=.
$$\left|
\begin{array}{lcr}
i & j & k \\
1 & 2 & -1\\
2 & 1 & 3
\end{array} \right|=7i-5j-3k=(7, -5, -3)$$

Retas no Espaço Euclidiano R³

A equação da reta que passa pelo ponto x=(x_1, y_1, z_1), na direção do vetor u=(u_1, u_2, u_3) é dada por $$\left\{ \begin{array}{lll}
x & = & x_1 + t u_1\\
y & = & y_1 + t u_2\\
z & = & z_1 + t u_3\\
\end{array}
\right.$$ onde t \in \mathbb{R} é denominado parâmetro. Esta equação pode ser analogamente estendida ao \mathbb{R} ^2.

Observações

1. Quando apenas uma das componentes do vetor diretor da reta é nula, então esta reta é paralela ao plano determinado pelos eixos das duas componentes não nulas.
2. Se duas componentes do vetor diretor da reta são nulas então esta reta é paralela ao eixo correspondente à componente não nula.
3. O ângulo \theta entre duas retas r_1 e r_2 é o menor ângulo formado pelos seus vetores diretores v_1 e v_2 e pode ser encontrado pela relação: $$\cos{\theta} = \dfrac{|v_1 . v_2|}{\| v_1 \| \|v_2 \|}.$$
4. Duas retas são paralelas quando seus vetores diretores são paralelos. Uma condição de paralelismo entre duas retas r_1 e r_2 com vetores diretores v_1 = (a_1, b_1, c_1) e v_2 = (a_2, b_2, c_2) é que $$\dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2} $$
5. Duas retas r_1 e r_2 com vetores diretores v_1 = (a_1, b_1, c_1) e v_2 = (a_2, b_2, c_2) são ortogonais quando v_1 . v_2 = 0.

Planos no Espaço Euclidiano R³

A equação do plano que passa pelo ponto x=(x_1, y_1, z_1), e tem com vetor normal u=(a, b, c) é dada por
$$a x+b y + c z +d = 0,$$ onde d = -ax_1 - by_1 - cz_1.

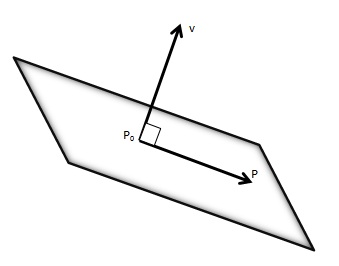
Observações:

1. Os três coeficientes a,b e c da equação geral ax+by+cz+d=0 representam as componentes de um vetor normal ao plano.
2. Se, na equação geral do plano, d=0, então o plano passa pela origem.
3. Se apenas uma das componentes do vetor normal ao plano é nula, então o plano é ortogonal a um dos eixos coordenados e paralelo ao eixo corresponde à coordenada nula.
4. Se duas componentes do vetor normal ao plano são nulas, então o plano é ortogonal ao eixo correspondente à componente não nula e paralelo ao plano formado pelas outras duas componentes.
5. O ângulo entre dois planos é o menor ângulo formado por seus vetores normais.
6. Dois planos são paralelos se seus vetores normais são paralelos. Se os dois vetores normais forem ortogonais, então os planos serão ortogonais.

EXEMPLO

O plano de equação x+3y+2z-6 = 0 é perpendicular ao vetor v=(1,3,2) e passa pelos pontos (6,0,0), (0,2,0) e (0,0,3).

A equação deste plano ainda pode ser escrita em sua forma vetorial utilizando dois vetores diretores (0,2,0) - (6,0,0) = (-6,2,0) e [/katex] (0,0,3) – (6,0,0) = (-6, 0, 3)[/katex] e o ponto (6,0,0) da seguinte maneira: $$(x,y,z) = (6,0,0)+\lambda (-6,2,0) + \gamma (-6,0,3)$$

Note que o vetor normal ao plano deve ser ortogonal a (-6,2,0) e (-6,0,3), simultaneamente.

Este vetor normal é encontrado pelo produto vetorial $$(-6,2,0) \wedge (-6,0,3) = \left|
\begin{array}{ccc}
i & j & k \\
-6 & 2 & 0\\
-6 & 0 & 3
\end{array}
\right| = (6,18,12) = 6(1,3,2),$$ ou seja, obtemos um vetor paralelo ao vetor normal original.

EXEMPLO
Considere dois planos x+2y-3z -10 = 0 e 2x+3y-4z+7 = 0.

Seus respectivos vetores normais são v_1 = (1,3,-3) e v_2 = (2,3,-4).

O ângulo entre os dois planos é dado por $$\cos{\theta} = \dfrac{|v_1 . v_2|}{\| v_1 \| \|v_2 \|} = \dfrac{20}{\sqrt{406}},$$ isto é, \theta = arccos\left( \dfrac{20}{\sqrt{406}} \right) \approx \dfrac{61}{50} \pi.

EXEMPLO

Vamos encontrar a interseção entre os planos x-2y+z-1 = 0 e 3x+y-2z-3 =0.

Neste caso, temos que $$\left\{
\begin{array}{ccc}
x-2y+z-1 & = & 0\\
3x+y-2z-3 & = & 0\\
\end{array} \right.$$ que, por escalonamento, nos dá $$x=1+\dfrac{3}{7}z$$ $$y=\dfrac{5}{7}.$$

Fazendo z = \lambda temos que a interseção destes dois planos é a reta de equações paramétricas:
$$\left\{
\begin{array}{ccc}
x & = & 1+\dfrac{3}{7}\lambda\\
y & = & \dfrac{5}{7}\lambda\\
z & = & \lambda
\end{array}
\right.
$$

Podemos conluir que a reta resultante da interseção dos dois planos é a que passa pelo ponto (1,0,0) na direção do vetor \left( \dfrac{3}{7} , \dfrac{5}{7},1 \right).

Observação:

Existe uma outra maneira de encontrar a direção da reta interseção entre dois planos.

Dados dois planos com vetores normais v e u, o vetor resultante do produto vetorial u \wedge v é o vetor diretor da reta interseção entre os planos.

Os Espaços Euclidianos R² e R³ – Listas de Exercícios Resolvidos

• Os Espaços Euclidianos R² e R³ – 1ª Lista de Exercícios Resolvidos
• Os Espaços Euclidianos R² e R³ | 2ª Lista de Exercícios Resolvidos
• Os Espaços Euclidianos R² e R³ | 3ª Lista de Exercícios Resolvidos

Leia Mais:

• Curvas no Espaço | Parametrização, Comprimento de Arco e Deslocamento de Partícula
• Problemas do Milênio | Os 7 Problemas de Matemática para o Século XXI
• Curvas no Espaço | Funções de uma Variável Real a Valores Vetoriais
• Campos Vetoriais | Definição, Exemplos, Rotacional e Divergente

Assista nossa vídeo-aula sobre Espaços Euclidianos: