Os Espaços Euclidianos R² e R³ | 3ª Lista de Exercícios Resolvidos

Neste artigo queremos apresentar uma terceira lista de exercícios resolvidos envolvendo objetos matemáticos comuns a espaços euclidianos construídos sobre o corpo dos números reais, como retas, planos e pontos e particularidades inerentes a estes conceitos.

Os Espaços Euclidianos R² e R³ – 3ª Lista de Exercícios Resolvidos

1) Encontre a reta interseção entre os planos de equações x+y+z-3 = 0 e x+y-z+1=0.

SOLUÇÃO: Os pontos de interseção dos planos são aqueles onde as duas equações se igualam em suas soluções. Com isso, igualando as duas equações, obtemos, por eliminação de x+y , $$z-3 = -z +1 \Leftrightarrow z = 2. $$

Substituindo este valor nas equações dos planos encontramos $$x+y-1 = 0; \qquad z = 2 .$$ Ou seja, a reta interseção dos planos do enunciado é também a interseção dos planos x + y -1 = 0 e z = 2 . Fazendo x = t na primeira equação encontramos a reta de equação $$s:\left\{ \begin{array}{lll} x & = & t\\ y & = &1 -t\\ z & = & 2\\ \end{array} \right. ; \qquad t \in \mathbb{R} $$ que a reta que passa pelo ponto (0,1,2) na direção do vetor \vec{u} = (1,-1,0). .

Observação: Neste exercício, pode-se encontrar equações diferentes para a mesma reta se acordo com a escolha de quais variáveis eliminar no primeiro passo. Lembre-se que, em particular, uma reta pode ser representada por vários tipos de equações paramétricas.

2) Demonstre que a distância de um ponto P_0 = (x_0, y_0, z_0) a um plano de equação \pi : ax+by+cz+d=0 é dada por $$ d( \pi, P_0 ) = \frac{|ax_0 + by_0 + cz_0 +d|}{\sqrt{a^2 + b^2 + c^2}}$$

SOLUÇÃO: Sejam um ponto P_0(x_0, y_0, z_0) e um plano \pi no espaço $$ \pi: \ ax+by + cz + d = 0.$$ Seja o ponto A o pé da perpendicular conduzida pelo ponto P_0 sobre o plano \pi e seja P(x,y,z) um ponto qualquer pertencente a \pi.

Se um vetor \overrightarrow{n}=(a,b,c) é normal ao plano \pi, então o vetor \overrightarrow{AP_0} tem a mesma direção de \overrightarrow{n}. A distância d do ponto P_0 ao plano \pi é dada por: $$ d(P_0,\pi) = \left \| \overrightarrow{AP_0} \right \| $$
O vetor \overrightarrow{AP_0} é a projeção ortogonal do vetor \overrightarrow{PP_0} sobre \pi na direção de \overrightarrow{n}: $$ \text{Proj}_{\displaystyle \overrightarrow{v}}\overrightarrow{u} = \left ( \frac{\overrightarrow{u} \cdot \overrightarrow{v}}{\overrightarrow{v}\cdot \overrightarrow{v}} \right )\cdot \overrightarrow{v} $$
Aplicando ao nosso problema, temos que: $$ d(P_0,\pi) = \left | AP_0 \right | \\ \ \\ d(P_0,\pi) = \left \| \frac{\overrightarrow{PP_0}\cdot \overrightarrow{n}}{\left \| \overrightarrow{n} \right \|^2} \cdot \overrightarrow{n} \right \|\\ \ \\ d(P_0,\pi) = \frac{\left | \overrightarrow{PP_0}\cdot \overrightarrow{n} \right |\ \left \| \overrightarrow{n} \right \| }{\left \| \overrightarrow{n} \right \|^2}\\ $$

O que nos leva a: $$ d(P_0,\pi) = \frac{\left | \overrightarrow{PP_0}\cdot \overrightarrow{n} \right |}{\left \| \overrightarrow{n} \right \|} $$

No entanto, temos que: $$ \overrightarrow{PP_0} = (x_0-x, y_0-y, z_0-z) $$ E que: $$ \overrightarrow{n} = (a,b,c) $$ E ainda: $$ \left \| \overrightarrow{n} \right \| = \sqrt{a^2+b^2+c^2}$$

Substituindo estes resultados em $$ d(P_0,\pi) = \frac{\left | \overrightarrow{PP_0}\cdot \overrightarrow{n} \right |}{\left \| \overrightarrow{n} \right \|} $$ obtemos

$$ d(P_0,\pi) = \frac{\left | (x_0-x,y_0-y, z_0-z) \cdot (a,b,c) \right |}{\sqrt{a^2+b^2+c^2}}\\
\ \\ d(P_0,\pi) = \frac{\left | a(x_0-x), b(y_0-y), c(z_0-z) \right |}{\sqrt{a^2+b^2+c^2}} $$

Encontramos: $$ d(P_0,\pi) = \frac{\left | ax_0+by_0+cz_0-ax-by-cz \right |}{\sqrt{a^2+b^2+c^2}}.$$ Mas, isolando d da equação \pi: \ ax+by + cz + d = 0 temos $$ d = -ax-by-cz $$ Assim, $$ d(P_0,\pi) = \frac{\left | ax_0+by_0+cz_0+d \right |}{\sqrt{a^2+b^2+c^2}} $$

3) Determine as equações dos dois planos que distam 3 unidades do plano de equação 3x-y-z+1 = 0 e paralelos a este plano.

SOLUÇÃO: Usando a fórmula demonstrada no item anterior, obtemos que os dois planos que distam 3 unidades do plano de equação 3x-y-z+1 = 0 e paralelos a este plano satisfazem a relação.  $$ 3 = \frac{\left | 3x-y-z+1\right |}{\sqrt{3^2+(-1)^2+(-1)^2}} .$$ Ou seja, $$ 3 \sqrt{11} = \left | 3x-y-z+1\right |.$$ Desta forma, $$ \pi _1 : 3x-y-z+1 = 3 \sqrt{11} \Leftrightarrow \pi _1 : 3x-y-z+(1 – 3 \sqrt{11}) = 0$$ $$ \pi _2 : 3x-y-z+1 = – 3 \sqrt{11} \Leftrightarrow \pi _2 : 3x-y-z+(1 + 3 \sqrt{11}) = 0$$ são as equações dos planos.

4) Calcule o produto vetorial entre os vetores:

a) \vec{u} = (2,4,5) e \vec{v} = (4,3,2)

SOLUÇÃO: \begin{equation}
\vec{u} \wedge \vec{v} = \left|
\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
2 & 4 & 5\\
4 & 3 & 2
\end{array} \right| = -7 \vec{i} +16 \vec{j} -10 \vec{k} = (-7,16,-10).
\end{equation}

b) \vec{a} = (-2,3,2) e \vec{b} = (3,-5,-4)

SOLUÇÃO: \begin{equation}
\vec{u} \wedge \vec{v} = \left|
\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
-2 & 3 & 2\\
3 & -5 & -4
\end{array} \right| = -2 \vec{i} -2 \vec{j} +\vec{k} = (-2,-2,1).
\end{equation}

5) Determine a equação vetorial da reta que passa pelo ponto (1,2,-1) e que seja perpendicular às direções dos vetores \vec{u} = (1,1,1) e \vec{v} = (1,-2,1).

SOLUÇÃO: A equação vetorial da reta que passa pelo ponto (1,2,-1) e que seja perpendicular às direções dos vetores \vec{u} = (1,1,1) e \vec{v} = (1,-2,1). é dada por: $$r: (x,y,z) = (1,2,-1) + t ( \vec{u} \wedge \vec{v} ); \qquad t \in \mathbb{R} .$$

Facilmente calcularmos $$\vec{u} \wedge \vec{v} = \left|
\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
1 & 1 & 1\\
1 & -2 & 1
\end{array} \right| = 3 \vec{i} -3\vec{k} = (3,0,-3).$$

Portanto, $$r: (x,y,z) = (1,2,-1) + t (3,0,-3); \qquad t \in \mathbb{R} .$$

6) Considere um ponto no plano P_0 (x_0 , y_0) e um vetor \vec{v} = (m,n).

a) Escreva as equações paramétricas da reta que passa pelo ponto P_0 e tem como vetor diretor \vec{v}.

SOLUÇÃO: Esta é uma reta dada no plano. Desta forma, as equações paramétricas desta reta são dadas por $$s:\left\{ \begin{array}{lll}
x & = & x_0 + m t\\
y & = &y_0 + n t\\
\end{array} \right. \qquad t \in \mathbb{R}
$$

b) Escreva a equação geral desta mesma reta.

SOLUÇÃO: Irei apresentar a solução deste problema de três maneiras diferentes.

(1º Modo de Resolver) Supondo m \neq 0 , obtemos, da primeira equação paramétrica que $$t = \frac{x-x_0}{m}.$$ Substituindo na segunda equação paramétrica, obtemos $$y = y_0 + \left( \frac{x-x_0}{m} \right) n = y_0 + \frac{n}{m} \left( x-x_0 \right),$$ ou seja, $$y – y_0 = \frac{n}{m} \left( x-x_0 \right), $$ que é uma forma de escrever equação geral da reta, afinal, esta equação pode ser reescrita como $$nx – my + \left( m y_0 – n x_0 \right) = 0$$, e considerando c = m y_0 - n x_0 , obtemos $$nx – my + c = 0,$$ que é exatamente a equação geral da reta no plano. Observe que se m = 0 então o vetor diretor da reta é paralelo ao eixo y e a reta é vertical, paralela ao eixo y e cortando o eixo x em x = x_0 . Logo, a equação geral da reta neste caso é dada por x = x_0

(2º Modo de Resolver) A equação geral pode ser obtida através da equação reduzida da reta no plano, dada por $$y = a x + b, $$ onde a é a tangente do ângulo de inclinação \theta da reta em relação ao eixo x . Esta inclinação é a mesma do vetor diretor da reta \vec{v} = (m,n) com relação ao eixo x .

Por isso, sem perda de generalidade podemos considerar um vetor igual ao vetor \vec{v} = (m,n) com sua origem na origem do plano cartesiano, como na figura abaixo:

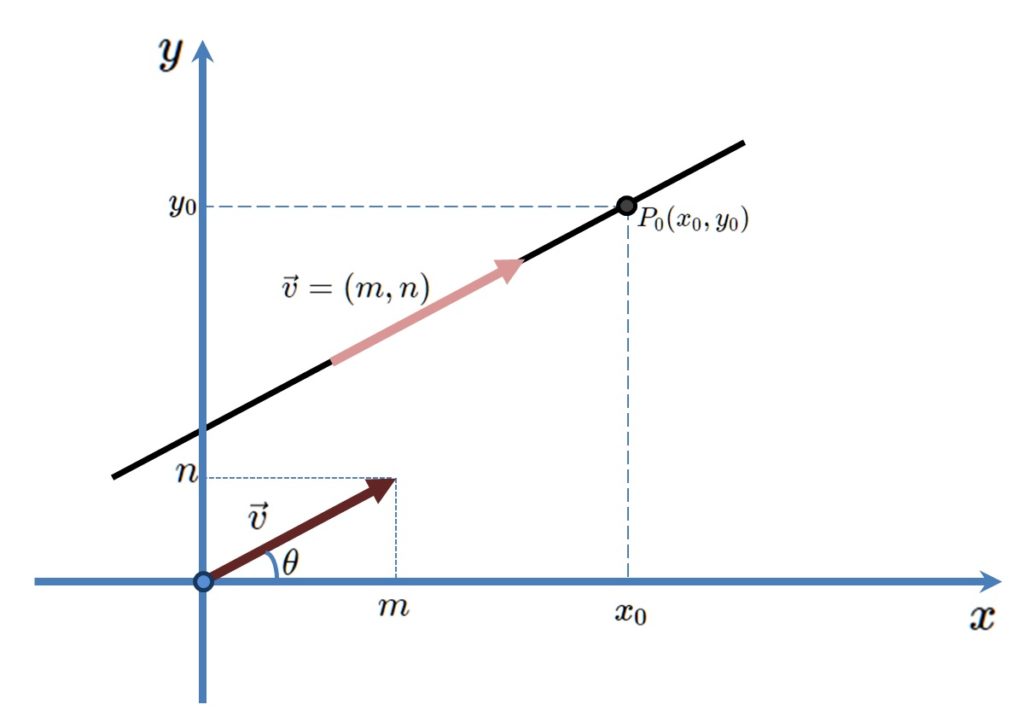
Deste modo, por trigonometria do triângulo retângulo, obtemos a = \tan{( \theta )} = \dfrac{n}{m} , sempre que m \neq 0 . Com isso, a equação reduzida desta reta é dada por $$y = \frac{n}{m} x + b .$$

Como o ponto P_0 (x_0 , y_0) satisfaz a equação da reta, podemos encontrar $$y_0 = \frac{n}{m} x_0 + b \Leftrightarrow b = y_0 – \frac{n}{m} x_0 \Leftrightarrow y = \frac{n}{m} x + \left( y_0 – \frac{n}{m} x_0 \right) .$$ O que nos leva a $$ y – y_0 = \frac{n}{m} \left(x – x_0 \right)$$ que é uma forma da equação geral da reta. O caso em m = 0 segue o mesmo do modo anterior.

(3º Modo de Resolver) Sabemos, pelo modo anterior que equação geral pode ser obtida através da equação reduzida da reta no plano, dada por $$y = a x + b, $$ onde a = \tan{( \theta )} = \dfrac{n}{m} , sempre que m \neq 0 . Com isso, a equação reduzida desta reta é dada por $$y = \frac{n}{m} x + b .$$ Agora, observe que: $$y = \frac{n}{m} x + b \Leftrightarrow nx -my +b = 0$$ que é a forma da equação geral da reta no plano, neste caso com b = my_0 - n x_0 . . O caso em m = 0 segue o mesmo do modo do primeiro método.

Leia Mais:

• Os Espaços Euclidianos R² e R³ | Norma, Distância, Retas e Planos
  
• Os Espaços Euclidianos R² e R³ | 1ª Lista de Exercícios Resolvidos
• Os Espaços Euclidianos R² e R³ | 2ª Lista de Exercícios Resolvidos
• Problemas do Milênio | Os 7 Problemas de Matemática para o Século XXI
  

Assista nossa vídeo-aula sobre Espaços Euclidianos: