E.D.O.’s de 2ª Ordem: Método dos Coeficientes Indeterminados (ou à Determinar)

Nesse artigo queremos apresentar o Método dos Coeficientes Indeterminados, também conhecido como o Método dos Coeficientes à Determinar, para solucionar EDO’s de segunda ordem da forma y'' +by'+cy = f(t), que são EDO’s lineares, não-homogêneas com coeficientes constantes e f é definida e contínua em um intervalo I.

Se f for identicamente nula então teremos um EDO homogênea de segunda ordem e com os coeficientes contantes, cuja forma de solução foi apresentada nesse outro artigo.

Neste caso buscamos soluções na forma:

A solução geral da equação homogênea associada é encontrada de forma direta como vimos nesse outro artigo.

O nosso atual problema consiste em encontrar uma solução particular para a equação y'' + by'+cy = f(t).

Para encontrar a solução particular da EDO completa usaremos uma técnica conhecida como Método dos Coeficientes Indeterminados para encontrar a parcela y_p (t) da solução geral.

O Método da Variação dos Parâmetros é uma técnica mais robusta e é discutida de forma mais geral nesse artigo.

MÉTODO DOS COEFICIENTES INDETERMINADOS (OU Método dos Coeficientes à Determinar)

Este método consiste em uma hipótese inicial sobre a forma da solução particular y_P (t) da estrutura abaixo , mas com os coeficientes não especificados:

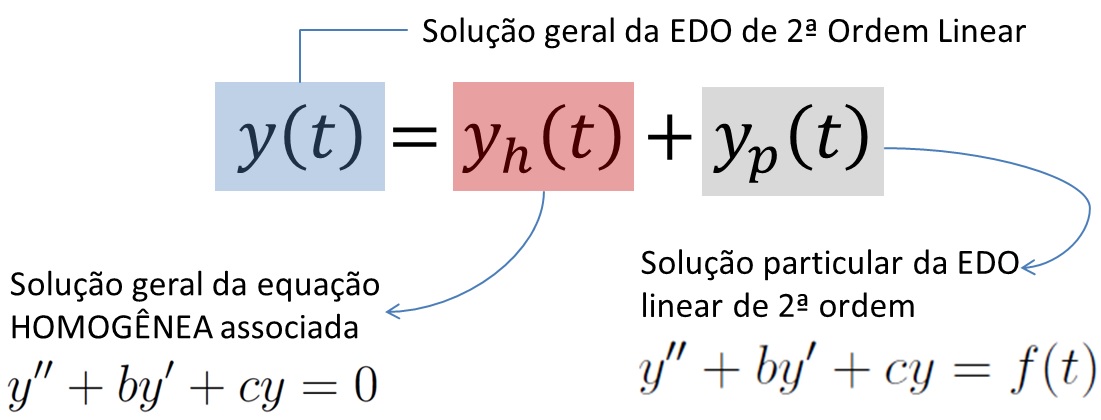
Daí substituímos a solução hipotética na EDO original e determinamos os coeficientes. Por fim, basta somarmos esta solução particular, y_P(t), com a solução da equação homogênea associada, y_H (t), que teremos uma solução geral para a EDO y'' + by'+cy = f(t).

Num primeiro momento, nossas funções f(t) serão apenas funções contínuas em todo o conjunto real, como:

• Trigonométricas;
• Exponenciais
• Polinômios;

Para ajudar a escolher uma foram geral de f(t), usamos a tabela abaixo:

EXEMPLO: Determine a solução geral de y'' + 3y'+2y = t.

• Equação Homogênea Associada: y'' + 3y'+2y = 0,  que possui equação característica dada por r^2 + 3r'+2 = 0,  que possui raízes dadas por \lambda _1 = -2\;\;\;\;\;\;\;\;\lambda_2 = -1. Assim, encontramos uma solução y_H (t) = c_1 e^{-2t} + c_2 e^{-t}
• Solução Particular: Uma solução particular de y'' + 3y'+2y = t deve ser da forma y_P (t) = mt+n.

Assim, substituindo na EDO:

Logo, 2m = 1 e (2n+3m)=0. Ou seja, m=1/2 e n=-3/4

Portanto y_P (t) = \dfrac{1}{2}t-\dfrac{3}{4}.

• Solução Geral: y(t) = y_H (t) + y_P (t)= c_1 e^{-2t} + c_2 e^{-t}+ \dfrac{1}{2}t-\dfrac{3}{4}

EXEMPLO: Determine a solução geral de y'' + 4y'+4y = e^{3t}.

• Equação Homogênea Associada: y'' + 4y'+4y = 0, que possui equação característica dada por r^2 + 4r+4 = 0, que possui raízes dadas por \lambda _1 = -2=\lambda_2. Assim, encontramos uma solução y_H (t) = c_1 e^{-2t} + c_2 t e^{-2t}
• Solução Particular: Uma solução particular de y'' + 4y'+4y = e^{3t} deve ser da forma y_P (t) = me^{3t}.

Basta uma olhada na tabela acima e notar que neste caso α=3. Logo, α não é raiz da equação característica.

Assim, (me^{3t})'' + 4(me^{3t})'+2(me^{3t}) = e^{3t}

\Rightarrow 9me^{3t} + 12 me^{3t} + 4 e^{3t} = e^{3t}

\Rightarrow 25m = 1 \Rightarrow m = \dfrac{1}{25}

\Rightarrow y_P (t) = \dfrac{1}{25} e^{3t}.

• Solução Geral: y(t) = y_H (t) + y_P (t)= c_1 e^{-2t} + c_2 t e^{-2t}+ \dfrac{1}{25}e^{3t}

EXEMPLO: Determine a solução geral de  y′′+4y′+4y= e^{-2t}

• Equação Homogênea Associada: y'' + 4y'+4y = 0, que possui equação característica dada por r^2 + 4r+4 = 0, que possui raízes dadas por \lambda _1 = -2=\lambda_2. Assim, encontramos uma solução y_H (t) = c_1 e^{-2t} + c_2 t e^{-2t}
• Solução Particular: Uma solução particular de y'' + 4y'+4y = e^{3t} deve ser da forma y_P (t) = mt^{2}e^{-2t}.

Basta uma olhada na tabela acima e notar que agora α é raiz dupla da equação característica para se certificar disso.

Agora basta substituir na EDO e encontrar o valor de m. Deixamos para o leitor encontrar a solução particular e a geral desta EDO.

EXEMPLO: Determine a solução geral de y'' + 4y'+4y = \sin{2t}

• Equação Homogênea Associada: y'' + 4y'+4y = 0, que possui equação característica dada por r^2 + 4r'+4 = 0, que possui raízes dadas por \lambda _1 = -2=\lambda_2. Assim, encontramos uma solução y_H (t) = c_1 e^{-2t} + c_2 t e^{-2t}
• Solução Particular: Uma solução particular de y'' + 4y'+4y = \sin{2t} deve ser da forma y_P (t) = m\cos{2t} + n \sin{2t}.

Basta uma olhada na tabela acima e notar que neste caso b é diferente de zero.

Assim, (m\cos{2t} + n \sin{2t})'' + 4(m\cos{2t} + n \sin{2t}) + 4 (m\cos{2t} + n \sin{2t}) =

=-8m \sin{2t} + 8n\cos{2t} =\sin{2t}

 \Rightarrow m=-\dfrac{1}{8}\;\;\;e\;\;\;n=0 \Rightarrow y_P (t) = - \dfrac{1}{8} \cos{2t}.

• Solução Geral: y(t) = y_H (t) + y_P (t)= c_1 e^{-2t} + c_2 t e^{-2t}- \dfrac{1}{8} \cos{2t}

EXEMPLO: Determine a solução geral de y′′+4y=sen(2t)

• Equação homogênea associada: y′′+4y= 0.

Obtemos a equação característica r² + 4 = 0, que tem raízes iguais a r = ±2i.

Logo,  y_H (t)=c_1 cos(2t)+c_2sen(2t) 

• Solução Particular: Como b é igual a zero e sen(2t) faz parte da solução homogênea, então y_P (t)=mtcos(2t)+ntsen(2t).

Agora basta substituir na EDO e encontrar o valor de m. Deixamos para o leitor encontrar a solução particular e a geral desta EDO.

MÉTODO DOS COEFICIENTES INDETERMINADOS (OU À DETERMINAR) – EXERCÍCIOS RESOLVIDOS

• Coeficientes Indeterminados | 1ª Lista de Exercícios Resolvidos
• Coeficientes Indeterminados | 2ª Lista de Exercícios Resolvidos
• Coeficientes Indeterminados | 3ª Lista de Exercícios Resolvidos
• Coeficientes Indeterminados | 4ª Lista de Exercícios Resolvidos

Leia Mais:

• Equações Diferenciais Ordinárias de 2ª Ordem, Homogêneas, com Coeficientes Constantes
• Equações Diferencias Ordinárias de 2ª Ordem: Equações Homogêneas
• Equações Diferencias Ordinárias de 2ª Ordem: O Princípio da Superposição
• Variação dos Parâmetros: EDOs de 2ª Ordem Lineares

Assista Nossa Vídeo-Aula: