Campos Escalares, ou Funções de Várias Variáveis a Valores Vetoriais, em geral são funções na forma f: A \subset \mathbb{R} ^n\rightarrow \mathbb{R}, que associa a cada n-upla de \mathbb{R} ^n um escalar. Nesse artigo queremos estabelecer o conceito de Derivada Direcional para esse tipo de função.
Vamos apresentar esse conceito através de funções com domínio no \mathbb{R} ^2 simplesmente pela facilidade em estabelecer gráficos e representações do domínio, e também por serem as funções que mais aparecem em aplicações de engenharia, por exemplo.
A Derivada Direcional
Sejam z = f(x,y) uma função, ( x_0 , y_0 ) em ponto do domínio desta função e \vec{u} = (a,b) um vetor unitário.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
DEFINIÇÃO (Derivada Direcional):
O limite $$ \frac{ \partial f}{ \partial \vec{u}} (x_0 , y_0 ) = \lim_{t \rightarrow 0}{\frac{f(x_0 + at , y_0 + bt) – f(x_0 , y_0 )}{t}}$$ quando existe e é finito, denomina-se derivada direcional de f no ponto ( x_0 , y_0 ) e na direção do vetor \vec{u} = (a,b) , sendo este um vetor unitário.
A derivada direcional \dfrac{ \partial f}{ \partial \vec{u}}(x_0 , y_0) denomina-se, também, taxa de variação de f no ponto (x_0 , y_0) e na direção do vetor \vec{u} .
EXEMPLO
Seja f(x,y) = x^2 + y^2 . Calcule \dfrac{ \partial f}{ \partial \vec{u}}(1,1) , onde \vec{u} = (a,b) é um vetor unitário qualquer.
Neste caso, $$ \frac{ \partial f}{ \partial \vec{u}} (1 ,1 ) = \lim_{t \rightarrow 0}{\frac{f(1 + at , 1 + bt) – f(1 , 1 )}{t}} = $$ $$ = \lim_{t \rightarrow 0}{\frac{(1 + at)^2 + (1 + bt)^2 -2}{t}} = 2 a + 2b.$$
Portanto, $$ \frac{ \partial f}{ \partial \vec{u}} (1 ,1 ) = 2 a + 2b.$$
EXEMPLO
Seja \vec{u} = (a,b) um vetor unitário dado. Vamos calcular \dfrac{ \partial f}{ \partial \vec{u}} (0,0 ) onde \begin{equation} f(x,y) = \left\{ \begin{array}{rll}
\frac{x^3}{x^2+y^2} ; (x,y) & \neq & (0,0)\\
\\
0; (x,y) & = & (0,0) \end{array} \right. .\end{equation}
Note que $$ \frac{f(0+at, 0 + bt) – f(0,0)}{t} = \frac{a^3 t^3}{t (a^2 t^2 + b^2 t^2)} = \frac{a^3}{a^2 + b^2} ; \;\;\; t \neq 0.$$
Como \vec{u} = (a,b) é um vetor unitário, então \| \vec{u} \| = a^2 + b^2 =1. Logo $$ \frac{f(0+at, 0 + bt) – f(0,0)}{t} = \frac{a^3}{a^2 + b^2} = a^3; \;\;\; t \neq 0.$$
Assim, $$ \frac{ \partial f}{ \partial \vec{u}} (0,0 ) = \lim_{t \rightarrow 0}{\frac{f(0+at, 0 + bt) – f(0,0)}{t} } = \lim_{t \rightarrow 0}{a^3} = a^3 . $$
Portanto, para todo vetor unitário \vec{u} = (a,b) $$ \frac{ \partial f}{ \partial \vec{u}} (0,0 ) = a^3 . $$
OBSERVAÇÕES:
1) Podemos observar que as derivadas parciais de f no ponto (x_0 , y_0) , são particulares derivadas direcionais:
$$ \frac{ \partial f}{ \partial \vec{i}} (x_0 , y_0 ) = \lim_{t \rightarrow 0}{\frac{f(x_0 + t , y_0) – f(x_0 , y_0 )}{t}} = \frac{ \partial f}{ \partial x} (x_0 , y_0 )$$
$$ \frac{ \partial f}{ \partial \vec{j}} (x_0 , y_0 ) = \lim_{t \rightarrow 0}{\frac{f(x_0 , y_0 + t) – f(x_0 , y_0 )}{t}} = \frac{ \partial f}{ \partial y} (x_0 , y_0 )$$
2) Uma função pode ser contínua num ponto, ter derivada direcional em todas as direções neste ponto, e mesmo assim não ser diferenciável neste ponto.
Interpretação Geométrica da Derivada Direcional
Observe que a derivada direcional de uma função f(x,y) numa direção do vetor unitário \vec{u} = (a,b) num ponto (x_0, y_0) , é o declive da curva interseção da superfície z = f(x,y) com o plano que passa por (x_0, y_0) e é paralelo ao eixo Oz e à direção \vec{u} = (a,b) , cuja equação é $$(x-x_0) a – (y – y_0 ) b = 0 .$$
Sendo \psi o ângulo dessa interseção com o plano horizontal x0y , isso significa que $$ \frac{ \partial f}{ \partial \vec{u}} (x_0 , y_0) = tg ( \psi) . $$
Como \vec{u} = (a,b) é unitário, se \nabla f (x_0 , y_0) \neq \vec{0} , podemos escrever a fórmula $$ D_{\vec{u}} f = \nabla f . \vec{u} = \| \nabla f \| cos \theta , $$ onde \theta é o ângulo entre os vetores \nabla f e \vec{u}.
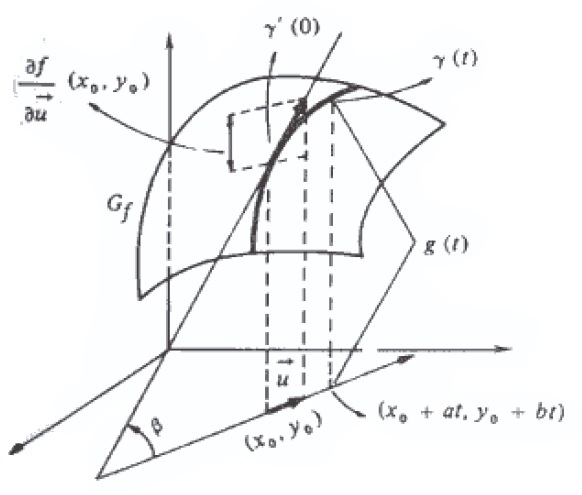 Interpretação geométrica da Derivada Direcional
Interpretação geométrica da Derivada Direcional
O Gradiente e a Derivada Direcional
Se f for diferenciável em (x_0, y_0) , então f admitirá derivada direcional em todas as direções, no ponto (x_0, y_0) , e cada derivada direcional se exprime de modo bastante simples em termos do gradiente de f em (x_0, y_0) .
Pode-se mostrar que se \vec{u} = (a,b) é um vetor unitário e f for diferenciável em (x_0, y_0) , então $$ \frac{ \partial f}{ \partial \vec{u}} (x_0 , y_0) = \nabla f (x_0 , y_0) . \vec{u} = a \frac{ \partial f}{ \partial x} (x_0 , y_0 ) + b \frac{ \partial f}{ \partial y} (x_0 , y_0 ) .$$
Além disso, sob essas condições, se \nabla f (x_0 , y_0) \neq \vec{0} então podemos afirmar que o valor máximo de \dfrac{ \partial f}{ \partial \vec{u}} (x_0 , y_0) ocorre quando \vec{u} = \dfrac{\nabla f (x_0 , y_0)}{\| \nabla f (x_0 , y_0) \|} e esse valor de máximo é exatamente \| \nabla f (x_0 , y_0) \| .
Ou seja, estando em (x_0, y_0) , a direção e sentido que se deve tomar para que f cresça mais rapidamente é a do vetor \nabla f (x_0 , y_0) .
Ainda podemos afirmar que a derivada direcional é zero quando a direção \vec{u} é perpendicular à direção do gradiente.
EXEMPLO
Vamos calcular \frac{ \partial f}{ \partial \vec{u}} (1,2) , onde f(x,y) = x^2 + xy e \vec{u} = (a,b)
Neste caso, como f é diferenciável, $$ \frac{ \partial f}{ \partial \vec{u}} (1,2) = \nabla f (1,2) . \vec{u} = a \frac{ \partial f}{ \partial x} (1 , 2 ) + b \frac{ \partial f}{ \partial y} (1 , 2 ) .$$
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Como $$ \frac{ \partial f}{ \partial x} (x,y ) = 2x +y $$ $$\frac{ \partial f}{ \partial y} (x,y ) = x, $$ então $$\nabla f (1,2) = (4,1).$$
Portanto, $$ \frac{ \partial f}{ \partial \vec{u}} (1,2) = 4a +b .$$
EXEMPLO
Seja f(x,y) = x^2 y .
Desta forma, facilmente encontramos \nabla f (1,1) = (2,1).
Como essa função é diferenciável no ponto (1,1) e \nabla f (1,1) \neq (0,0) , segue que \frac{ \partial f}{ \partial \vec{u}} (1,1) é máximo para $$ \vec{u} = \frac{\nabla f (1,1)}{\| \nabla f (1,1) \|} = \left( \frac{2}{\sqrt{5}} , \frac{1}{\sqrt{5}} \right) . $$
Além disso, o valor de máximo que \frac{ \partial f}{ \partial \vec{u}} (1,1) assume é $$ \| \nabla f (1,1) \| = \sqrt{5}. $$
Além disso é importante lembrar que \nabla f (1,1) = (2,1). aponta a direção e sentido em que f cresce mais rapidamente (1,1).
A Derivada Direcional Para Funções de Três Variáveis
É claro que as mesmas ideias abordadas se aplicam no caso de funções de três ou mais variáveis independentes.
Sendo \vec{u} = (a,b,c) um vetor unitário no \mathbb{R} ^3 , a derivada de uma função diferenciável w = f(x,y,z) na direção de \vec{u} é dada por $$\frac{\partial f}{\partial \vec{u}} = \nabla f . \vec{u}. $$
A fórmula $$ D_{\vec{u}} f = \nabla f . \vec{u} = \| \nabla f \| cos \theta, $$ onde \theta é o ângulo entre os vetores \nabla f e \vec{u}, permanece válida neste caso.
Exercícios Resolvidos
Leia Mais:
- Derivadas Parciais | Funções de Várias Variáveis a Valores Reais
- O que é o Vetor Gradiente? | Funções de Várias Variáveis
- A Diferencial | Funções de Várias Variáveis a Valores Reais
- Diferenciabilidade | Funções de Várias Variáveis a Valores Reais


