No espaço \mathbb{R}^3, considere P(x,y,z) um ponto de um conjunto de pontos do espaço. Se para cada ponto P deste conjunto associarmos um vetor \vec{F}(P) = \vec{F}(x,y,z), então obtemos um campo vetorial para estes pontos e \vec{F}(x,y,z) é denominada função vetorial.
Em coordenadas cartesianas, $$\vec{F}(x,y,z) = F_1(x,y,z) i + F_2(x,y,z)j + F_3(x,y,z)k$$ onde i = (1,0,0), j = (0,1,0) e k = (0,0,1) e F_i : \mathbb{R}^3 \rightarrow \mathbb{R}
Curvas de Fluxo ou Curvas Integrais do Campo Vetorial
Se \vec{F} é um campo vetorial contínuo, \gamma é uma curva do fluxo de \vec{F} se $$\gamma ‘ (t) = \vec{F}( \gamma (t)).$$
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
As curvas que formam o fluxo do campo são também chamadas de curvas integrais do campo, pois se \vec{F}(x,y,z) = F_1(x,y,z) \vec{ i } + F_2(x,y,z) \vec{ j } + F_3(x,y,z) \vec{ k } representa a velocidade das partículas num fluido, o movimento do fluido é completamente determinado pelo sistema $$\frac{dx}{dt} = F_1 \left( x(t), y(t), z(t) \right) $$ $$\frac{dy}{dt} = F_2 \left( x(t), y(t), z(t) \right) $$ $$\frac{dz}{dt} = F_3 \left( x(t), y(t), z(t) \right) ;$$ o que nos leva a associar o campo \vec{F} a um sistema de equações diferenciais ordinárias, cuja solução é o fluxo \gamma (t) = \left( x(t), y(t), z(t) \right) de \vec{F}.
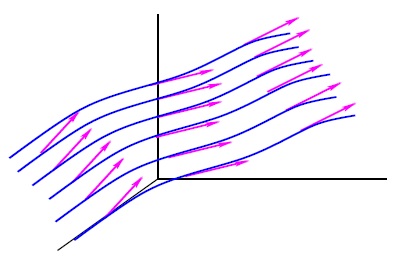 Fluxo do Campo Vetorial
Fluxo do Campo Vetorial
EXEMPLO (A Equação do Pêndulo Plano)
Considere o campo vetorial gerado pela equação diferencial ordinária que modela o pêndulo plano: $$\frac{d^2 x}{dt} + \frac{g}{L} sen(x) = 0,$$ onde L é comprimento da haste que sustenta uma massa m e g é a gravidade.
Esta equação pode ser reescrita como $$ \frac{dx}{dt} = y(t)$$ $$\frac{dy}{dt} = – \frac{g}{L} sen(x),$$ ou seja, o campo vetorial das soluções desta equação é dado por $$ \vec{F} (x,y) = \left( y , – \frac{g}{L} sen(x) \right)$$ e este campo é denominada plano de fase ou retrato de fase da EDO, que neste caso é dado abaixo:
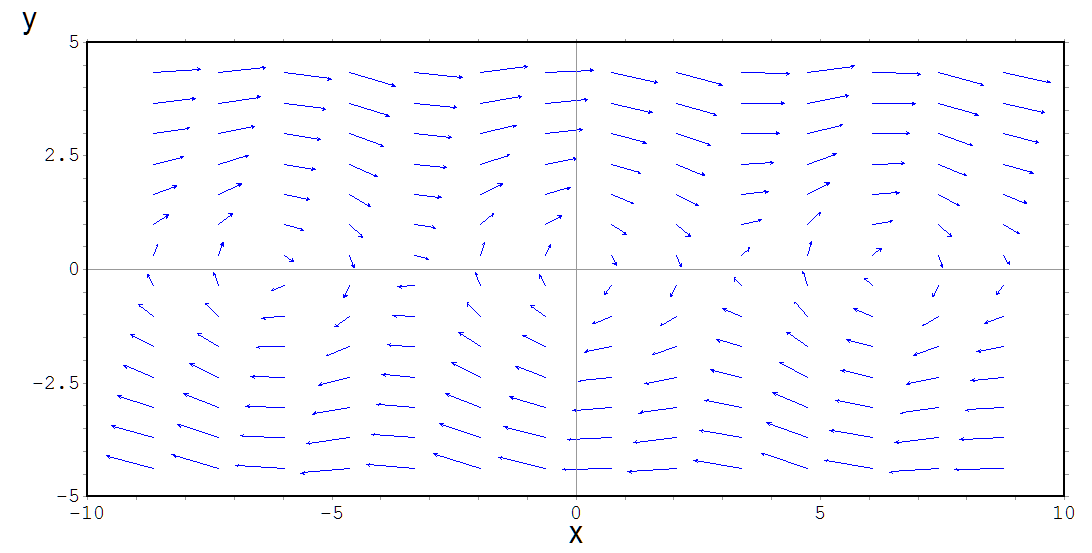
As curvas de fluxo deste campo vetorial que formam o plano de fase da equação diferencial são as representações gráficas das soluções da EDO.
Neste caso, as curvas são dadas por $$ \gamma (t) = \left( t, \pm \sqrt{2k + \frac{2g}{L} \cos(t)} \right),$$ onde k é a constante associada ao ponto do plano por onde cada curva passa.
Estas curvas de fluxo do campo vetorial são representadas graficamente pela imagem abaixo:
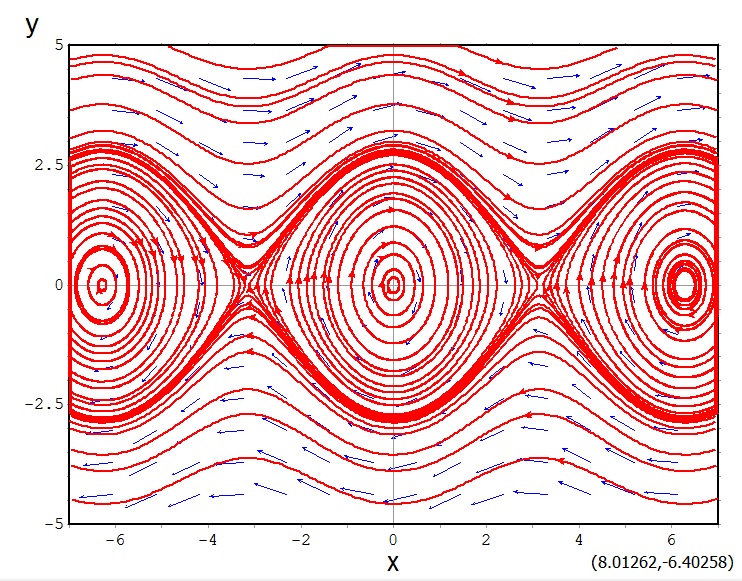 Plano de fase do pêndulo plano
Plano de fase do pêndulo plano
EXEMPLO (Encontrando o Fluxo de um Campo Vetorial)
Considere o campo vetorial gerado por \vec{F} (x,y) = \left( x , - y \right) .
Desta forma as curvas de fluxo estão associadas ao sistema de equações diferenciais: $$\frac{dx}{dt} = x$$ $$\frac{dy}{dt} = -y.$$
Este é um sistema de variáveis desacopladas o que permite a solução de cada equação separadamente.
Para solucionar \dfrac{dx}{dt} = x precisamos encontrar uma função que seja igual à sua própria derivada. Desta forma, podemos escrever $$x(t) = c_1 e^t .$$
Por um raciocínio análogo, podemos dizer que $$y(t) = c_2 e^{-t},$$ afinal uma função que seja igual à sua própria derivada multiplicada por -1 soluciona a equação \dfrac{dy}{dt} = -y .
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Portanto, as curvas de fluxo do campo \vec{F} (x,y) = \left( x , - y \right) são dadas por
$$ \gamma (t) = \left( c_1 e^t, c_2 e^{-t} \right),$$ que são equivalentes às curvas planas dadas pela relação $$y = \frac{c}{x},$$ onde c = c_1 \times c_2 .
O campo vetorial e as curvas de fluxo são representadas graficamente abaixo:

EXEMPLO (O Fluxo do Campo Radial de Quadrado Inverso)
O fluxo do campo quadrado inverso é dado por $$ \gamma (t) = \sqrt[3]{k t} \vec{u} $$ onde \vec{u} \in \mathbb{R}^3 é um vetor unitário fixo.
Listas de Exercícios Resolvidos
Leia Mais:
- Campos Vetoriais Conservativos e Potencial
- Campo Vetorial | O que são as Curvas de Fluxo ou Curvas Integrais?
- O Rotacional de um Campo Vetorial | Definição e Interpretação Geométrica
- O Divergente de um Campo Vetorial | Definição e Interpretação
- Integral de Linha de 1ª e 2ª Espécies, e o Teorema de Green no Plano



Pingback: Campos Vetoriais | 1ª Lista de Exercícios Resolvidos
Pingback: O Rotacional de um Campo Vetorial | Definição e Interpretação Geométrica - Matemática Simplificada
Pingback: O Divergente de um Campo Vetorial | Definição e Interpretação
Pingback: Campos Vetoriais | 2ª Lista de Exercícios Resolvidos
Pingback: Campo Radial de Quadrado Inverso | Campos Vetoriais