Funções Afim, Quadrática e Polinomiais | Funções Reais (Pré-Cálculo)

Uma função polinomial é aquela que associa uma variável a um polinômio de grau n . A forma geral de uma função polinomial é dada por $$f(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + … + a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0 ,$$ onde n \in \mathbb{N} e cada um dos números reais a_i com i = 1,2,3,4,..., n são denominados coeficientes.

Cada termo a_i x^i é chamado de monômio, assim, funções na forma f(x) = a_n x^n são chamadas de monomiais. Ou seja, funções polinomiais são apenas somas finitas de funções monomiais na variável x . Além disso, o domínio de toda função polinomial é o conjunto dos números reais.

O grau de um polinômio é o máximo grau observado entre os graus de seus monômios e o coeficiente do monômio de grau máximo é chamada do coeficiente dominante do polinômio. desta forma, a função afim é polinomial de grau, a função quadrática é polinomial do segundo grau e são exemplos de funções polinomiais de graus três: f(x) = x^3, f(x)= x^3 + x^2 + x e f(x) = x^3-3x^2+2x .

OBSERVAÇÃO: Muito cuidado com funções como as exemplificadas elas não são polinômiais, pois respectivamente, possuem um expoente fracionário e um expoente negativo:

1. f(x) = x + x^{1/2}+2 ;
2. g(x) = -1 + 2x + x^{-3} .

A Função Afim (ou do 1º Grau)

Uma função real f:\mathbb{R} \rightarrow \mathbb{R} dada por f(x) = ax+b, onde a e b são números reais e a\neq 0 é denominada Função Afim. Por vezes ela é também chamada de Função do 1° grau, mas esta referência é errada, pois função não tem grau, polinômio sim. Talvez pela associação com polinômios do primeiro graus está nomenclatura tenha se aplicado. Uma função afim é denominada linear se for do primeiro grau e b=0.

O domínio de uma função afim é conjunto dos números reais, assim como a imagem corresponde ao mesmo conjunto. Existe um elemento do domínio muito importante chamado de raíz da função afim, que o valor cuja imagem é zero. A função afim sempre possui raíz que é encontrada fazendo $$f(x) = 0 \Leftrightarrow ax+b = 0 \Leftrightarrow x=\frac{-b}{a}.$$

O gráfico de uma função afim é sempre uma reta crescente se a>0 ou uma reta decrescente se a<0. a = \tan{\alpha} é denominado coeficiente angular e b é denominado coeficiente linear.

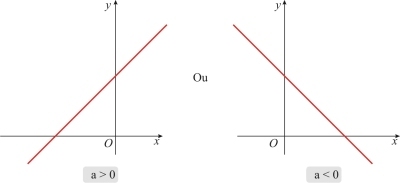
EXEMPLO: As funções f(x) = 2x+3 e g(x) = -5x+4 são exemplos de funções afim.

EXEMPLO: Vamos determinar a função afim cujo gráfico passa por A(-2,10) e B(1,4). De modo simples podemos dizer que a função afim que passa pelos pontos indicados tem natureza na forma $$y = ax+b.$$ Desta forma, temos o sistema $$ 10 = -2a + b $$ $$4 = a +b.$$ Da segunda linha temos que b = 4-a e substituindo na primeira linha, obtemos $$ 10 = -2a +(4-a) = -3a +4 \Leftrightarrow a = – \frac{6}{3} =- 2 ,$$ daí $$ b  = 4 – a = 4 –  \left( – 2\right) = 6.$$ Portanto, a nossa função é dada por $$y = – 2 x + 6.$$

EXEMPLO: Vamos determinar m e n para que g(x) = (m-2)x^2 + 4x+n+6 seja linear. Neste caso, de modo simples observamos que $$m-2 = 0$$ $$n+6=0$$ são as condições para que a função seja linear. Logo, basta que m = 2 e n = -6

A Função Quadrática (ou do Segundo Grau)

A função f(x) = ax^2+bx+c, a \neq 0 é chamada de função do 2º grau. Seu domínio é o conjunto dos números reais.

As raízes da equação do segundo grau

Para investigar as raízes de uma equação do segundo grau utilizamos a conhecida Fórmula de Bháskara. Queremos encontrar valores para a variável x de modo que $$f(x) = ax^2+bx+c=0.$$

O DISCRIMINANTE: Denotado por \Delta = b^2-4ac, nos diz quantas raízes reais reais possui aquela equação do seungo grau:

1. Se \Delta <0, a equação não possui raíz real;
2. Se \Delta = 0, a equação possui uma raíz real com multiplicidade 2
3. Se \Delta >0 a equação possui duas raízes reais distintas.

Para determinar efetivamente as raízes solucionamos a equação: $$x=\frac{-b\pm \sqrt{\Delta}}{2a}.$$

O Gráfico de uma equação do 2º Grau:

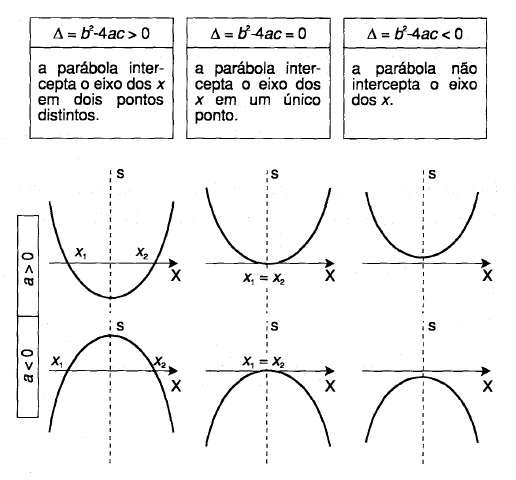
O Vértice da Parábola

O vértice dá parábola que o gráfico da função quadrática é dado pelo par ordenado $$\left( \frac{-b}{2a}, \frac{-\Delta}{4a} \right).$$ Além disso, a este vértice é ponto de máximo global da função se a concavidade da parábola for para baixo e ponto de mínimo global da função se a concavidade da parábola for para cima.

Tópicos Sobre Polinômios

Agora, queremos desenvolver alguns tópicos sobre polinômios que podem ajudar no estudo das funções polinomiais. Considerando $$p(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + … + a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0 ,$$

1. Seja \alpha um número real, o valor numérico de p(x) em \alpha é o valor obtido quando substituímos x por \alpha e efetuamos as operações indicadas, ou seja, o valor numérico de uma função polinomial é sua imagem em dado ponto do domínio.
2. Quando p( \alpha ) = 0 dizemos que \alpha é raíz da função polinomial.
3. Se \lambda _i é a multiplicidade da raiz \alpha _i (ou seja quantas vezes esta raíz aparece), então o polinômio p(x) pode ser decomposto como $$ p(x) = \prod\limits_{i = 1}^{r}{(x – \alpha _i) ^{\lambda _i}}= (x – \alpha _1) ^{\lambda _1} \times (x – \alpha _2) ^{\lambda _2} \times (x – \alpha _3) ^{\lambda _3} \times  … \times (x – \alpha _r) ^{\lambda _r} $$ onde \lambda _1 + \lambda _2 + \lambda _3 + ... + \lambda _r = n . Esta definição é única e cada termo do produto é denominado fator do polinômio.
4. Obviamente um polinômio é sempre divisível por cada um de seus fatores.
5. Polinômios definidos por variáveis reais admitem decomposição em termos de polinômios de grau 1 e grau 2 irredutíveis (que não admitem raízes reais).
6. Polinômio nulo ou polinômio identicamente nulo é aquele que tem todos os coeficientes iguais a zero e indicamos p(x) = 0 .
7. Dois polinômios são iguais quando todos os seus coeficientes são ordenadamente iguais.
8. Se os coeficientes da função polinomial p(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + ... + a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0 são todos números inteiros e o número racional \dfrac{p}{q} , onde p e q \neq 0 são inteiros primeiro entre si, é raíz desta função, então p é divisor de a_0 e q é divisor de a_n .

As Relações de Girard

Algumas relações entre os coeficientes de uma equação e sua raízes, conhecidas como relações de Girard, constituem uma ferramenta importante para encontrar raízes de funções polinomiais com grau maior do que 2. Considerando p(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + ... + a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0, com a_n \neq 0  e r_1 , r_2 , ... r_n as raízes de p(x) . Então:

\begin{equation} \left\{ \begin{array}{l} r_1 + r_2 + … + r_n = – \frac{a_{n-1}}{a_n} \\ r_1 \cdot r_2 + r_1 \cdot r_3 + … + r_{n-1} \cdot r_n =  \frac{a_{n-2}}{a_n} \\ r_1 \cdot r_2 \cdot r_3 + r_1 \cdot r_2 + r_1 \cdot r_4 + … + r_{n-2} \cdot r_{n-1} \cdot r_n = – \frac{a_{n-3}}{a_n} \\ \vdots \\ r_1 \cdot r_2 \cdot r_3 \cdot  … \cdot  r_n = (-1)^n \frac{a_{0}}{a_n} \end{array} \right. \end{equation}

Observe que a primeira linha das relações de Girard traz a soma das n raízes, a segunda linha traz a soma dos produtos das raízes tomadas duas a duas, a terceira linha traz a soma dos produtos das raízes tomadas três a três e assim sucessivamente até a última linha que traz o produto das n raízes.

EXEMPLO (A Função Polinomial do 3º Grau): A função polinomial na forma $$p(x) = ax^3 + bx^2 +cx +d $$ é uma função polinomial do terceiro grau, pois associa uma variável real a uma polinômio de grau 3.

Uma função de domínio real e até três raízes reais e distintas e que satisfazem as relações de Girard: \begin{equation} \left\{ \begin{array}{l} r_1 + r_2 +r_1 = – \frac{-b}{a} \\ r_1 \cdot r_2 + r_1 \cdot r_3 + … + r_{2} \cdot r_{3} =  \frac{c}{a} \\ r_1 \cdot r_2 \cdot r_3 = – \frac{d}{a} \end{array} \right. \end{equation}

Geralmente, quando encontramos uma raíz real da função polinomial cúbia, a decompomos como $$p(x) = (x- \alpha) (Ax^2 + Bx +C)$$ e verificamos se o polinômio do segundo grau possui raízes reais. Caso contrário esta será sua decomposição.

O Método de Cardano-Tartaglia garante a existência de pelo menos uma solução real dada pela fórmula $$ x_{real} = – \frac{b}{3a} + \sqrt[3]{-\frac{q}{2}  + \sqrt{\frac{q^2}{4} + \frac{p^3}{27} } } + \sqrt[3]{-\frac{q}{2}  – \sqrt{\frac{q^2}{4} + \frac{p^3}{27} } } $$ onde $$p = \frac{c}{a} – \frac{b^2}{3a^2} \qquad q = \frac{d}{a} – \frac{bc}{3a^2} + \frac{2b^3}{27 a^3}.$$

Leia Mais:

• Introdução à Teoria dos Conjuntos | Pré Cálculo
• Pré-Cálculo: Teoria dos Conjuntos | Lista de Exercícios Resolvidos
• Números Reais | Definição, Operações Elementares, Intervalos e Módulo
• Pré-Cálculo: Números Reais | 1ª Lista de Exercícios Resolvidos