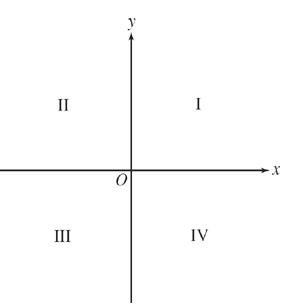
Na Geometria Analítica, o sistema de coordenadas polares é um sistema de coordenadas bidimensional no qual os pontos do plano cartesiano são dados por um ângulo e uma distância de um ponto central conhecido como origem (ou polo).
integrais duplas, que definimos neste artigo
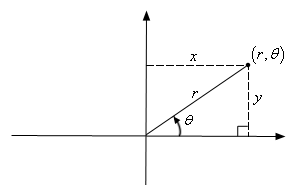Equivalência entre os sistemas de coordenadas cartesianas e polares.
| Quadrante | Coordenadas Cartesianas | Amplitude Ângular |
|
| I | (x,y) | 0 < \theta < \dfrac{ \pi}{2} | |
| II | (-x,y) | \dfrac{ \pi}{2} < \theta < \pi | |
| III | (-x,-y) | \pi < \theta < \dfrac{ 3 \pi}{2} | |
| IV | (x,-y) | \dfrac{3 \pi}{2} < \theta < 2 \pi |
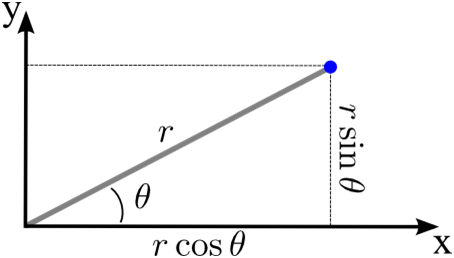
Fórmula de Coordenadas Polares
Relação entre Coordenadas Cartesianas e Coordenadas Polares
EXEMPLO: Solução:
EXEMPLO: Solução:
EXEMPLO:
EXEMPLO:
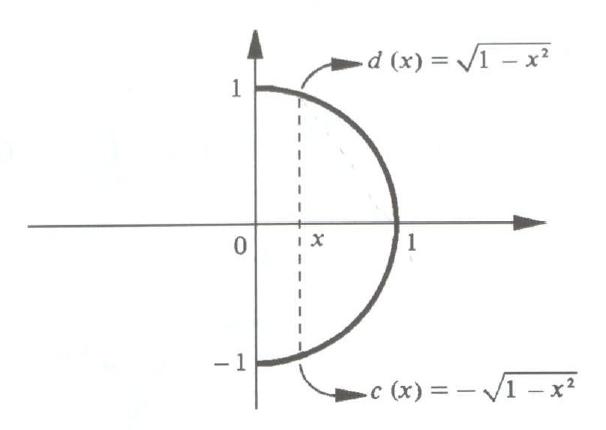
Para escrever esta região no plano em termos das coordenadas cartesianas, temos que
$$R: \left\{ \begin{array}{l}
0 \leq x \leq 1\\
-\sqrt{x^2+y^2}\leq y \leq \sqrt{x^2 + y^2}
\end{array} \right.$$
Fazendo x=r\cos{\theta} e r\sin{\theta}, escrevos esta região como $$R: \left\{ \begin{array}{l}
0 \leq r \leq 1\\
-\pi/2\leq \theta \leq \pi/2
\end{array} \right.$$
EXEMPLO: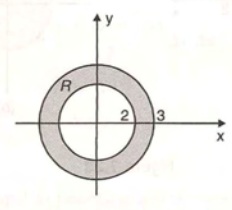 
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
EXEMPLO:
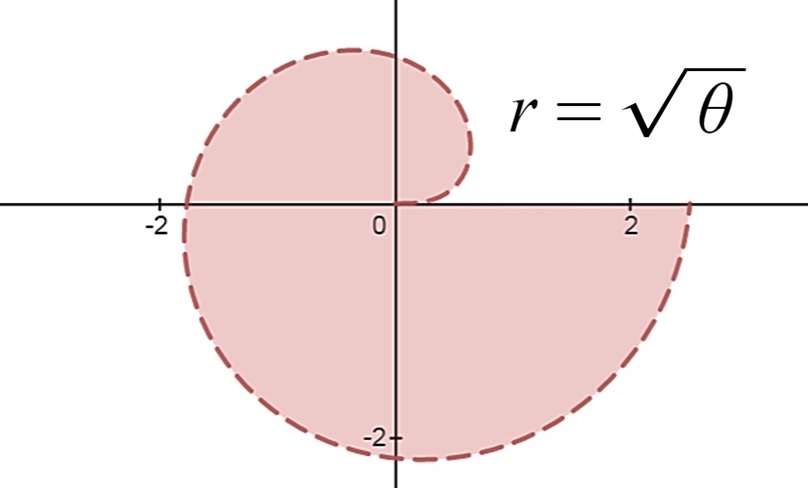
EXEMPLO:
Leia Mais:
- A Circunferência: Equações, Posições Relativas e Retas Tangente e Secante
- Compreendendo as Seções Cônicas: Um Guia Introdutório
- Coordenadas Polares e a Mudança de Variável nas Integrais Duplas
- Números Complexos | A Forma Polar e as Operações Elementares
