Um conjunto é uma palavra para designar uma coleção de objetos, e eles são sempre indicados por letras maiúsculas. Já os objetos de um conjunto são denominados elementos e são indicados por letras minúsculas. Como toda a matemática moderna é apresentada na linguagem dos conjuntos, o cálculo diferencial e integral não foge à regra.
Alguns tipos de conjuntos são especiais no estudo da matemática. O conjunto unitário, por exemplo, é aquele que apresenta somente um elemento. Já o conjunto que não possui nenhum elemento é conhecido como conjunto vazio e é indicado pelo símbolo \emptyset . Por conjunto universo entendemos aquele conjunto ao qual pertencem todos os elementos e dois conjuntos só serão iguais quando todo elemento de um pertence ao outro.
Relações de Pertinência
A relação básica entre um objeto e um conjunto é a relação de pertinência. Um conjunto fica definido (determinado, ou caracterizado) quando se dá uma regra que permita decidir se um objetos arbitrário pertence ou não a ele. Até por isso, primeiramente, vamos tratar das relações de pertinência entre os elementos e os conjuntos. Para isto utilizamos os símbolos:
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
- \in (pertence): isso quer dizer que o elemento está no conjunto;
- \notin (não pertence): isso quer dizer que o elemento não está no conjunto.
Dizemos que a pertence à um conjunto A se a é um elemento de A e indicamos esta relação por $$a \in A.$$ Caso contrário, se a não pertence ao conjunto A, então utilizamos a seguinte notação para esta relação $$a \notin A.$$
Você pode definir um conjunto apenas listando seus objetos entre chaves como abaixo:
- A = \{1, 3, 5, 7, 9\} ;
- V = \{a, e, i, o, u\};
- F = \{laranja, \; banana, \; abacaxi\};
- \mathbb{N}=\{1,2,3,4,5,6,7,8,...\};
- \mathbb{Z}=\{...,-3,-2,-1,0,1,2,3,...\}.
Entretanto, a maioria dos conjuntos encontrados no estudo do cálculo não são definidos especificando-se um a um seus elementos. Por exemplo, podemos definir o conjunto A dos triângulos retângulos como o formado por todos os triângulo de lados a , b e c que possuem um ângulo reto.
O método mais frequente de definir um conjunto é por meio de uma propriedade comum e exclusiva dos seus elementos. Geralmente, utilizamos a forma $$A = \{x \,:\, P(x)\},$$ onde P(x) representa uma propriedade comum a todos os elementos do conjunto. Nestas condições, definimos o conjunto vazio como $$ \emptyset = \{ x ; x \notin \emptyset \}$$ ou então $$ \emptyset = \{ x ; x \neq x \}.$$
Ou seja, Um conjunto A fica definido quando se dá uma regra que permita se decidir se um objeto arbitrário x pertence ou não a A . Por exemplo, considere o conjunto \mathbb{N} e a propriedade P: “x é maior do que 5″. Esta propriedade define o conjunto $$A=\{ x \in \mathbb{N}; x > 5\}=\{6,7,8,9,10…\}.$$
O conjunto dos números racionais pode ser escrito desta forma. Podemos definir o conjunto $\mathbb{Q}$, dos números racionais, utilizando $$\mathbb{Q}= \left\{ \frac{p}{q}; \; p,q \in \mathbb{Z},\;\;\; q \neq 0\;\;\; e \;\;\; mdc(p,q)=1\right\}.$$
Relações de Inclusão e Subconjuntos
Outra relação inerente aos conjuntos são as relações de inclusão. Esta relação envolvem conjuntos e para designá-las utilizamos os seguinte símbolo: \subset, que significa está contido.
Dizemos que um conjunto A esta contido num conjunto B se todo elemento de A é um elemento de B. Denotamos esta relação por $$A \subset B.$$
Podemos, então, definir o que é um subconjunto. O conjunto A será um subconjunto de B se A \subset B. Também podemos dizer que A é parte de B, que A está incluído em B, ou contido em B. Os conjuntos numéricos, por exemplo, obedecem à cadeia de inclusão: $$ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}.$$
A relação de inclusão A\subset B satisfaz as propriedades:
- Reflexiva: A\subset A , seja qual for o conjunto A ;
- Anti-Simétrica: Se A\subset B e B \subset A , então A = B (ou seja, od dois conjuntos possuem os mesmos elementos, sendo, portanto, o mesmo conjunto); e
- Transitiva: se A\subset B e B\subset C , então A\subset C .
Uma conclusão óbvia, mas altamente pertinente, diz que para mostrar que um conjunto A não está contido em um conjunto B basta mostra que um elemento de A que não está em B.
A relação de pertinência ainda implica na existência do conjunto das partes de um conjunto A, que é o conjunto formado por todos os subconjuntos de A. Mas que para o nosso objetivo introdutório se torna um tanto profundo e por isso deixaremos este tema para os futuros artigos de Análise Real.
União e Interseção
Dados dois conjuntos A e B, podemos criar um “novo” conjunto formado pelos elementos de A e pelos elementos de B. Este conjunto é formado pela UNIÃO de A com B. Se este novo conjunto é denominado C, denotamos a união por $$C=A\cup B = \left\{x; x\in A\;\;\;ou\;\;\;x\in B\right\}.$$
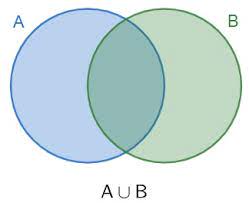 União de dois conjuntos.
União de dois conjuntos.
Analogamente, podemos criar outro conjunto, geralmente diferente do construído com a união, formado pelos elementos que estão tanto em A quanto a B. Este conjunto, denotado por $$A\cap B = \left\{x; x\in A\;\;\;e\;\;\;x\in B\right\}$$, é denominado interseção de A com B. Dois conjuntos são ditos disjuntos se A \cap B = \emptyset .
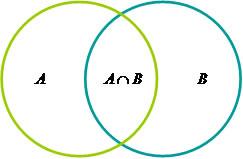 Interseção de dois conjuntos.
Interseção de dois conjuntos.
EXEMPLO: Se A=\left\{ 1,2\right\} e B=\left\{ 1,5,6\right\}, então:
- A\cup B = \left\{1,2,5,6\right\}
- A\cap B = \left\{1\right\}
Parecem implicações óbvias, mas é necessário o registro de que, independente de quais forem os conjuntos A e B , tem-se sempre
- A\subset A \cup B e B\subset A \cup B ;
- A \cap B \subset A e A \cup B \subset B .
Além disso, abaixo listamos as principais propriedades formais das operações de reunião e interseção:
| União | Interseção |
| A \cup \emptyset = A | A \cap \emptyset = \emptyset |
| A \cup A = A | A \cap A = A |
| A \cup B = B \cup A | A \cap B = B \cap A |
| (A \cup B) \cup C = A \cup (B \cup C | (A \cap B) \cap C = A \cap (B \cap C |
| A \cup B = A \Leftrightarrow B \subset A | A \cap B = A \Leftrightarrow A \subset B |
| A \subset B, A' \subset B' \Rightarrow A \cup A' \subset B \cup B' | A \subset B, A' \subset B' \Rightarrow A \cap A' \subset B \cap B' |
| A \cup (B \cap C) = (A \cup B) \cap (A \cup C) | A \cap (B \cup C) = (A \cap B) \cup (A \cap C) |
As demonstrações de qualquer dessas propriedades se reduz ao manejo adequado dos conectivos “e” e “ou”, mas deixaremos suas demonstrações para os artigos sobre Análise Real.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Diferença Entre Conjuntos e o Complementar
A diferença entre os conjuntos A e B é o conjunto $$ A – B = \{ x; x \in A \;\;\; e \;\;\; x \notin B\},$$ ou seja, o conjunto formado pelos elementos de A que não estão em B . Pode se mostrar, conforme ilustrado na figura abaixo, que independente dos conjuntos tomados, $$ A – B = A – (A \cap B) .$$
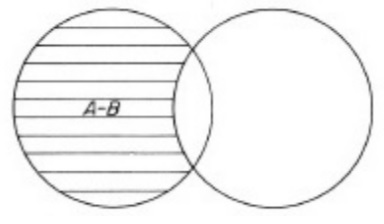 O conjunto A-B
O conjunto A-B
Não se exige que B esteja contido em A para forma a diferençe entre os dois conjuntos. Quando os conjuntos A e B são disjuntos, então A - B = A e B - A = B .
Quando se tem B \subset A , a diferença A - B = A chama-se o complementar de B em relação a A e escrevemos $$ A – B = \mathcal{C}_{A} B .$$
Geralmente em nosso estudo, estaremos considerando um conjunto chamado de conjunto universo, que é aquele que contém todos os conjuntos possíveis na nossa discussão. Para o estudo do cálculo este conjunto será o conjunto \mathbb{R}, dos números reais.
Dado um conjunto A \subset \mathbb{E} a diferença \mathbb{E} - A se chama complementar de A e indicamos apenas pelo símbolo A^C e $$A^C = \{x \in \mathbb{E}; x \notin A\}.$$
Em todo caso, as propriedades e observações sobre o complementar de um conjunto serão deixadas para um futuro artigo mais aprofundado em Análise Real, pois, para o estudo do cálculo esta definição já é o suficiente.



Pingback: Pré-Cálculo: Teoria dos Conjuntos | Lista de Exercícios Resolvidos
Pingback: Funções Afim, Quadrática e Polinomiais | Funções Reais (Pré-Cálculo)