A catenária é uma curva determinada pela forma de uma corrente flexível, de densidade uniforme, suspensa apenas pelas duas extremidades, submetida apenas ao próprio peso. Ela pode ser vista em qualquer fio suspenso em postes de iluminação, por exemplo, e surgiu como problema matemático do “Problema da Corrente Pendente”, sendo que o primeiro a procurar uma solução para o problema foi Galileu Galilei, que a tratou como uma aproximação de uma arco de parábola.
O nome catenária está associado à história do problema, e foi usado pela primeira vez por Christiaan Huygens, cientista holandês que ajudou a dar a primeira expressão analítica para a curva. “Catenária” vem do latim, cadena, que significa corrente ou cadeia, e foi dada pela associação ao problema da corrente.
A catenária tem vasta aplicação na engenharia e arquitetura, pois ela guarda relações com o arco de uso mínimo de material para vencer um determinado vão estrutural. Por isso é amplamente utilizada na construção de arcos arquitetônicos, abóbadas de catedrais, sistemas de distribuição e alimentação elétrica aérea de ferrovias e até iglus.
Você precisa passar em cálculo? Não se preocupe, nós podemos ajudar! Clique aqui e descubra como podemos facilitar sua aprovação. |
A catenária pode ser encontrada em monumentos de cidades pelo mundo, como no Gateway Arch, de St. Louis, nos Estados Unidos, no moderno projeto arquitetônico da Ópera de Sydney, na Austrália, e na Ponte na Rua Senador Feijó, em Santos. Mas não se engane, na maioria dos casos as pontes pênseis assumem a forma de uma parábola, que é diferente da catenária.
Isso se dá pois uma força aplicada em um ponto qualquer da catenária é distribuída igualmente por toda a estrutura, proporcionando maior estabilidade Neste artigo vamos explorar um pouco mais desta curva importante.
A História da Catenária
O primeiro a se dedicar a encontrar uma solução para o problema da catenária foi Galileu, que a tratou como uma forma de parábola, mas em 1669 o matemático e filósofo alemão Joachim Jungius provou que o arco não era uma parábola.
Em 1676, o cientista inglês Robert Hooke mostrou que a forma da catenária tinha uma relação a do arco com uso mínimo de material para vencer determinado vão estrutural no artigo “A description of helioscopes and some other instruments“, em resposta ao matemático e arquiteto inglês Christopher Wren que pedia por regras universais a respeito da estrutura dos arcos e suas formas.
Porém, o problema de estabelecer uma expressão analítica para a catenária ainda estava em aberto, com Jakob Bernoulli propondo na Acta Eruditorum, uma revista científica alemã, fundada em Leipzig por Otto Mencke, e publicada mensalmente entre 1682 e 1782, o problema da “curva formada por um fio pesado, flexível, inextensível, e de densidade constante em todo o seu comprimento, suspenso nos seus extremos.”
A proposta de Bernoulli era encontrar uma expressão analítica para a catenária. Formulado em 1690, o problema fora solucionado por Leibiniz naquele mesmo ano, porém, a solução não fora publicada. No ano seguinte, a primeira solução é publicada na própria Acta Eruditorum por Johann e Jakob Bernoulli, além de Huygens.
Em 1697, o matemático e astrônomo escocês David Gregory publicaria um tratado dedicado exclusivamente às catenárias.
A Construção da Catenária com Régua e Compasso.
- No eixo cartesiano, pegue dois pontos P0 (0, a) e C0 (0, 2a).
- Com o centro do compasso em C0, trace um pequeno arco de P0 a P1.
- Trace a reta que liga C0 ao eixo x, passando por P1, e chame o ponto de encontro com o eixo x Q1.
- Encontre C1 na reta C0Q1 de forma que a distância de Q1 a P1 seja igual à distância de P1 a C1.
- Com o centro do compasso em C1 trace um pequeno arco de P1 a P2.
- Repita o procedimento para achar outros pontos Qi, Pi e Ci.
- A curva ligando os pontos Pi será uma aproximação de uma catenária, enquanto os pontos Ci formam sua evoluta.
- Trace uma linha horizontal e divida-a em segmentos pequenos (quanto menores os segmentos, mais precisa a aproximação).
- Numere as divisões. Trace as retas perpendiculares L1, L3, L5, etc. nos pontos de divisão ímpares.
- Mantendo uma abertura constante para o compasso, trace os arcos C0, C2, C4, etc. com centro nos pontos de divisão pares.
- Escolha um ponto A1 em L1 o mais distante possível de 1 e trace a tangente A1T0 ao arco C0.
- Trace o arco de T0 a T2, T2 no arco C2, com centro em A1.
- Trace a tangente a C2 em T2 e faça-a encontrar L3 em A3.
- Trace o arco de T2 a T4, T4 em C4, com centro em A3.
- Repita o procedimento para achar os pontos Ai e Ti. Os pontos Ai estarão sobre uma catenária, os pontos Ti sobre uma tratriz.
A Expressão e o Comprimento da Catenária
A função que determina a catenária num sistema cartesiano em duas dimensões é dada por $$y = \frac{1}{a} cosh(a x), $$ onde $$a = \frac{\omega _0}{T_0} $$ é a razão entre a tensão no ponto inicial e a densidade linear (peso/unidade de comprimento) da corda.
Além disso, cosh(a x) é uma função hiperbólica definida por $$ cosh(a x) = \frac{1}{2} \left( e^{ax} + e^{-ax} \right).$$
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
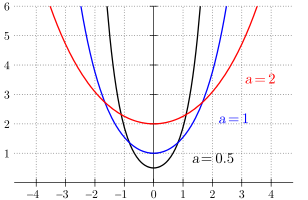 Esboço gráfico da catenária
Esboço gráfico da catenária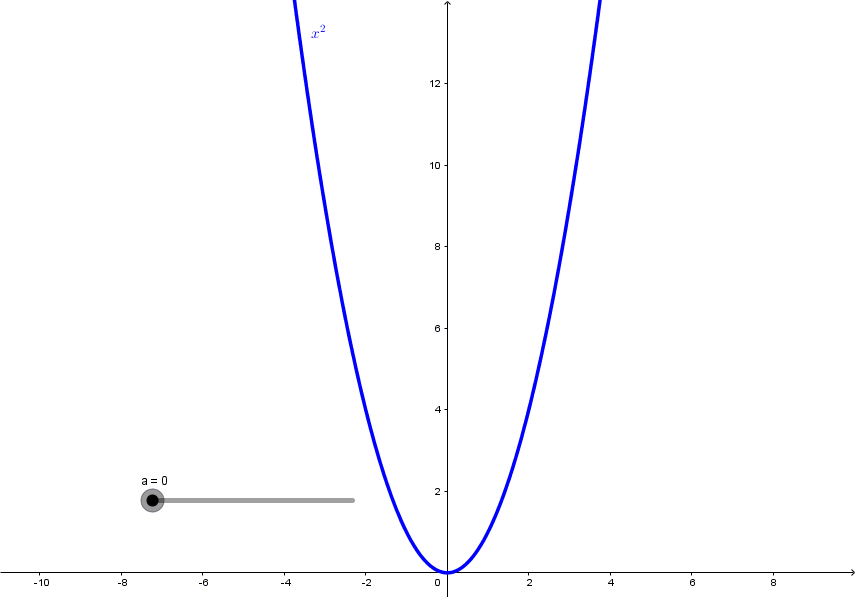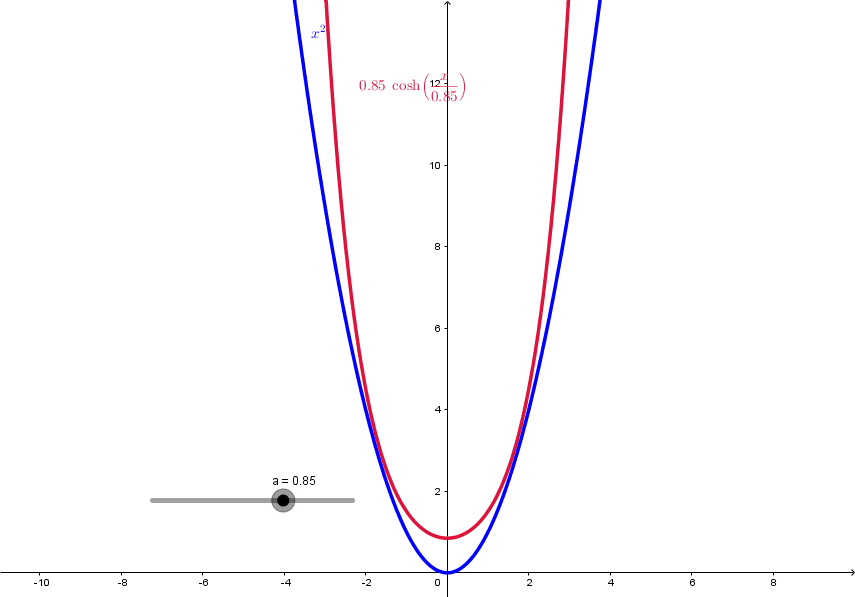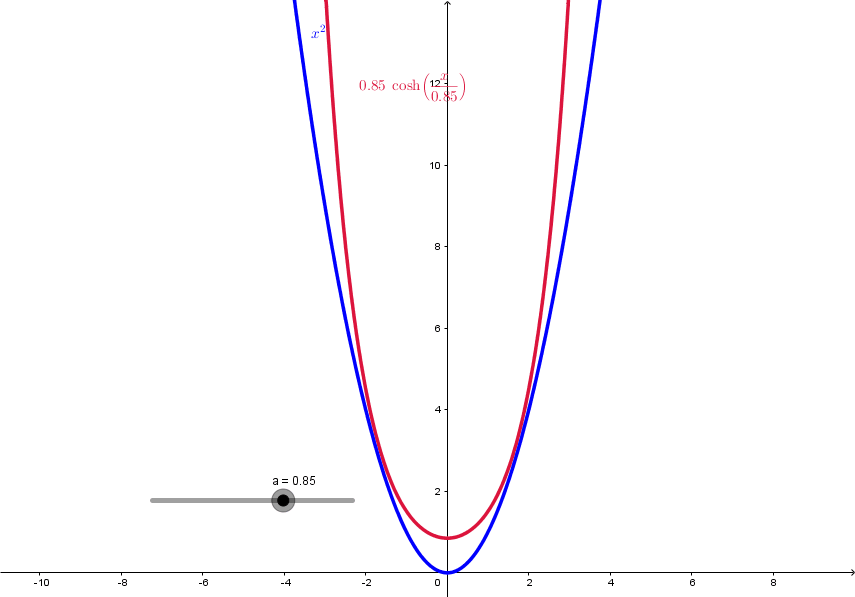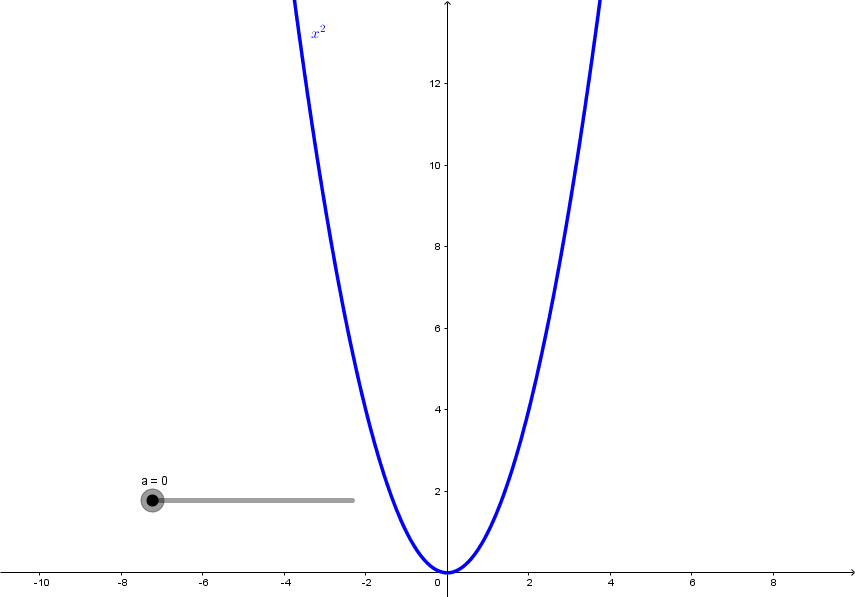 Comparação entre a Catenária e uma Parábola
Comparação entre a Catenária e uma Parábola
Com esta conseguimos calcular o comprimento da catenária apoiada em duas hastes fixas de mesma altura. Para isso, basta lembrar que se a curva plana é representada na forma y = f(x), z = 0 então o comprimento de arco entre x = a e x = b é $$ s = \int_{a}^{b}{\sqrt{1 + (y’)^2}dx}. \tag{1}$$
Desta forma, usando a fórmula (1) e lembrando que cosh' (x) = senh(x) , obtemos $$s = \int_{\alpha}^{\beta}{\sqrt{1 + \left[ \left( \frac{1}{a} cosh(a x) \right)’ \right]^2}dx} = \int_{\alpha}^{\beta}{\sqrt{1 + senh ^2 (ax)}dx}.$$
Lembrando que as funções hiperbólicas satisfazem a relação $$ cosh^2 (ax) – senh^2 (ax) = 1 \Leftrightarrow cosh^2 (ax) = 1 + senh^2(ax),$$ então, usando o fato de que \int{cosh(ax)dx} = \dfrac{senh(ax)}{a} +c, encontramos $$s = \int_{\alpha}^{\beta}{\sqrt{1 + senh ^2 (ax)}dx} = \int_{\alpha}^{\beta}{\sqrt{cosh ^2 (ax)}dx} = $$ $$ = \int_{\alpha}^{\beta}{cosh (ax)dx} = \left[ \frac{senh(ax)}{a} \right]_{\alpha}^{\beta} = \frac{senh(a \beta)}{a} – \frac{senh(a \alpha)}{a}.$$



Pingback: O Fólio De Descartes |